基于三参数小波的频谱分解方法

朱振宇 高佳伦 姜秀娣 孙文博 薛东川 王清振

(中海油研究总院有限责任公司,北京100028； ②中国石油大学(北京),北京 102200)

1 引言

近年来，随着油气勘探工作的不断深入，频谱分解方法已成为油气储层预测中的常用手段。Widess[1]利用楔形模型揭示了薄层反射与薄层厚度的关系。随后，Neidell等[2]引入了调谐厚度的概念，即当层厚为地震子波波长的四分之一时，合成地震记录的振幅最大，此时的地层厚度即为调谐厚度，这是利用地震反射振幅解释薄层厚度的基础。Partyka[3]发现，薄层反射在短时窗傅里叶变换频谱上会出现陷频现象，利用这种现象可以估算薄层厚度；同时，根据地震薄层反射的调谐理论，不同的调谐频率对应不同的薄层厚度[4]，因此通过频谱分解获得的单频体可以反映该频率成分对应的地质现象[5]，挖掘更丰富的信息，还可以突出关键的地质目标，从而提高地震资料的解释精度[6]。

利用频谱分解技术进行地震成像时，需要选择合适的频谱分解方法[7]。Morlet提出的小波变换可以很好地刻画非平稳信号的局部特征，长期以来一直是频谱分解的有力工具[8]。小波变换的效果取决于基小波的选择，由于Morlet小波具有较高的时间、频率分辨率[9]，一直被广泛使用。但是当Morlet小波的中心频率较小时，其修正项就不可忽略。为此，Harrop等[10]提出了一种改进的Morlet小波，该小波在中心频率较小时仍然可以满足小波的允许条件。在Harrop等的研究基础上，高静怀等[11]提出一种灵活性高、具有三个可调参数的三参数小波，主要研究了σ(调制频率)和τ(能量衰减因子)两个参数。

本文研究了三参数小波的每个参数及其参数组合，重点分析了参数β(能量延迟因子)的影响。通过改变参数组合可以获得多种形态的基小波，从而满足不同的处理需求。首先阐述了频谱分解方法的基本原理；然后介绍了三参数小波，重点研究了每个参数对小波的影响；随后设计了正演模型，利用三参数小波进行时频分析；最后利用基于三参数小波的频谱分解方法预测储层，取得了很好的效果。

图1 楔形地质模型及其地震响应特征(a)楔形地质模型； (b)合成地震记录；(c)薄层滤波器的振幅谱；(d)调谐曲线楔形地质模型的盖层和底层具有相同的波阻抗

2 频谱分解方法

频谱分解方法的理论基础来源于薄层反射的调谐现象。由楔形地质模型(图1a)的正演地震记录(图1b)可见，薄层的存在对入射波而言相当于一个滤波器，由薄层滤波器响应的傅里叶振幅谱可以看到周期性频陷现象(图1c)。提取层厚度为25、50ms对应的两条调谐曲线(图1d)，曲线的第一个峰值频率即为该厚度对应的调谐频率，曲线的陷频频率Pf与薄层厚度T(双程旅行时)存在如下对应关系[3]

(1)

利用式(1)就可以计算薄层厚度。

通过上述分析(图1)可知，不同的薄层厚度对应不同的调谐频率，换言之，不同的频率成分包含的地质信息也会有所差异。所以在频谱分解时可分频解释[12](图2)，在不同的单频体上突显关键目标。利用频谱分解可以开展针对性的解释工作，包括刻画砂体的展布和河道的边界等[13-16]，其工作流程如下：

(1)选定目的层段；

(2)选择恰当的时频分析方法进行频谱分解，借助分频处理手段获得离散的单频体；

(3)在每个单频体上制作沿层切片，利用频率切片预测砂体展布、刻画河道边界；

(4)将不同的单频切片进行RGB混色融合，提高储层的解释精度(此步骤可以灵活取舍)。

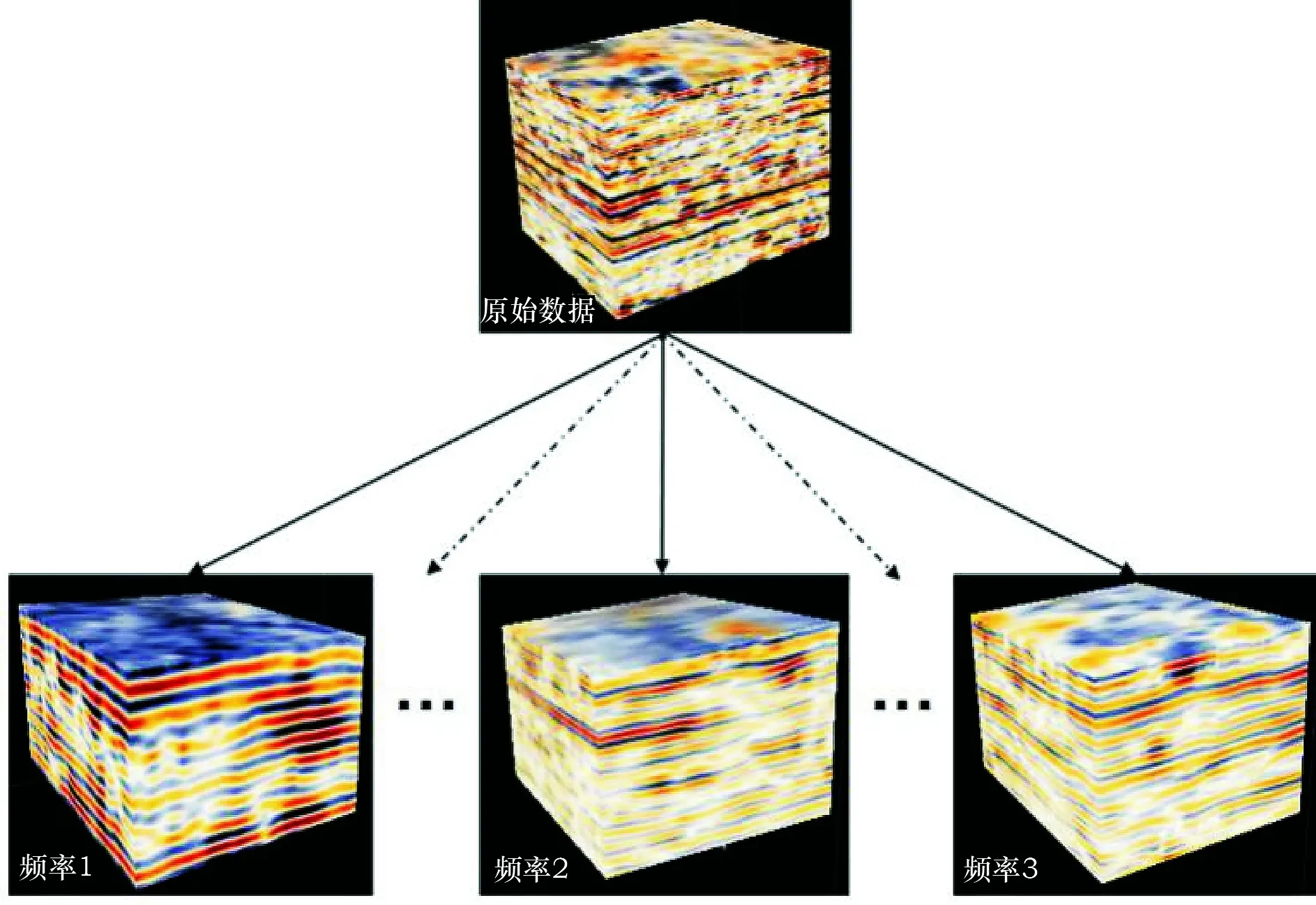
图2 分频解释

3 三参数小波变换

在频谱分解时需要选择合适的时频分析方法。目前已发展的时频分析方法种类繁多[17]，小波变换是其中的一种方法。20世纪80年代初期，Grossmann 等[18]发现传统的傅里叶变换在分析地震信号的局部特征时遇到了瓶颈，无法刻画信号在某种频率出现的时间位置。为此，引入小波变换的概念弥补这一缺陷。定义信号s(t)的小波变换(WT)为

(2)

式中：ψ(t)为基小波，上角“*”表示取共轭；a≠0为尺度因子；b为平移因子。小波变换的特点是既考虑频率分辨率，也考虑时间分辨率，在分析信号时具有“变焦“功能，可很好地刻画信号的局部特征[19]。小波变换结果与基小波的选择关系紧密[20]。在实际的应用中，Morlet小波具有良好的联合时频分辨率，使用较为广泛。Morlet小波的时间域表达式为

(3)

式中ω0≥5rad/s。由式(3)可以看出，Morlet小波只有一个可调参数，因此在使用时不够灵活。并且当ω0取较小值时，其时域局部化效果不能令人满意。三参数小波可以解决上述问题，其表达式为

ψ(t,Γ)= e-τ(t-β)2{p(Γ)[cos(σt)-k(Γ)]+

iq(Γ)sin(σt)}

(4)

其中

(5)

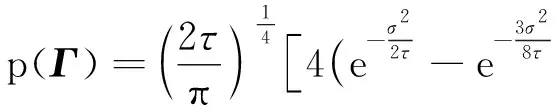
(6)

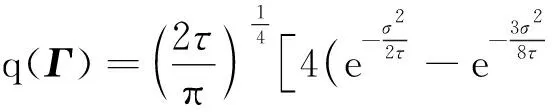
(7)

Γ=(σ,τ,β)

(8)

式中：σ为小波的调制频率；τ为能量衰减因子；β为能量延迟因子[11]。

通过改变三参数小波的3个参数，可以得到不同形态的基小波。因此三参数小波的变化形式多样，选择灵活[21]，可以满足不同的处理需求。下面着重讨论每个参数对小波形态的影响。分析式(4)可以看出，三参数小波是由衰减函数和复变函数相乘得到的，这个复变函数的实部和虚部均为三角函数，而衰减函数相当于一个窗口。所以三参数小波使时间轴上无限分布的函数变为紧支撑集函数，从而符合小波“小”的概念。σ作为调制频率，控制三角函数的频率，影响小波的震荡程度，即σ越大，小波的震荡越剧烈。

图3为不同σ的三参数小波。由图可见，随着σ的不断增大，小波旁瓣增多，震荡加快。τ作为能量衰减因子，控制衰减函数的衰减速度，即τ越大，衰减越快，窗口越窄，小波的波形就越窄。图4为不同τ的三参数小波。由图可见，随着τ的不断增大，小波在时间域的展布变窄，波形变窄。值得注意的是，σ对小波波形的影响程度与τ的取值有关，当τ取值较大(≥3)时，σ对小波的影响变小。这是因为τ较大时，窗口过窄，改变σ，就不易体现小波的周期变化，即震荡程度变化不明显。图5为τ较大时不同σ的三参数小波，与τ较小时不同σ的三参数小波(图3)相比，当τ较大时，改变σ，小波震荡程度变化不明显。

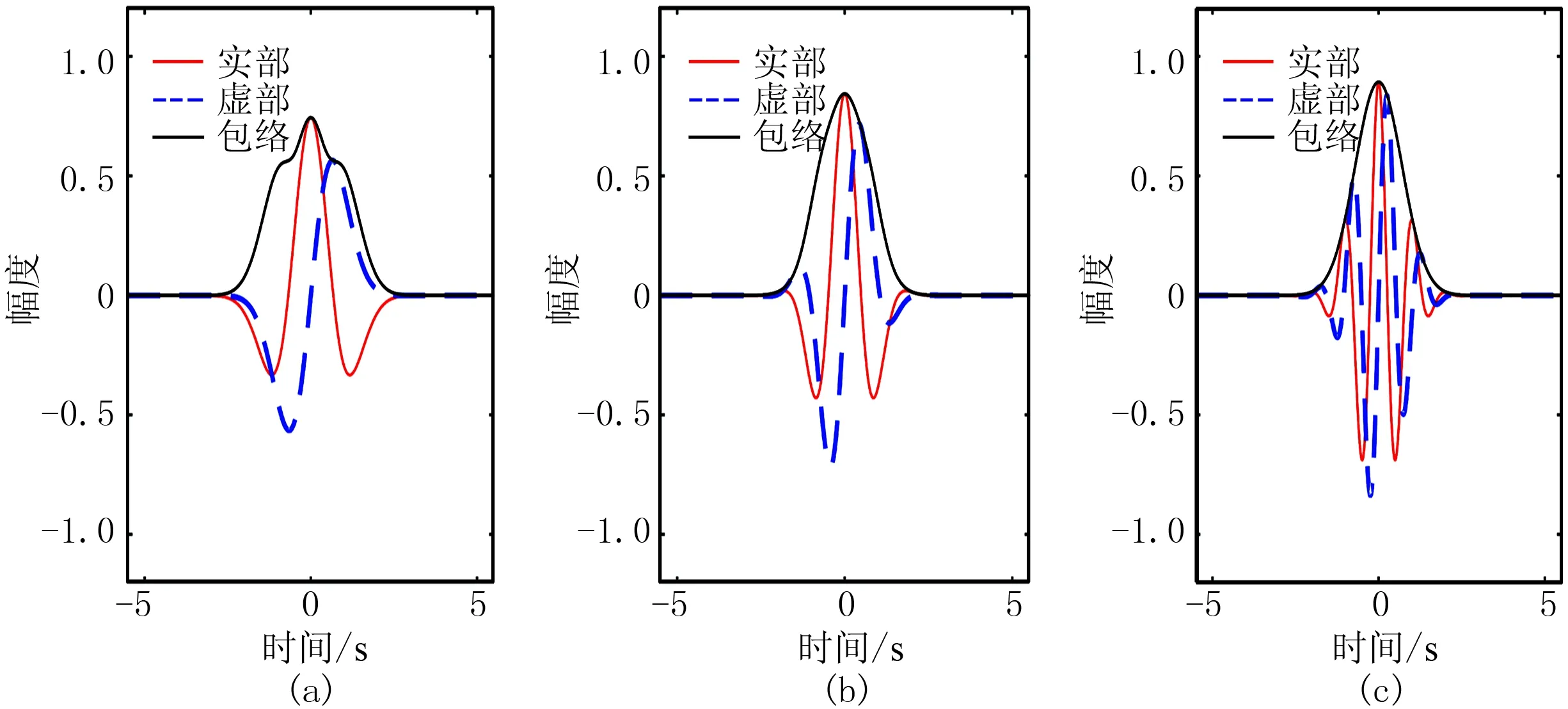
图3 不同σ的三参数小波(a)Γ=(1,1,0)；(b)Γ=(3,1,0)； (c)Γ=(6,1,0)

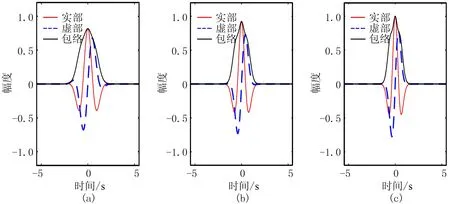
图4 不同τ的三参数小波(a)Γ=(2.5,1,0)；(b)Γ=(2.5,2,0)； (c)Γ=(2.5,3,0)

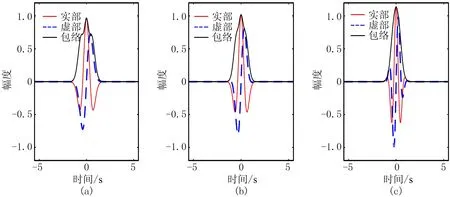
图5 τ较大时不同σ的三参数小波(a)Γ=(1,3,0)；(b)Γ=(3,3,0)； (c)Γ=(6,3,0)

图6 不同β的三参数小波(a)Γ=(π,3,0)； (b)Γ=(π,3,0.6)； (c)Γ=(π,3,1)； (d)Γ=(π,3,2)

最后讨论β对小波的影响，β作为能量延迟因子对小波形态的影响较复杂。如果改变β，会使衰减函数产生时间延迟，即窗口在时间轴滑动。当β取三角函数周期的整数倍时，窗口就按周期的整数倍移动，则小波只会发生时移；当β为周期的非整数倍时，窗口内被改造的函数成分发生变化，因此小波不仅发生时移，还产生变形。由不同β的三参数小波(图6)可见：①固定σ为π(周期为2)，当β=0.6时，小波不仅发生时移，还产生变形(图6b)，这种变形即为相位延迟。可以理解为由于β改变，导致窗口平移(也可以认为窗口不变，三角函数平移β个单位)，则相位延迟σβ个单位。②当β=1.0(为周期的一半)时，小波实部与虚部都发生反转，且产生1s的时移(图6c)。③当β=2.0(图6d)时，小波只产生2s的时移，波形并没有发生改变。由此可见：三参数小波在β为周期的整数倍时，可以匹配零相位子波；在β为周期的非整数倍时，可以匹配非零相位子波。

4 模型测试及实际地震资料应用

4.1 模型测试

通过模型测试三参数小波和Morlet小波时频分析的差异，测试模型是反射系数变化的薄互层地质模型(图7a)。图7为测试模型及不同小波的时频谱。由图可见： ①对比ω0=5rad/s的Morlet小波(图7c)和Γ=(5,2,0)的三参数小波时频谱(图7d)发现，前者只有一个强能量团，看不到任何薄层信息，后者显示高频能量呈锯齿状分布，即利用三参数小波做基小波可反映部分薄层信息，而Morlet小波不能精确地反映地下的地质细节。②对比ω0=1rad/s的Morlet小波(图7e)和Γ=(1,2,0)的三参数小波时频谱(图7f)发现，当ω0较小时提高了Morlet小波的时间分辨率，但这是以牺牲频率分辨率为代价的，其频率分辨率几乎为零(图7e)，也就失去了时频域联合解释的意义； 在三参数小波时频谱(图7f)中，主频带仍然在50Hz附近，且能量团发生分裂，出现多个锥形谱，可识别薄互层地质结构，即三参数小波的灵活性高，能更好地刻画复杂地质现象。③对比Γ=(5,2,0)(图7d)和Γ=(1,2,0)的三参数小波时频谱(图7f)发现，后者(即当σ取较小值时)的时间分辨率更高，刻画薄层的能力更强。

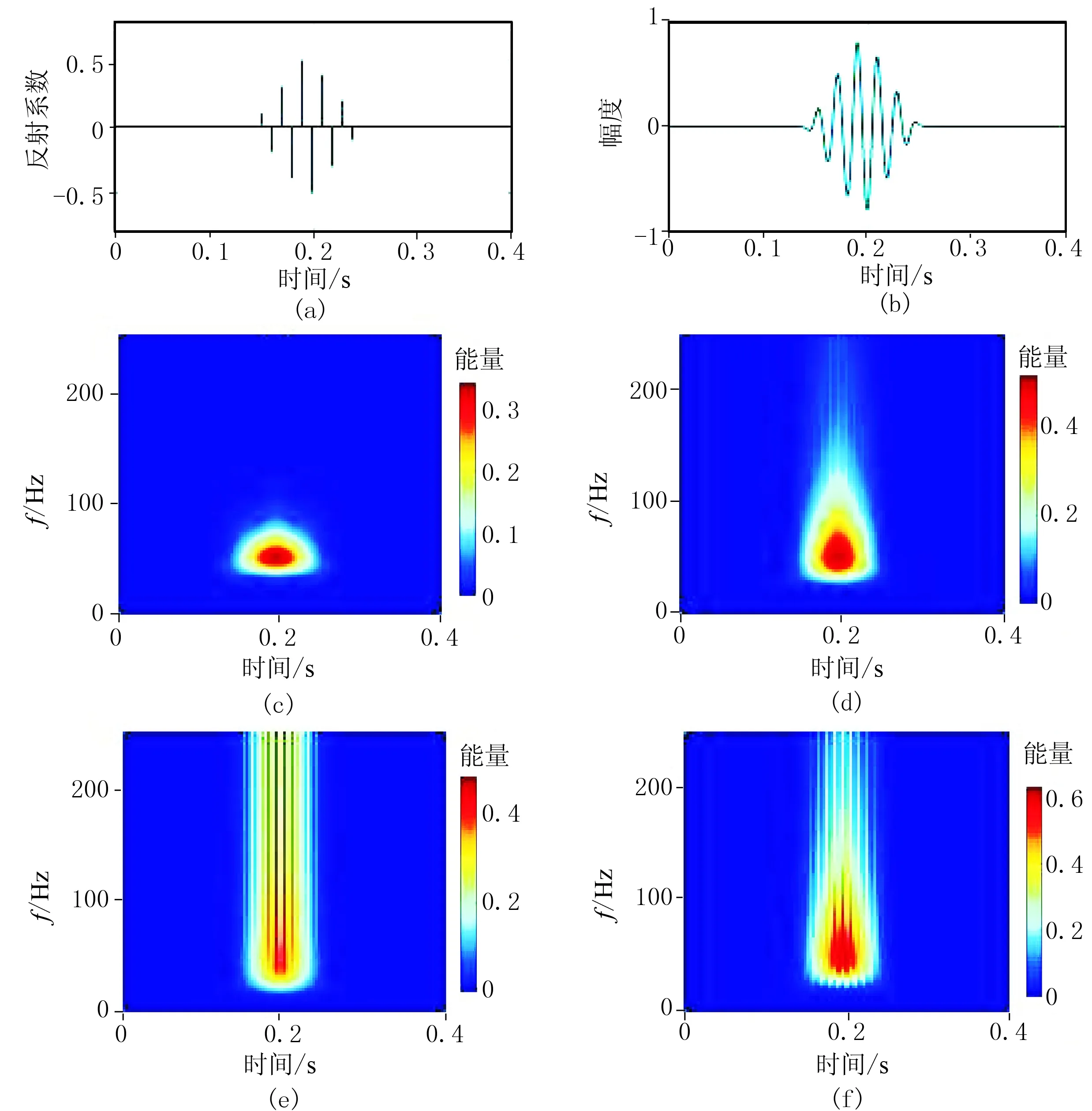
图7 测试模型及不同小波的时频谱(a)反射系数序列； (b)图a数据与50Hz雷克子波褶积得到的地震记录； (c)ω0=5rad/s的Morlet小波时频谱；(d)Γ=(5,2,0)的三参数小波时频谱； (e)ω0=1rad/s的Morlet小波时频谱； (f)Γ=(1,2,0)的三参数小波时频谱图a中的反射系数正、负相间，其绝对值从0.1增大到0.5，再从0.5减小至0.1，共计10个反射系数，相邻两个反射系数的时间间隔为10ms

4.2 实际地震资料应用

4.2.1 三参数小波频谱分解

实际资料来源于渤海某靶区，目的层砂体薄厚不均，叠置关系复杂，砂体横向分布不稳定，砂、泥岩交替频繁。靶区内河道众多，多期河道纵、横分布，横向变化快。对于河流相储层而言，刻画河道的展布及边界，弄清河道之间的叠置关系是储层预测中非常重要的工作。

三参数小波频谱分解的关键在于参数的选取，结合前文的研究以及实际地震资料，参数选取时需要注意以下问题： 第一，σ取较小值更利于刻画地质细节。第二，当τ值较大(≥3)时，由于σ对小波形态的影响变小，所以不同σ的频谱分解结果差异不大(图5)。如由三参数小波频谱分解切片(图8)可见， 即使σ存在很大差异，处理结果也没有太大区别。第三，前文研究表明，令β=0可匹配零相位地震子波，β≠0虽然可以更好地匹配非零相位子波，但由于β非零造成基小波时移，则频谱分解后的数据体也会产生时移，导致对地质体埋深的错误解释。

图9为不同β的三参数小波频谱分解切片。由图可见：当β=0时，在目的层下方38ms的切片(图9a)上可见河道信息；当β=5时，在目的层下方38ms的切片(图9b)上见不到任何河道信息，而在目的层下方92ms的切片(图9c)上可见河道信息。可见，β非零会造成对河道埋深的错误解释。

图8 三参数小波频谱分解切片(40Hz)(a)Γ=(1,3,0)； (b)Γ=(6,3,0)

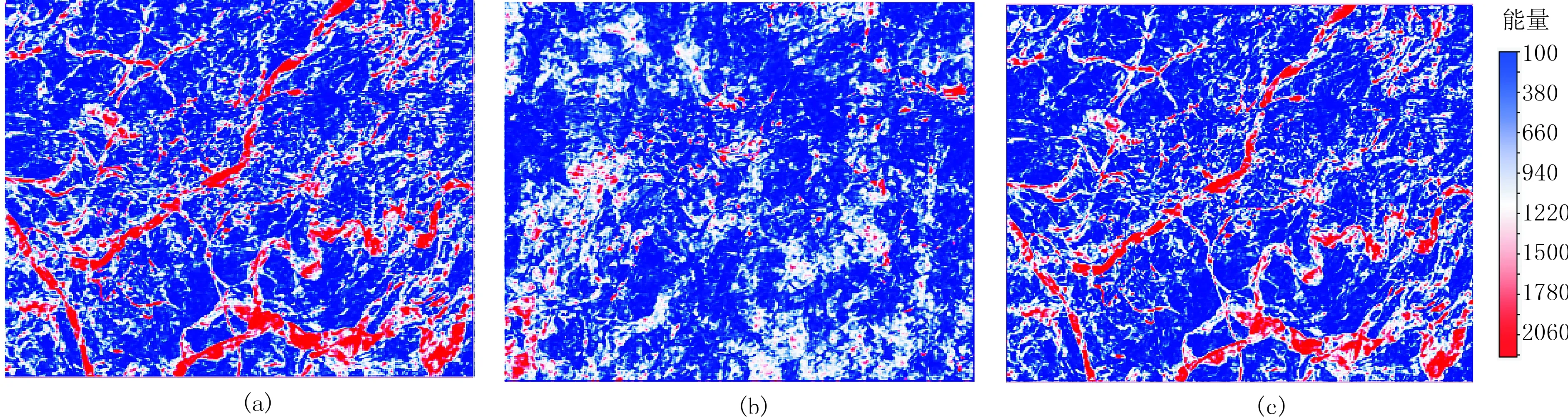
图9 不同β的三参数小波频谱分解切片(40Hz)(a)Γ=(2.5,0.5,0)(目的层之下38ms)； (b)Γ=(2.5,0.5,5)(目的层之下38ms)； (c)Γ=(2.5,0.5,5)(目的层之下92ms)

针对该区目的层段的实际情况提取地震子波，并与不同的三参数小波做相关，优选相关性大的参数组合作为该目的层段的小波[7]。本文选择Γ=(1,0.5,0)进行频谱分解，并与Morlet小波的频谱分解效果进行对比。对于河流相储层而言，主要从河道展布及边界刻画是否清晰作为评价标准。图10为三参数小波和Morlet小波的频谱分解结果。由图可见：在20Hz切片上，Morlet小波的信噪比低，对河道边界(红色圆圈内)的刻画不如三参数小波清晰；在80Hz切片上，在Morlet小波展示的河道(蓝色圆圈内)展布不连续，边界不清晰，而三参数小波的频谱分解效果较好。综上所述，在该区的河流相储层预测中，三参数小波频谱分解的效果优于Morlet小波。

4.2.2 RGB混色融合

利用频谱分解预测储层时，可采用分频解释技术获得离散的单频体，但由于某个地质体在时频域的响应不仅仅对应一种频率，所以每个单频体只反映地质体的一个时间厚度信息，为了提高解释精度，需要综合这些单频信息，RGB混色融合技术的基本思想即源于此[22]。这里的R代表红色，G代表绿色，B代表蓝色，将三种颜色按照不同比例叠加，可以产生不同的颜色。本文用20Hz数据体作为红色分量，40Hz数据体作为绿色分量，80Hz数据体作为蓝色分量，即R、G、B分别代表低、中、高频。图11为20、40和80Hz切片的RGB融合显示。由图可见，通过RGB融合显示，河道的能量更强，边界更清晰，展布更连续。

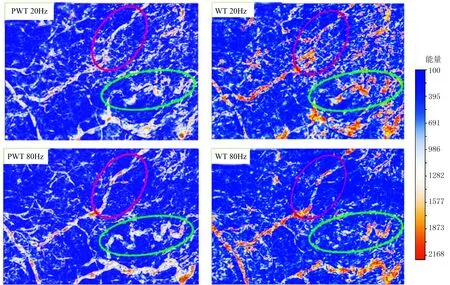
图10 三参数小波(PWT)和Morlet小波(WT)的频谱分解结果

图11 20Hz、40Hz和80Hz切片的RGB融合显示

5 结论

(1)三参数小波的灵活性高，σ影响小波的震荡程度。τ影响小波的宽窄，当τ较大时，σ对小波的影响减弱。β的影响颇为复杂，当其为周期的整数倍时，小波只产生时移，可以匹配零相位子波；当其为周期的非整数倍时，小波不仅产生时移，而且产生相位延迟，可以匹配非零相位子波。同时需要注意，β非零造成河道埋深解释错误。

(2)三参数小波变换较Morlet小波变换具有较好的时频分辨率，能更好地刻画薄互层内细微的地质沉积结构。三参数小波变换处理结果的信噪比高，展示的河道边界清晰、砂体展布连续。因此基于三参数小波的频谱分解方法可以高精度地预测储层。

(3)实际处理中可将从目的层段提取的地震子波与三参数小波做相关，优选相关性大的参数组合，从而获得最佳的三参数小波。