二维黏滞声波方程的优化组合型紧致有限差分数值模拟

汪 勇 徐佑德 高 刚 桂志先 陈 英 王亚楠

(①油气资源与勘探技术教育部重点实验室(长江大学)，湖北武汉 430100； ②长江大学地球物理与石油资源学院，湖北武汉 430100； ③中国石化胜利油田分公司勘探开发研究院西部分院，山东东营 257001；④东方地球物理公司装备处测量中心，河北涿州 072751； ⑤东方地球物理公司研究院地质研究中心，河北涿州 072751)

1 引言

目前，常用的地震波场数值模拟方法主要有射线追踪法和波动方程法，其中波动方程法有伪谱法、有限元法、边界元法、谱元法和有限差分法[1-5]。随着数值模拟技术的发展和生产实践的要求，围绕着提高有限差分计算效率[6]、模拟精度[7]、算法稳定性[8-9]、处理复杂介质[10-11]、吸收边界条件[12]和压制数值频散[13-15]等方面，已经提出了许多方法,取得了大量有意义的研究成果。

提高差分格式数值计算精度最直接的方法就是在差分计算时增加网格节点数，但会大大增加计算量和存储空间。紧致差分方法恰好能够较好地解决这个矛盾，同时紧致差分是一种隐式差分格式，具有较好的稳定性，这些优势也使之成为目前研究较多的有限差分方法之一。Dennis等[16]针对Navier-Stokes方程提出了空间四阶的紧致差分格式，能够使用粗网格获得较高的精度；Lele[17]构造了求解一阶导数和二阶导数的紧致差分格式；Adams等[18]提出了紧致非震荡(Essentially Non-oscillation，ENO)差分格式，用于求解激波湍流相互作用问题；Chu等[19]提出了三点组合型紧致差分格式，并将其用于求解对流扩散方程。也有不少学者将紧致差分格式用于声波、弹性波和复杂介质等地震波场数值模拟，取得了许多研究成果[20-24]。

地层的黏弹性对地震波产生的吸收和衰减规律非常复杂，所以研究地震波在黏弹性介质中的传播规律对地震勘探有着重要的意义。李晓波等[25]模拟了地震波在斑状饱和介质中的传播，分析了斑状饱和介质中孔隙度及含气饱和度的变化对地震波传播特征的影响；姚振岸等[26]进行了黏弹各向异性介质中的微地震波场模拟，并分析了微地震信号的传播特性和偏振特性；汪勇等[27]利用近似解析离散化算子计算空间导数，对黏滞声波方程进行了数值模拟；马灵伟等[28]、罗文山等[29]、姚振岸等[30]基于不同方法对不同的黏弹介质模型进行了数值模拟。

组合型紧致差分格式在黏滞声波方程地震波场模拟中的应用，尚未见到文献报道。本文在黏滞声波方程时间二阶离散格式的基础上，将组合型紧致格式应用于位移场空间导数的求取，实现了二维黏滞声波方程地震波场的数值模拟。

2 组合型紧致有限差分方法原理

早期的紧致差分格式是基于Hermite多项式构造而来。Lele[17]对Hermite公式进行了扩展，构造了求解一阶导数和二阶导数的紧致差分格式(Compact Finite Difference，CD)，其特点是用相邻节点的函数值和导数值计算待求节点上的导数值。而常规中心差分(Central Finite Difference，FD)仅利用函数值求解中心节点的导数值。一般情况下，在相同网格间距时，CD格式比常规FD格式具有更高的精度和更小的数值频散[20]。

Chu[19]等构造了精度更高的三点六阶组合型紧致差分(Combined Compact Difference，CCD)格式

(1)

式中：f为一维函数；h为空间采样间隔。上式CCD格式只需要相邻的三个节点就可以同时求得一阶和二阶导数的六阶精度近似值，比常规CD格式的节点数更少。并且式(1)中的一阶导数和二阶导数是耦合的，既可以同时求出，又利于波形保真。

3 黏滞声波方程组合型紧致有限差分法分析

经常使用Kelvin-Voigt体模型描述声波在非完全弹性介质中的传播，认为地震波吸收系数与地震信号频率的平方成正比，这与实际情况较为吻合。该模型假定介质的应力包括两部分，一部分是弹性应力，另一部分是黏滞应力，其中弹性应力与应变成正比，黏滞应力与应变的时间变化率成正比。该模型的二维黏滞声波方程可以表示为

(2)

利用时间二阶导数的二阶精度近似式

(3)

代入式(2)，可以得到位移场三层显式差分格式

(4)

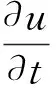
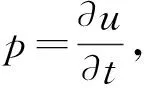
(5)

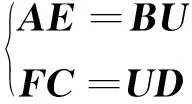
(6)

式中：A和C为式(1)左端的差分系数矩阵，阶数分别为2M×2M和2N×2N；E和F为待求位移场空间一阶和二阶导数矩阵，阶数分别为2M×N和M×2N；B和D为式(1)右端的差分系数矩阵，阶数分别为2M×M和N×2N；U为位移场矩阵，阶数为M×N。这些矩阵分别为

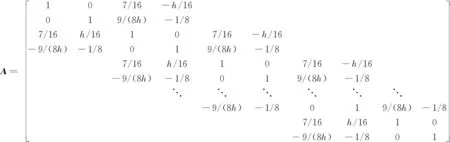
(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

3.1 精度分析

不论是利用CCD格式，还是利用常规的七点六阶FD格式或五点六阶CD格式[17]，进行黏滞声波方程数值模拟时，它们在时间层推进方式上是相同的，即都是利用差分格式式(5)，时间差分为二阶精度。CD、FD和CCD不同之处在于它们分别利用不同的差分格式计算位移的空间导数。这三种格式计算的二阶导数的截断误差主项系数分别为-17/(8!)、72/(8!)、-2/(8!)。虽然三种方法都能达到空间6阶精度，但截断误差有较大的差别，FD和CD格式计算二阶偏导数的截断误差约是CCD的36倍和8.5倍，说明CCD方法具有更小的截断误差和更高的差分精度。

应用一维黏弹介质模型比较CCD、CD和FD三种格式的数值模拟精度，其中模型长度为6000m、声波速度为4000m/s、品质因子Q=10。数值模拟中，Δt=1ms，h=40m。在模型的3000m处加载频率为10Hz简谐波震源，可得700ms时刻的模拟波形(图1)。式(2)的一维黏滞声波方程的解析解见文献[27]。从局部放大图中可以看出，CCD格式的数值模拟结果与精确解析解最接近，其模拟精度最高，CD和FD格式次之，这是由于在计算空间导数时截断误差不同。

3.2 频散分析

频散分析既是判断数值模拟方法优劣的重要指标，也是确定空间网格大小的重要依据。通过对黏滞声波方程的组合型紧致差分格式进行数值频散分析，进一步分析方法的适用条件。

首先考虑x方向，令

(15)

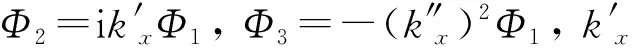
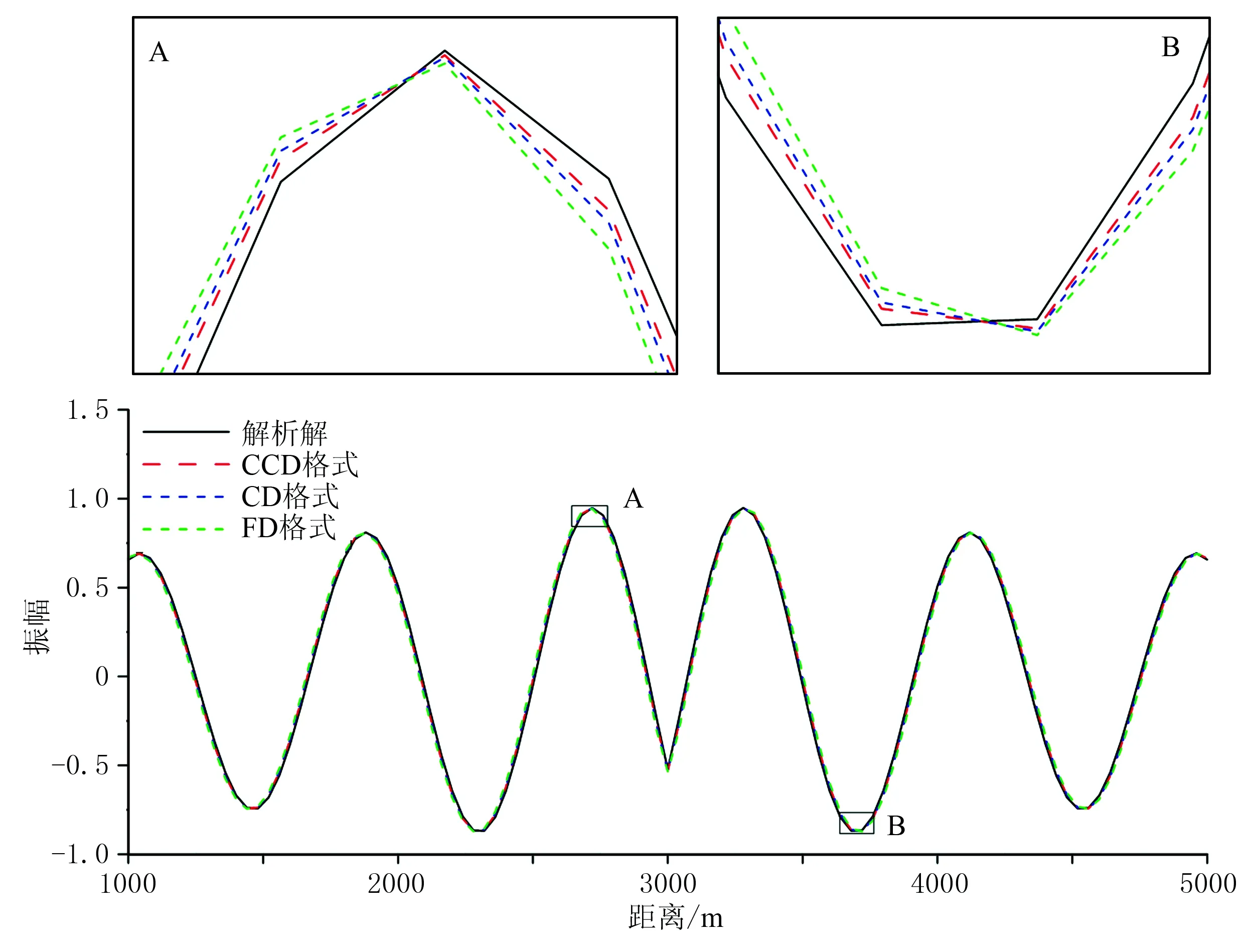
图1 三种差分格式的一维黏滞声波方程数值模拟波形(700ms)(下)及其局部放大显示(上)

代入差分格式式(1)，解方程组可得

(16)

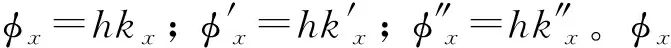
同理可得z方向的解

(17)

将式(16)和式(17)代入黏滞声波方程的差分格式(5)中，并令c0=vΔt/h为库朗数，χ=kv′Δt(其中v′为数值波速，v是真波速)，利用欧拉公式，化简可得CCD格式频散关系

(18)

上式表明，黏滞声波方程的频散关系不仅与空间间距的取值有关，而且与介质的品质因子有关。通过上述频散关系，确定φ后可以解得对应的χ，且定义数值波速与真实速度的比值为

(19)

在理想情况下，如果不存在数值频散则速度比γ恒等于1。γ偏离1越大，则说明该方法的数值频散越严重，反之则说明该方法能更好地压制数值频散。取θ=π/4，计算CCD格式的速度比与φ的关系曲线，如图2所示。

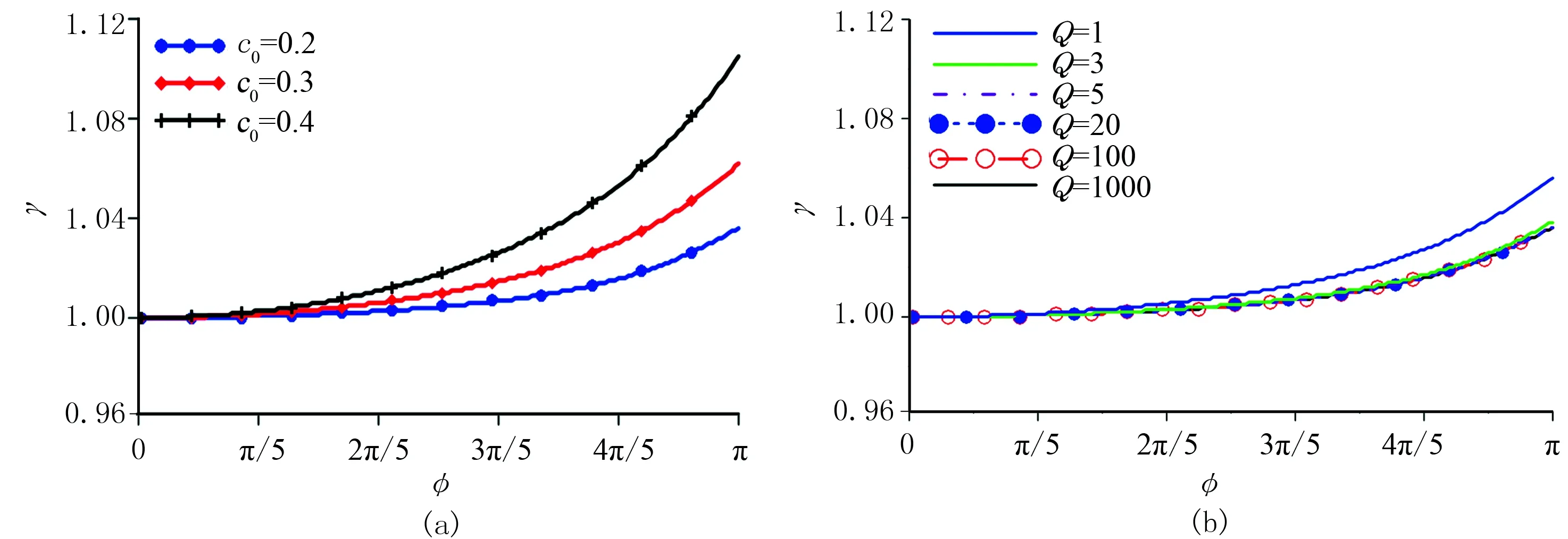
图2 黏滞声波方程CCD格式速度比曲线(a)Q=100，c0不同; (b)Q不同，c0 =0.2

取φ∈[0,π]作为横坐标，它是波数与空间间距的乘积，单位波长内采样点数N=2πφ，所以横坐标也可以看作N由∞逐渐减小至2。从图中的速度比曲线可以看出：①随着空间采样点数的减少，速度比曲线逐渐偏离1，频散现象逐步加剧。CCD方法的空间网格长度过大时，速度比曲线上翘，数值速度大于真速度。②当库朗数增加时，频散加剧，说明即使空间网格间距选取合适时，加大时间采样间距也会增加数值频散。③品质因子对速度比曲线影响不大，当Q>5时，速度比曲线基本重合，具有相同的频散特征。但这不能说明品质因子大小与数值频散无关，因为品质因子影响着频率衰减的快慢，进而影响了传播过程中地震子波的波长，在同样网格间距情况下，每个波长内的采样点也在随之改变，后文用波场快照做进一步分析。④在不考虑Q值大小的情况下，当c0分别为0.2、0.3和0.4时，为保证无数值频散，每个波长内需要6.7、10.0和13.3个样点。

利用二维均匀模型验证以上分析的结论。设置模型长度和深度均为4000m，声波速度为4000m/s，震源子波为sin(2πf0t)exp(-π2f0t2/4)，其主频为40Hz，Δt=0.75ms。图3为CCD和常规FD格式不同品质因子和网格间距时的波场快照，可以看出：①图3a中品质因子为2000，近似完全弹性介质，传播过程中近似无衰减。根据频散分析结论，每个波长需采样6.7个点，取网格间距为15m，340ms波场快照无明显数值频散。②当网格间距为20m时，采样略微不足，图3b在对角线方向上频散不明显，而在x、z轴方向出现数值频散，数值波速大于真实速度。③图3c中的品质因子仅为20，波场清楚，无数值频散。这是由于地震波在黏弹介质中传播时，随传播距离的增加频率降低衰减、波长增加，有利于压制数值频散。④由于地震子波频率衰减，波长增加，图3f所示结果平滑，无明显数值频散，而图3d和图3e均存在较严重的数值频散，说明CCD格式比常规五点六阶FD格式具有低数值频散的优势，能够适用于粗网格和大尺度模型的地震波场数值模拟。

图3 均匀模型CCD和常规FD格式不同品质因子和网格间距时的340ms时刻波场快照(a)CCD，Q=2000，Δx=15m; (b)CCD，Q=2000，Δx=20m; (c)CCD，Q=20，Δx=20m;(d)FD，Q=2000，Δx=15m; (e)FD，Q=2000，Δx=20m; (f)FD，Q=20，Δx=20m

3.3 稳定性分析

稳定性条件是有限差分数值模拟中一个非常重要的问题，是影响差分方法计算效率的重要因素。采用与文献[31]相同的Fourier方法对黏滞声波方程的组合型紧致差分格式进行稳定性分析，可得稳定性条件为

(20)

式中Ψ=19.2。可以看出，时间步长Δt的取值不仅与网格间距h和波速v有关，而且与介质品质因子Q和谐波频率ω有关。当Q趋向无穷大时，黏弹介质可以看作完全弹性介质，则时间二阶、空间六阶精度的CCD格式的稳定性条件变为c0=vmaxΔt/h<0.456，其中vmax为最大波速。

对式(20)进行数值分析，依然定义c0=vΔt/h，并计算它随速度、品质因子、频率的变化曲线，结果如图4所示，可以看出：①当品质因子和频率一定时，满足稳定性要求的库朗数随速度的增加而减小，即稳定性变差，要求的时间步长越小。②当地层速度一定，品质因子小于100时，库朗数随品质因子的减小而急剧变小。当品质因子增加时，库朗数随之增加，稳定性变好，满足要求的时间步长越大。③当品质因子达到2000时，介质可以近似为完全弹性介质，库朗数趋近于常数0.456，不随速度的变化而改变。④稳定性还和地震子波主频有关，当速度和品质因子不变时，稳定性随频率的降低而变差。由于黏弹介质中地震波主频会降低，降低的快慢与介质的品质因子有关，所以要求的稳定性会随传播时间的增加而改变，即要求的时间步长应该越来越小。若仅按照激发地震主频得到的时间步长进行模拟，在传播一定距离后，差分格式可能就不稳定了，这与完全弹性介质波动方程数值模拟不同，因为完全弹性介质中的地震波只会产生振幅衰减，而主频不会降低。

图4 差分格式式(5)的库朗数与品质因子、速度和频率的关系曲线(a)速度—库朗数曲线; (b)品质因子—库朗数曲线; (c)频率—库朗数曲线

3.4 差分格式优化

为了进一步提高组合型紧致差分格式的紧致性，在差分格式式(1)的基础上建立四点组合型紧致差分格式

(21)

为了满足2～6阶精度泰勒公式截断误差的要求，上式中的差分系数ai,bi和ci必须满足

(22)

为确定上述方程中的未知差分系数ai、bi和ci，按照Tam等[32]提出的频散关系保持的思路，求取在最小数值频散条件下的差分系数[33，34]。

与3.2相同，可以得到式(21)的频散关系

(23)

式中：φ′=k′h；φ″=k″h。k、k′和k″分别表示真波数、一阶和二阶导数的数值波数(或称修正波数)。

优化的目标是在某个选定的波数范围内，确定式(21)中的8个未知差分系数，使得修正波数尽可能地接近真波数，所以定义误差函数为

(24)

式中：R(φ′)表示φ′的实部；W(φ)为一个加权函数，目标是使误差函数解析可积，它是φ-R(φ′)的分母部分。选定c2和c3为变量，则确定Er的最小值为条件极值问题。采用拉格朗日乘数法进行求解，可得

(25)

由式(22)和式(25)表示的8个方程，可以确定8个优化后的差分系数为：a1=0.8873686;a3=0.0491178；b1=0.149532；b2=-0.2507682；b3=-0.0123598；c1=0.0163964；c2=-1.9692791；c3=1.9528828。将差分系数代入式(19)，得到优化后的组合型紧致差分格式，简称OCCD。优化前、后频散关系曲线，如图5所示。

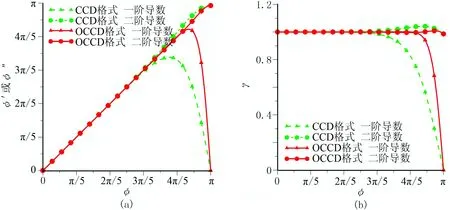
图5 CCD和OCCD格式频散曲线(a)波数—修正波数曲线; (b)速度比曲线

从图5可以看出，差分系数优化后，不论是一阶导数还是二阶导数的修正波数都更接近真波数，速度比也更接近理想值1。优化前，满足一阶和二阶导数速度比等于1(或修正波数等于真波数)的最小φ为0.1833，而优化后满足同样条件的最小φ为0.2556，说明优化后的OCCD格式提高了组合型紧致差分格式的紧致性，能更好地压制数值频散，从而能使用更粗的网格，进一步提高了计算效率。

4 PML边界条件

本文采用完全匹配层(Perfectly matched layer，PML)吸收边界。按照王守东[35]和刘有山等[36]推导声波PML控制方程的思路和方法，略去推导过程，直接给出二阶黏滞声波方程的PML边界条件的控制方程

(26)

式中：u1、u2、A1和A2是引入的中间变量；d(x)和d(z)分别是x和z方向的衰减系数，分别衰减这两个方向传播的波。衰减函数采用高刚等[37]提出的余弦型吸收衰减函数，衰减幅度因子为500，吸收边界厚度为20个网格间距。

5 模型试算

利用均匀介质模型和Marmousi模型说明OCCD差分格式的黏滞声波方程数值模拟效果。

5.1 均匀介质模型

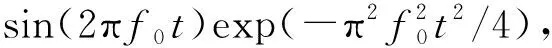
图6为Q=20、50、200和完全弹性(Q=+∞)四种情况时模拟的220ms时刻波场快照，波场非常清晰，没有数值频散现象。

提取以上四个波场快照中的波形记录(z=1250m)，如图7所示。从中可以看出，波形曲线平滑，无数值频散，且随着品质因子的减小，地震波振幅发生显著衰减，频率降低，波形展宽，波长增加。

为了说明本文差分方法在PML条件下对边界反射的吸收效果，将图6b的传播时间延长至410ms，图8a和图8b分别为未使用和使用PML边界条件时的波场快照，图8c为二者之差，是只含边界反射的波场快照。可以看出，本文差分格式在PML控制方程作用下，边界反射得到了较好的吸收，有效波没有明显改变，边界处理效果可靠。

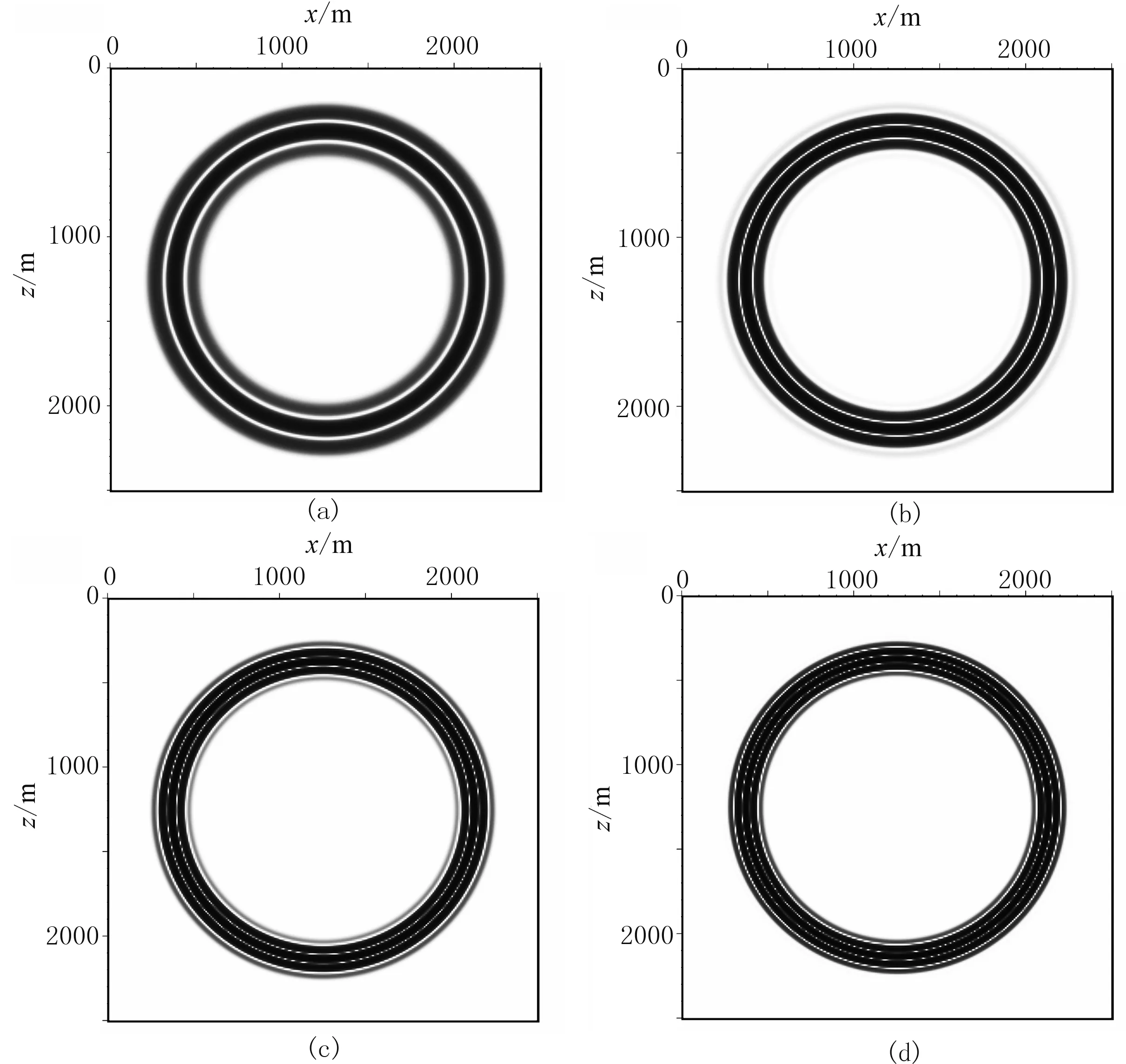
图6 均匀模型OCCD差分格式在Q=20(a)、50(b)、200(c)和+∞(d)时模拟的220ms时刻波场快照

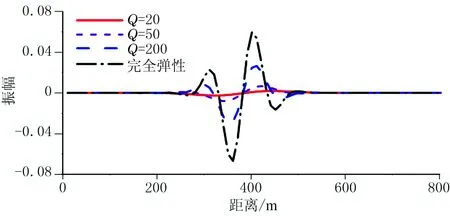
图7 均匀模型不同品质因子时的波形曲线

5.2 Marmousi模型

用经典的二维Marmousi纵波速度模型进行数值模拟。速度范围为1729～5500m/s，品质因子根据经验公式Q=14v2.2计算，范围为46.7～595.6(图9)。模型网格数为501×501，网格间距为5m，时间步长为0.2ms，纵波震源位于(1250m，0)，激发40Hz的Ricker子波，采样时间2s。

图10为对Marmousi模型分别进行黏滞声波方程和声波方程数值模拟得到的波场快照，可见波场快照平滑清晰，无数值频散，且边界吸收效果较好，无明显边界反射，这说明本文算法对复杂模型的适用性。图11是两种方程分别模拟得到的地面地震记录。

图8 未使用(a)和使用(b)PML边界条件时的410ms时刻波场快照及二者之差(c)

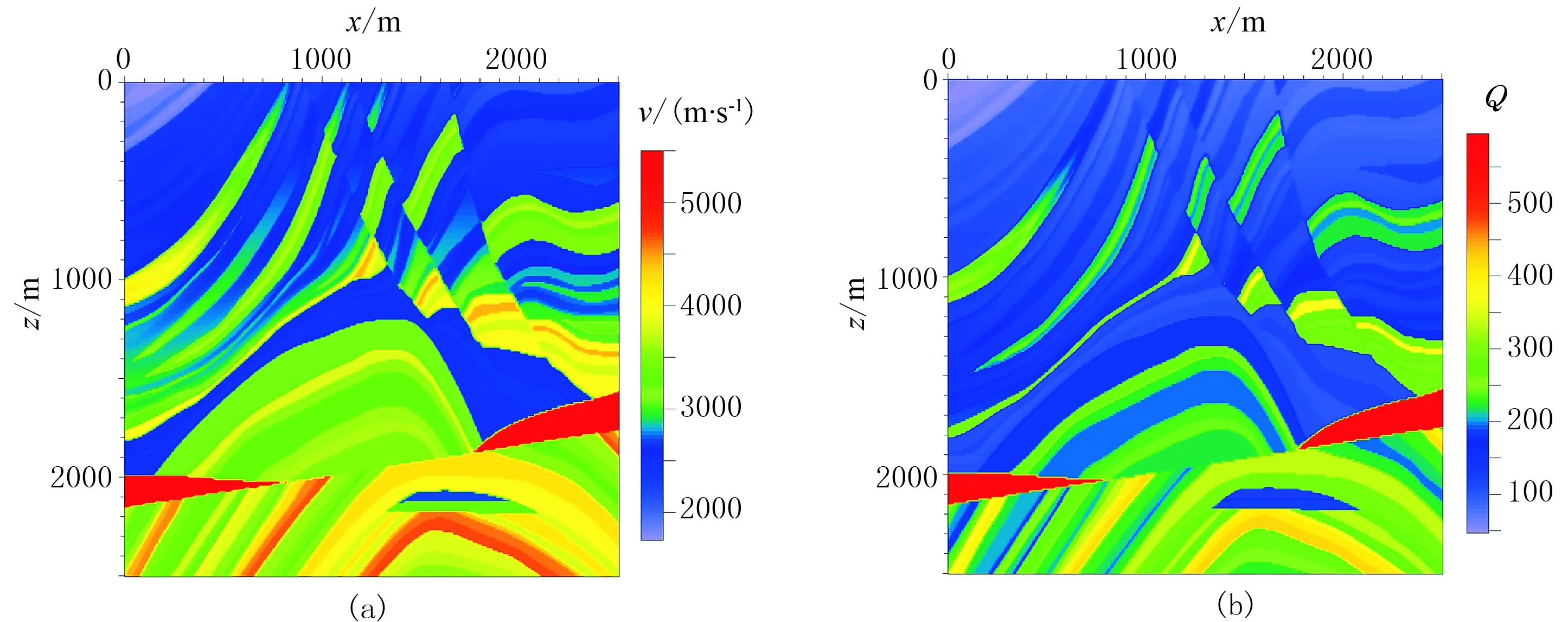
图9 Marmousi模型(a)速度; (b)品质因子

图10 Marmousi模型黏滞声波方程(上)和声波方程(下)模拟的波场快照(a)260ms; (b)460ms; (c)660ms; (d)860ms

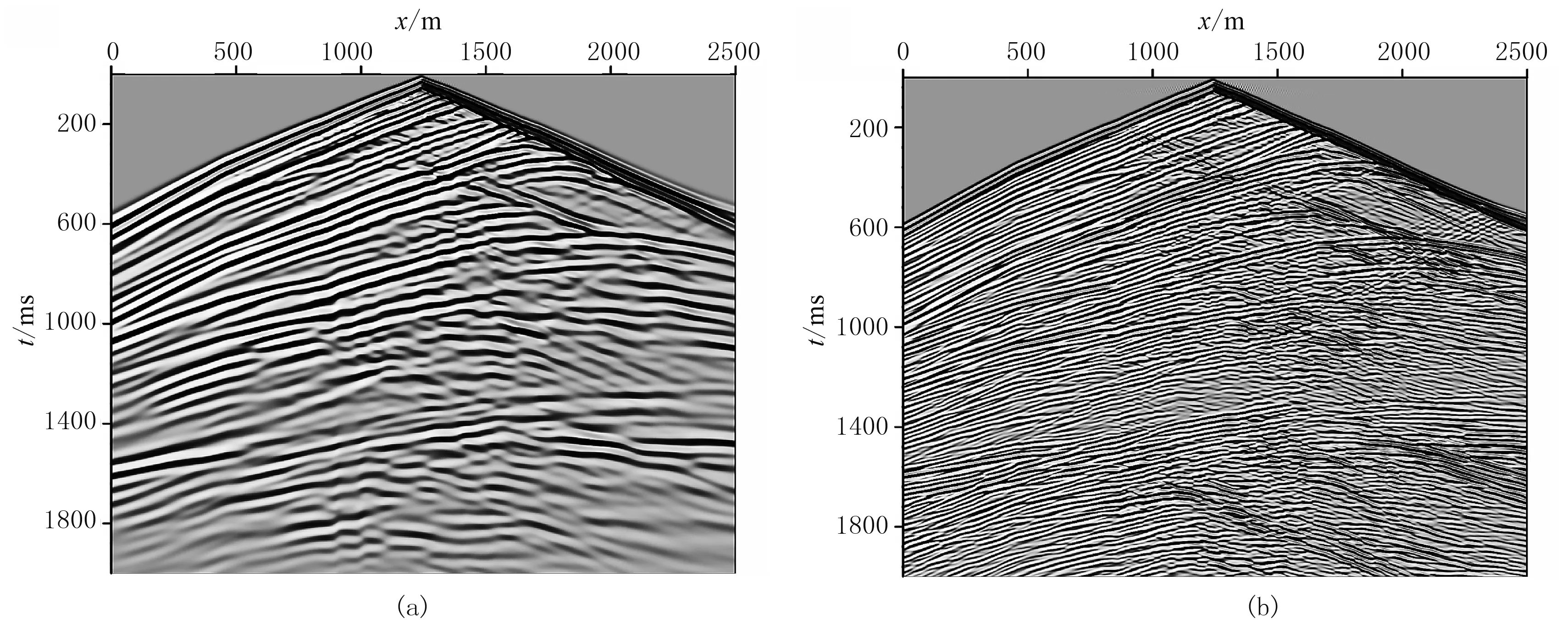
图11 Marmousi模型黏滞声波方程(a)和声波方程(b)模拟的地震记录

由于波前扩散造成振幅衰减，深部反射振幅明显减弱，为了显示清晰，对地震记录进行了瞬时自动增益控制(AGC)处理，时窗长度为500ms。对比二者可以看出，采用黏滞声波方程数值模拟时，除了波前扩散造成的振幅衰减以外，地震波还受到了黏弹介质的吸收衰减作用，使得反射波振幅衰减幅度大于声波方程模拟的结果，且地震波的频率也会随传播的距离的增加而减小。

图12是从模拟得到的地面地震记录中提取并增益处理后的单道记录波形图(x=600m)。从图中可以看出，在同样的AGC处理时，黏滞声波记录的振幅小于声波记录。此外，黏滞声波记录的子波延续时间大于声波记录，同时反射波的个数也少于声波记录，并且随传播时间的增加，差异更加明显，这也导致了黏滞声波方程模拟结果的垂向分辨率小于声波。

为了分析两种模拟记录频谱上的差别，利用广义S变换，对图12单道地震记录进行时频分析，结果如图13所示。由时频分析结果可见，声波模拟记录(图13b)的振幅会随时间的增加而减小，这是波前扩散造成的。在振幅衰减的同时，反射波的主频基本不变，与激发主频一致，约为40Hz。而黏滞声波记录(图13a)除了振幅衰减以外，其主频会降低，在300ms时，主频为30Hz。在1100ms时，主频变为20Hz左右，在1600ms～1800ms时，主频进一步降至15Hz左右。对比两种记录的时频谱，在1400ms～1900ms时，声波模拟结果中有4个明显区分的振幅谱能量峰值区，对应时间域的4个主要反射波，而黏滞记录只有一个很难区分的峰值区，这也从频率域说明了地震垂向分辨率的降低。

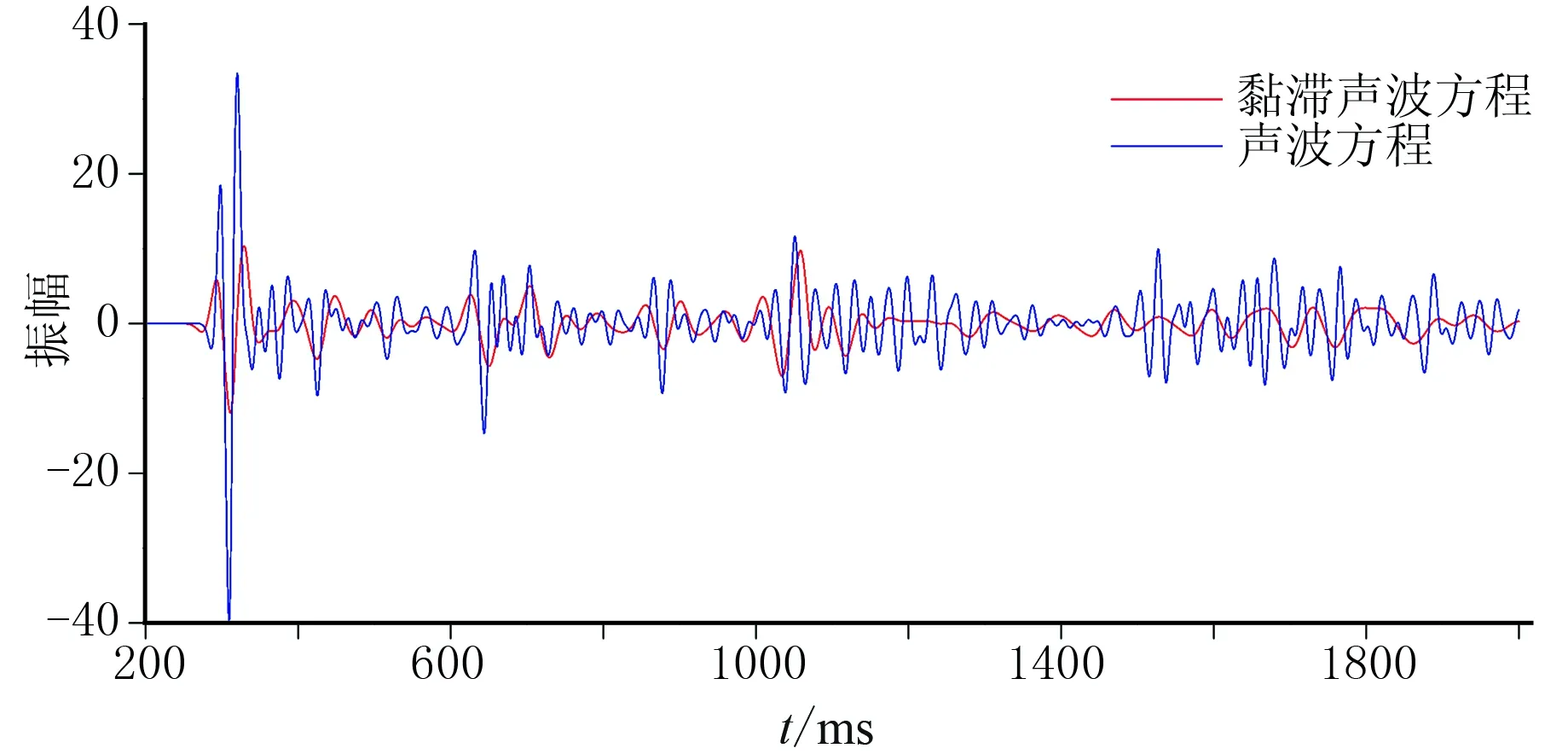
图12 x=600m处的单道地震记录对比

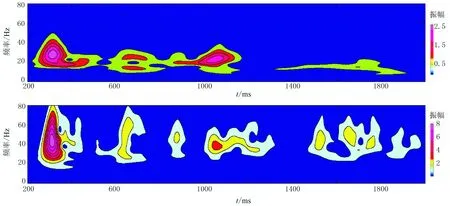
图13 Marmousi模型黏滞声波方程(上)和声波方程(下)模拟的x=600m处单道地震记录时频谱

6 结论与建议

本文从组合型紧致差分格式出发，建立了时间二阶、空间六阶的黏滞声波方程的差分格式，对该差分格式进行了模拟精度、频散关系、稳定性和格式优化分析。最后在黏滞声波PML控制方程的基础上，利用优化组合型紧致差分格式，对均匀介质和Marmousi模型进行了数值模拟。数值模拟结果显示地震波场特征清晰，边界反射吸收效果较好，验证了该方法的适用性，也说明该方法还可以进一步推广到二维或三维的各向异性介质和双相介质等复杂介质的声波或弹性波数值模拟中。

文中建立的黏弹介质声波方程为时间二阶精度，在今后的研究中，应考虑提高时间差分精度，以提高数值模拟的计算精度。此外，可以通过其他有限差分系数优化的方法[38，39]优化该差分格式，提高计算精度和效率。