“庖丁解牛” 意在素养
——“牛顿法:用导数方法求方程的近似解”教学设计
2018-11-30
●
(浙江师范大学附属中学,浙江 金华 321004)
在人教版普通高中课程标准实验教科书中,介绍了两种求高次方程近似解的方法:二分法和牛顿法.“二分法”之后为何补充“牛顿法”?是进一步强调“近似计算”,抑或“牛顿法”有其不可替代的独特作用?
1 教育价值
通过剖析牛顿法的思维方式及其操作过程,进一步考察其数学本质,可发现牛顿法确实具有重要的教育价值.
1)“近似解”与“精确解”相得益彰,可有效端正学生的数学观.数学的确定性可培养学生的理性和严谨性,但不确定性给予学生更多学习的权利和机会,有益于培养学生的创新能力[1],这对即将进入高校学习的学生而言,是一种不可忽视的教育.
2)近似计算与智能化紧密结合,拓宽了数学应用的广泛性.在科学与工程上常遇到求方程的解,但方程的精确解或不可利用,或求精确解的成本很高,因此我们常常考虑其满足一定精确度的近似解.计算机的发展为数学的发展提供了巨大的帮助,使得近似计算方法作为一种科学方法发展起来.
3)牛顿法“以直代曲”,是导数应用价值的生动体现.著名建筑设计师高迪曾说:“直线属于人类,而曲线属于上帝.”牛顿法体现了对曲线的巧妙处理.与“二分法”相比,牛顿法具有近似指向鲜明、智能依赖更低的独特作用.该法求方程近似解时只用到一阶导数值,且收敛速度较快,具有易用、适应性广、高效的特点,被广泛推广应用于求方程的近似解,具有很强的可扩展性,是数学应用上的一大法宝,作用无可替代.
牛顿法的核心是以切线的零点近似代替曲线的零点,需借助图像直观体现,才能更好领悟其蕴涵的思想;另一方面,要领会牛顿法需理解其运算思路,掌握运算步骤,提炼算法.此课题充分渗透和发展高中生的两大数学学科核心素养:直观想象和数学运算.
2 基于教材与学情的思考
本节课是人教A版《数学(选修2-2)》第一章第二节“导数的计算”中的“探究与发现”内容,属知识拓展类课程.课前学生已能理解函数的零点与方程的根的关系,会用二分法求方程的近似解,会利用导数求曲线的切线方程.高一学生已学习信息技术,理解计算机程序运行的一些基础原理,会读算法程序框图,选考技术的学生能编写简单的算法程序.教材介绍了导数的概念、计算、几何意义等,为牛顿法提供了理论和实践的基础.本节课除详细介绍牛顿法的基本思想外,还要在对比基础上突出牛顿法的优点.
存在的困难:一是学生对近似解的接受态度,学生已习惯求精确解;二是运算,要理解牛顿法就要体验该法的运算过程,但牛顿法运算繁琐,易望而生畏,若运算全依托计算机解决,学习感受单薄,不容易留下深刻印象.
3 教学目标设置
根据以上分析,制定本节课的教学目标为:
1)借助信息技术手段,运用数形结合思想,详细探究牛顿法的基本内涵及蕴涵的思想方法,提升直观想象核心素养;
2)了解用牛顿法求方程近似解的发生、发展过程,掌握牛顿法公式、运算原理,发展数学运算核心素养;
3)通过对比感悟牛顿法的优缺点,突出牛顿法的重要意义.
教学重点牛顿法的发生、发展过程,理解牛顿法的基本内涵.
教学难点“以直代曲”思想的自然呈现、逼近思想的渗透及精确度公式的解释.
4 教学策略分析
依据前面的分析,采用以下4种方法突破教学重点和难点:
1)回顾二分法求方程x2-2=0的近似解,采用学生熟知但未引起注意的问题激发学习兴趣.设置情境联系由牛一律过渡到牛顿法,之所以要联系牛一律,是因为牛顿法中的“切线”与牛一律有着非常紧密的联系,渗透“以直代曲”思想.
2)几何画板在作图上有着独特的优势,是数形结合的有力工具.通过几何画板呈现,让学生亲历“作切线”的过程和反复“作切线”的原因,深刻领会切线与x轴交点的横坐标逐步逼近函数零点的过程,形成算法.
3)利用Excel表展示不断变化初始值带来的影响,思考精确度的解决办法.
4)通过分析、讲解、对比等过程,加深对牛顿法的理解,感悟优缺点.
5 教学过程
5.1 相似情愫,重温“二分法”
问题1求方程x2-2=0的解.
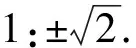
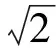
生2:1.414 2.
师:能多说几位小数吗?
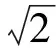
师:通过什么方法可以求方程的近似解?
生3:二分法.
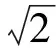
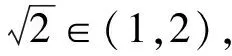
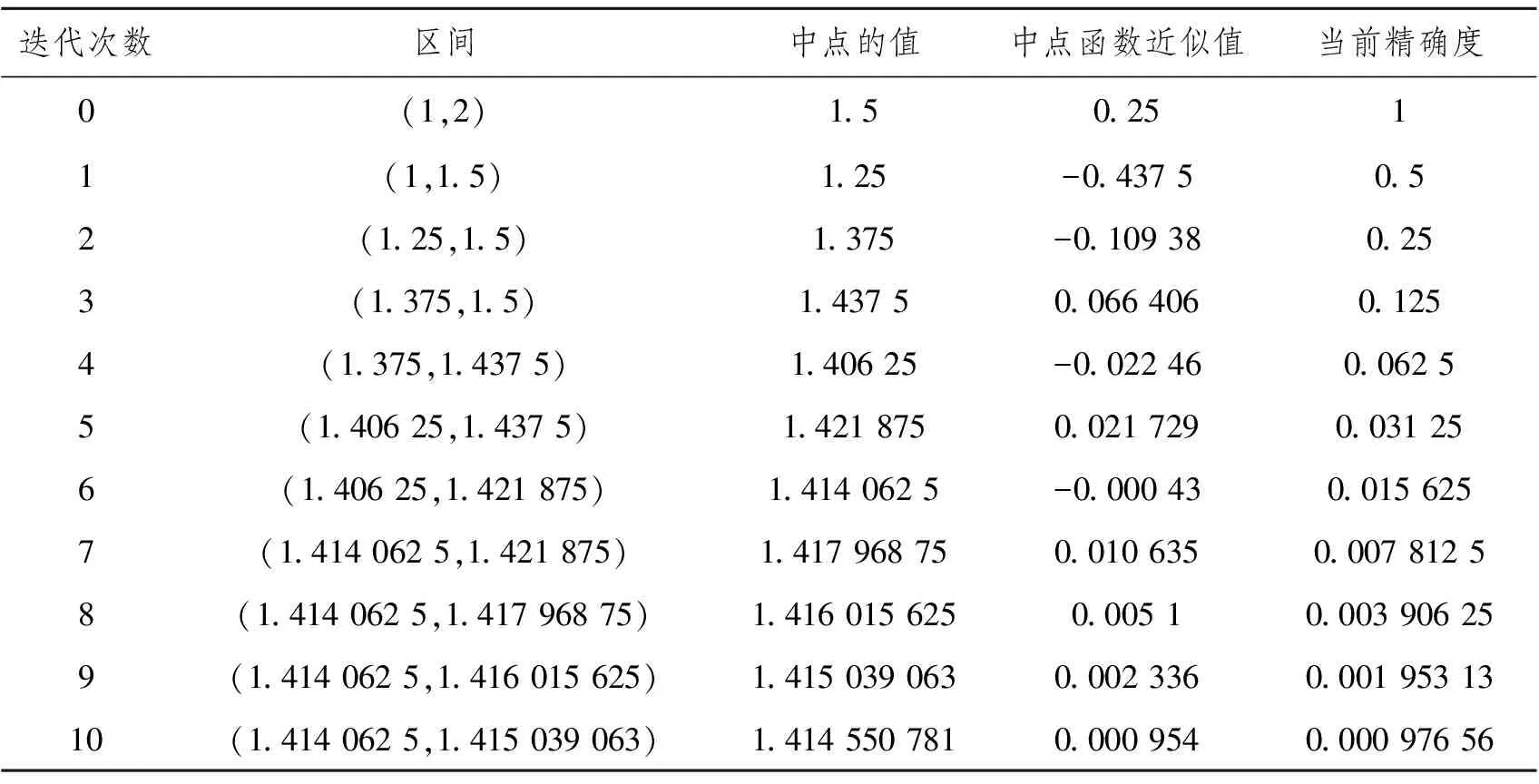
表1 二分法求解过程
由于ε=0.001,因此方程的近似解可取为1.414 062 5.
5.2 以直代曲,探秘“牛顿法”
师:求方程的近似解还有其他方法吗?现假设有一个物体A在刚才研究的函数f(x)图像上运动(切换到几何画板),当运动到某一点时,物体A的所有外力突然消失了,接下来物体A将做什么运动?
生4:匀速直线运动.
师:物体A的运动轨迹将在一条直线上,这条直线与函数f(x)图像有什么关系?
生5:相切.
设计意图以牛顿第一运动定律为切入点,自然地引出“切线”话题,目的在于实现“以直代曲”.
师:设这条切线与x轴的交点横坐标为x1.
问题3你能求出x1吗?
提示:1)要求出x1,需先写出f(x)在点A处的切线方程;2)要写出切线方程,就要先知点A的横坐标;3)设点A的横坐标为x0.
学生活动1)请学生写出函数f(x)在点A处切线的点斜式方程,并求出x1的值.2)选派学生在黑板上展示解答情况:
y-f(x0)=f′(x0)(x-x0),

不妨取x0=1,借助计算器,可得x1=1.5.
师:近似效果好像不差,但我想精确度再高一点,有改进办法吗?
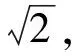
师:图1中尽管x1的精确度不高,但与选取的初始值x0比起来,明显更逼近r.如果要求一个精确度更高的近似解,可否把x1利用起来?
生7:求函数f(x)在x1处的切线方程,再求出切线与x轴交点的横坐标.
师:设求出的横坐标为x2,你能说明x2比x1更好吗?
生8:应该可以.
师:那我们来仔细观察一下.
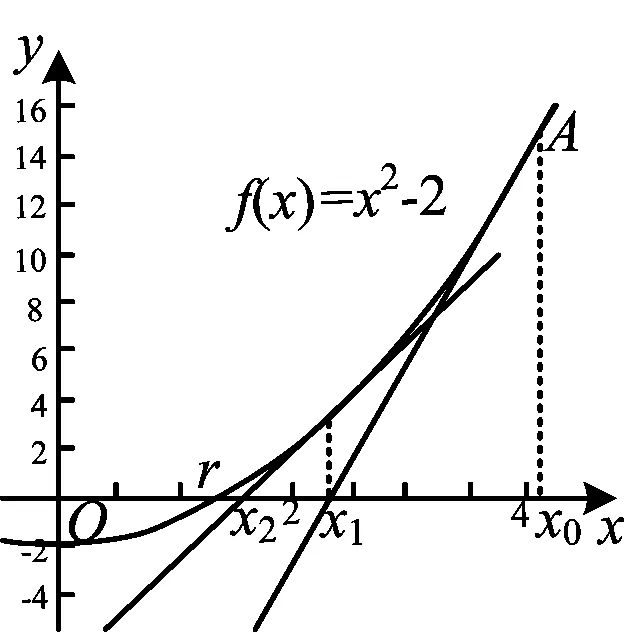
图1
(借助几何画板继续作x1处的切线,发现x2确实比x1好,如图1.)
师:参照求x1的过程,请大家用x1表示x2.
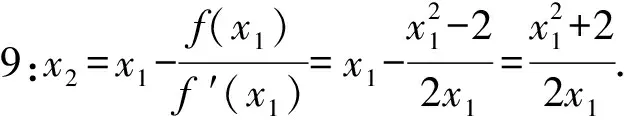
(借助计算器,若x0=1,可得x1=1.5,x2≈1.416 67.)
5.3 精雕细琢,优化“操作链”
师:那么x2作为r的近似解就可以了吗?
生10:不行,x2有可能误差还是太大.
师:那该怎么办?
生11:继续求f(x)在x2处的切线方程,再求出切线与x轴交点的横坐标x3.
师:很好,也许x3还不满足要求,但多求几次精确度总会更好,经多次重复,得到一列数:x0,x1,x2,x3,…,xn,从图像上可知这一数列越来越逼近r.
问题4xn与xn-1之间是否有关系?
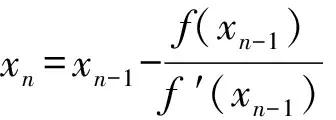
生12:是.
师:借助此递推式求近似解的方法就称为牛顿法.该递推式的得出借助了导数工具,因此牛顿法实质就是用导数方法求方程的近似解.该递推式称为牛顿法公式,要使公式有意义,f′(xn-1)的值可否为0?
生13:不可以.
师:那f(xn-1)=0呢?
生14:精确解求出来了.
师:牛顿法可以求出准确解.通过刚才的研究我们发现xn可能有无数多个,数不在多,够用就行.
问题5xn满足什么要求才能作为r的近似解?
生15:当|f(xn)|的值小于事先给定的一个精确度时,xn可作近似解.
生16:当|xn-xn-1|的值小于事先给定的一个精确度时,xn可作近似解.
师:现利用计算机技术(Excel表),如表2,先仔细观察数据变化,再思考如何定义更合理.
表2xn,f(xn)数据变化
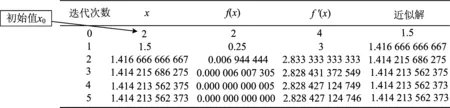
操作说明x0取0.5,1,2,5,10等值,仔细观察xn,f(xn)数据的变化,数据不够就下拉几行,会自动生成.
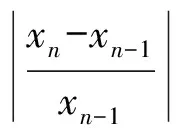
5.4 比较对照,体悟“先进性”
师:就算初始值x0偏离准确解比较远,牛顿法也能很快求出精确度比较高的近似解.在科学与工程上常遇到求方程的解,但方程的精确解或不可利用,或求精确解的成本很高,常考虑其满足一定精确度的近似解.通过这个例子我们发现利用牛顿法求方程近似解非常高效,应用广泛.
5.5 尝试纠偏,聚焦“初始值”
例1利用牛顿法求方程x3+2x2+10x-20=0的近似解,精确度z=0.001.
PPT展示基本步骤,提供答题范本如下:
解令f(x)=x3+2x2+10x-20,则
f′(x)=3x2+4x+10,
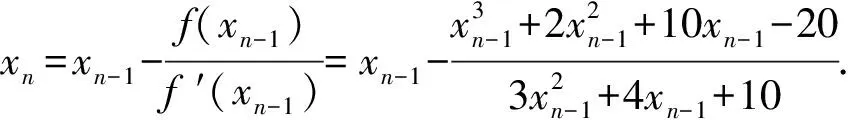

第二步:____________.
师:请大家选一个x0,借助计算器,根据示范的步骤算出符合精确度要求的近似解.
从学生中选出初始值分别为1和2的解答,并在备好的计算机程序上给学生检验一遍,另选定一个初始值4,得到以下表3:
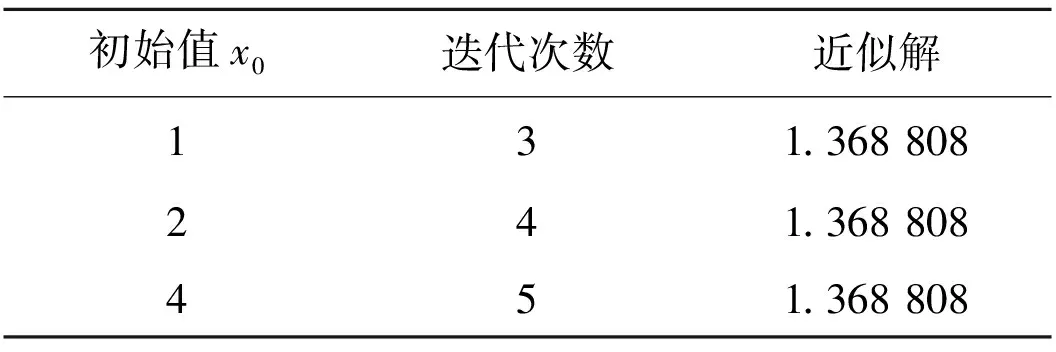
表3 不同初始值的迭代次数
问题6不同的初始值对求方程的近似解有影响吗?如果有,影响在什么地方?
结论影响在迭代次数,初始值越接近零点越好,因此用牛顿法求方程的近似解时要先对零点作估计.
师:大家觉得利用牛顿法运算有何特点?
生17:运算繁琐.
设计意图先统一解答格式,避免杂乱无章的解答浪费学生宝贵的时间.通过实例训练,感受牛顿法运算的特点,理清基本步骤,加深对牛顿法的认识.
5.6 提炼算法,达成“机械化”
师:既然牛顿法的运算比较繁琐,为何不把运算问题交给计算机解决,刚才的小程序是怎么编出来的呢?我们不妨先提炼牛顿法的算法.
提炼牛顿法的算法并展示框图.
1)牛顿法求方程近似解的基本步骤:
第一步,给定初始值x0和精确度z0;
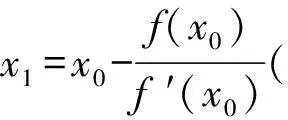
2)展示框图.
设计意图算法精炼地表达了牛顿法,达到了化繁为简、深入浅出、为生减负的目的.
师:运算的问题可由计算机代劳,由于迭代次数大大减少,牛顿法运算效率突出,优势明显,在科学和工程中有着广泛的应用.希望同学们努力学好数学,为投身中华民族伟大复兴打下坚实的数学功底.
6 教学说明与反思
6.1 为何强调用牛顿法求近似解
因为牛顿法算法简洁,运算高效,应用广泛,作用无可替代,所以牛顿法是珍贵的数学方法.学习牛顿法,绝不是仅为了求近似解,此法“高端”,让学生感受到数学在科学工程上的应用,认识到数学的重要性;牛顿法蕴涵着珍贵的数学思想,有利于锻炼学生理性的思维品格、创新能力,发展学生的数学核心素养.
6.2 “以直代曲”关键问题的思考起点
“以直代曲”的思想早已出现,古代著名数学家刘徽和祖冲之“化圆为方”计算圆周率就运用了“以直代曲”思想,意在方便求圆的面积,无需求出直线解析式.牛顿法中的直线肩负着两个重要任务:一是把复杂的曲线转化为简单的直线;二是借助直线求出与x轴交点的横坐标,达到求近似解的目的.
章建跃老师告诉我们:教学要返璞归真,要让学生参与知识的生成和发展过程,在教学中培养学生的创新精神和实践能力[2].笔者一直在思考,牛顿因何想到如此“神奇”的直线?1666年初,牛顿创立了三大运动定律,并着重从运动学角度研究微积分,1671年完成了与牛顿法相关的《流数法》.牛一律告诉我们:一个运动的物体,在某一时刻如果外力消失,物体将做匀速直线运动,这条直线就是原来曲线的一条切线.基于以上理由,牛顿第一运动定律为发现牛顿法作了一些铺垫.从学生熟知的牛一律引出“切线问题”,凝聚着我们对数学历史发展的思考,渗透了数学文化,让课堂变得生动有内涵,体现了自然哲学的数学原理.
6.3 迭代和精确度问题
这两个问题也是本堂课难以突破的地方.迭代和精确度是相辅相成的,迭代是为了提高近似解的精确性,精确度是迭代的动力和休止符.
如何引导学生发现迭代?是因为无法保证x1满足精确度要求,这点一定要让学生发现;然后才产生第二个问题:如何提高近似解的精确度?这与二分法有了联系.细究方法均具有“模式化”特点,有利于机械化解决数学问题[3],算是数学中的辩证和统一吧.
精确度该如何定义?学生肯定很难想到教材上的答案,因为多种定义都很合理,学生的认知很难发现缺陷和不足.因此精确度问题不要过多纠缠,说清楚就好.
以上3点是笔者对这堂课几个关键问题的反思.本节课知识容量大,很难顾及到教学的方方面面,但把握以上几点,相信课堂教学很多难题会迎刃而解.
