动态几何 以静制动 克难致胜*——例说立体几何“动态”题型解题策略

●

(三门第二高级中学,浙江 三门 317100)

“动态”充满着神奇，孕育着创造．动态问题渗透着运动变化的观点，是立体几何的一大难点，又是高考的一大亮点；这类题涉及的知识点多，覆盖广面，渗透着主要的数学思想方法，能全方位地考查学生的基础知识、基本能力、数学素养、数学发展潜能等．学生在解决这类问题时，总存在着一定的心理困惑或思维障碍.解决好立体几何的“动态”题型，不仅可以提高学生分析和解决问题的能力，而且可以提高学生的数学应用能力和综合解题能力.

所谓“动态”立体几何题,是指在点、线、面运动变化的几何图形中，探寻点、线、面的位置关系或进行有关角与距离的计算.由于这类题情景新颖、解法灵活、极富有思考性和挑战性，能更好地考查学生的空间想象能力和思维能力,因此成了高考的热点内容之一.我们知道,动与静是矛盾的两个方面,动中有静,静中有动.

立体几何中的“动态”问题就变化起因而言大致可分为两类：一是平移；二是旋转.就所求变量而言可分为3类：一是相关线、面、体的测度；二是角度；三是距离.立体几何动态问题的解决需要较高的空间想象能力与化归处理能力，在各省市的高考选择题与填空题中也时有出现.在解“动态”立体几何题时,如果我们能努力探寻运动过程中“静”的一面，动中求静，往往能以静制动、克难致胜.下面是笔者对破解立体几何动态问题的一些思考，以期抛砖引玉.

1 去掉枝蔓见本质——大道至简

在解决立体几何中的“动态”问题时，需从复杂的图形中分化出最简单的具有实质性意义的点、线、面，让几何图形的实质“形销骨立”，即从混沌中找出秩序，是解决“动态”问题的关键.

图1

例1如图1，直线l⊥平面α，垂足为O.正方体ABCD-A1B1C1D1的棱长为2.点A是直线l上的动点，点B1在平面α内，则点O到线段CD1中点P的距离的最大值为______.

分析从图形分化出4个点O，A，B1，P，其中△AOB1为直角三角形，固定AOB1，点P的轨迹是在与AB1垂直的平面上且以AB1的中点Q为圆心的圆，从而

当且仅当OQ⊥AB1，且点O，Q，P共线时取到等号，此时直线AB1与平面α成45°角.

2 极端位置巧分析——穷妙极巧

在解决立体几何中的“动态”问题时，对于移动问题，由图形变化的连续性，穷尽极端特殊之要害，往往能直取答案.

例2在正四面体A-BCD中，E为棱BC的中点，F为直线BD上的动点，则面AEF与面ACD所成二面角的正弦值的取值范围是______.

分析本例可用极端位置法来加以分析.

先寻找垂直：记O为△ACD的中心，G为OC的中点，则BO⊥面ACD，EG⊥面ACD.如图2，过点A，E，G的平面交直线BD于点F.此时，面AEF与面ACD所成二面角的正弦值为1.

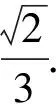
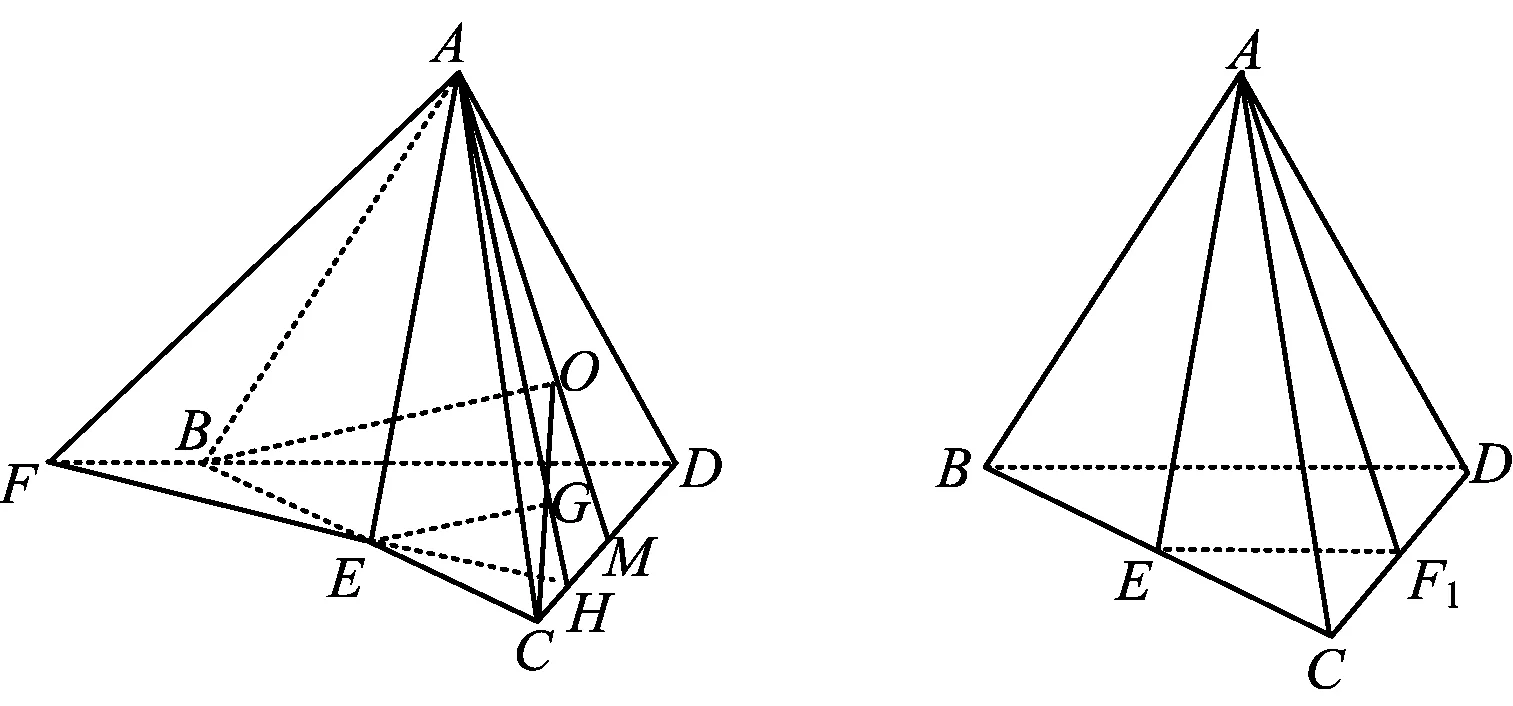
图2 图3

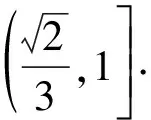
3 用法向量定平面——定海神针

在解决立体几何中的“动态”问题时，有关角度计算问题，用法向量定平面，可将线面角或面面角转化为线线角.

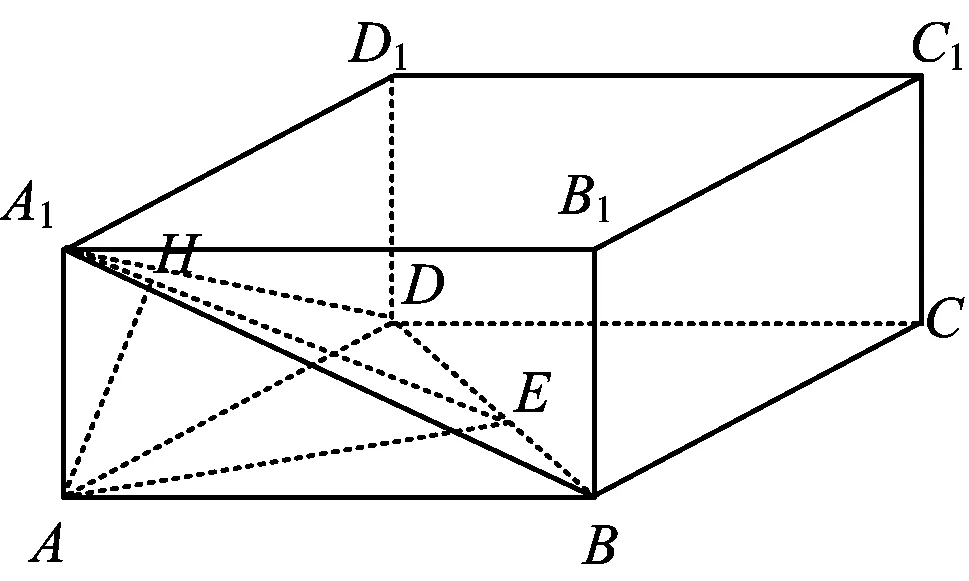
图4

4 锁定垂面破翻折——独挡一面

在解决立体几何中的“动态”问题时，对于翻折或投影问题，若能抓住相关线或面的垂面，化空间为平面，则容易找到问题的核心.

例4如图5，在等腰Rt△ABC中，AB⊥AC，BC=2，M为BC的中点，N为AC的中点，D为线段BM上一个动点(异于两端点)，△ABD沿AD翻折至B1D⊥DC，点A在面B1CD上的投影为点O，当点D在线段BM上运动时，以下说法错误的是

( )

A.线段NO为定长

C.∠AMO+∠B1DA>180°

D.点O的轨迹是圆弧

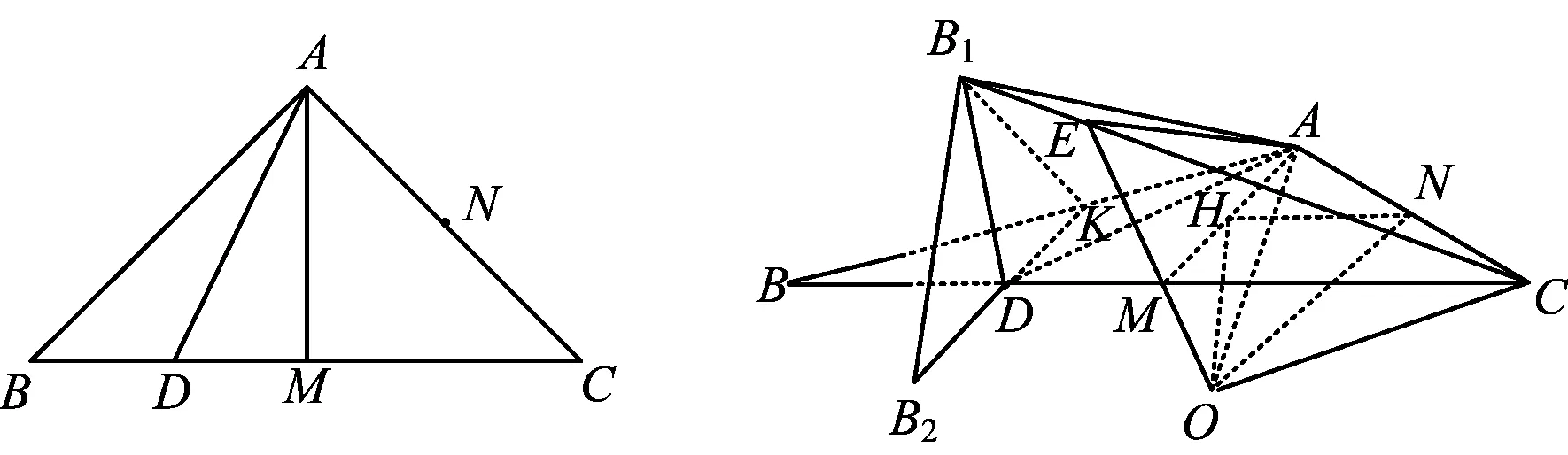
图5 图6

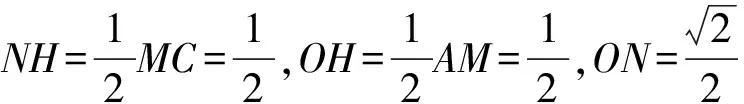
∠B1DB2<180°-∠B1DA，

得

∠B1DK>∠B1DA，

于是

∠AMO+∠B1DA<180°.

故选C.

5 觅得定值明轨迹——动中有静

在解决立体几何中的“动态”问题时，探寻变化过程中的不变关系，是解决动态问题的常用手段.

例5如图7，已知线段AB垂直于定圆所在的平面，B，C是⊙O上的两个点，H是点B在AC上的射影，当点C运动时，点H运动的轨迹是

( )

A.圆 B.椭圆

C.抛物线 D.不是平面图形

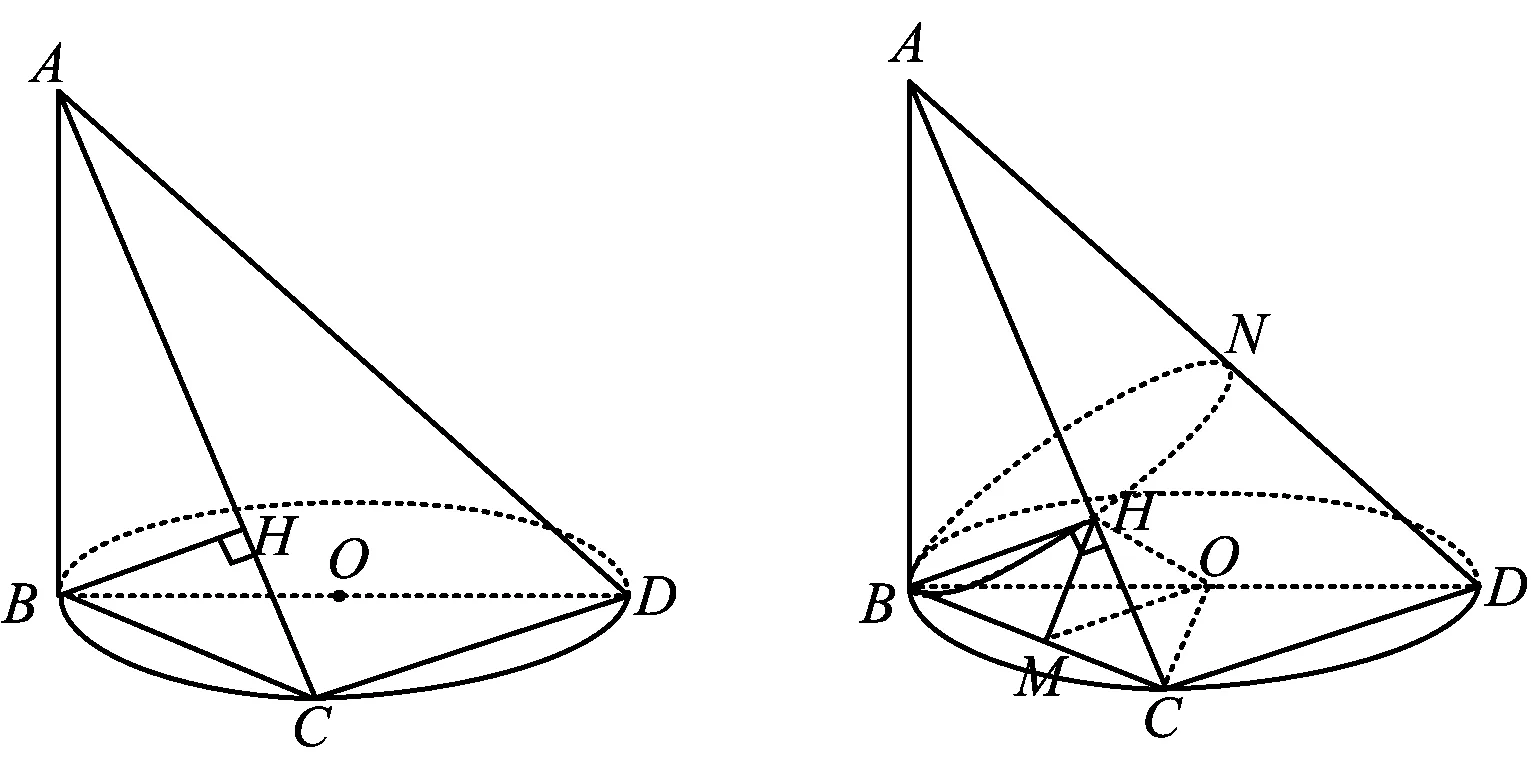
图7 图8

分析如图8，设⊙O的半径为r，取BC的中点M，则

OM⊥BC，MH=MC.

因为AB⊥面BCD，所以BC是AC在面BCD上的射影，从而OM⊥面ABC，得OM⊥MH，于是

OH2=MO2+MH2=MO2+MC2=r2，

即OH=r，亦即动点H在以O为球心、r为半径的球面上.又因为BH⊥AD，B为定点，所以动点H又在过点B且垂直于直线AD的定平面上,故点H运动的轨迹是圆.

6 构建函数求最值——以数解形

在解决立体几何中的“动态”问题时，对于一些很难把握运动模型(规律)的求值问题，可以通过构建某个变量的函数，以数解形.

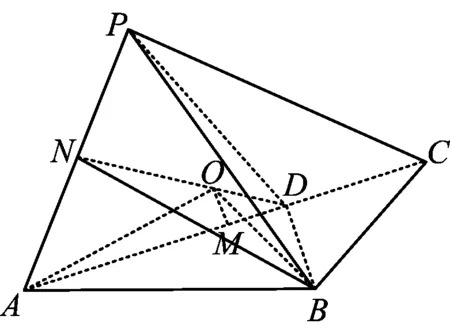
图9

例6如图9，在△ABC中，AB=BC=2，∠ABC=120°.若平面ABC外一点P和线段AC上一点D，满足PD=DA，PB=BA，则四面体P-BCD的体积的最大值是______.

(2016年浙江省数学高考理科试题第14题)

分析设M，N分别为AC，AP的中点，因为BA=BP=BC，PD=DA,所以点B在平面PAC上的射影为△PAC的外心O，且点O在直线ND上.又因为AB=BC=2，∠ABC=120°，所以

当且仅当点M与点D重合时取到等号.因此，四面体P-BCD的体积为

此时点O，M，D重合,即点D为AC的中点，且平面PBD与平面ABC垂直相交于BD.

总之，解立体几何动态问题的过程实质是数学建模的过程，是创新的过程．方程、函数和图形变换是基础，因此夯实基础是解决此类问题的关键．化整为零的思想、转化思想、数形结合思想、函数思想、分类讨论思想等是解决立体几何动态问题的最佳策略．真正破解动态立体几何问题，需要整体把握动态变化过程，更需要深厚的空间想象之内功．如果说招式是术，那么内功就是修行，即不断积累知识与技巧、经验与经历．所谓模式就是在特定环境下人们解决某类重复出现问题的一套成功或有效的解决方案．在平时教师要引导学生作适当的变化和拓展训练，开阔视野，培养动态思维，锻炼数学思想，积累解题经验，提高应变能力，创造性地使用所学知识，如此才能从容应对新的动态问题．