含单纯凹陷薄壁不锈钢燃气管道的韧性损伤程度分析*

2018-11-30肖洁文黄云飞

中国安全生产科学技术 2018年11期

伍颖，邹荣，肖洁文，黄云飞

(西南石油大学土木工程与建筑学院，四川成都610500)

0 引言

当前，薄壁不锈钢管在燃气工程中的普及率越来越高。薄壁不锈钢燃气管道技术不断完善和改良，日趋成熟，其优良的综合性能受到了国内外市场的肯定和认可[1]。随着薄壁不锈钢燃气管道的大量敷设，管道的安全问题引起了广泛关注。凹陷是油气管道机械损伤中最为常见的缺陷形式，对管道的运行寿命有相当大的影响[2-3]，可能由施工机械的不正确开挖、管道上方落下的岩石的冲击、管道下方的岩石或坚硬物影响，以及其他事故[4-6]等因素导致。国外针对凹陷管道的完整性评价开展了相关研究工作，并制定了一系列的标准，如加拿大管道设计标准CSA Z662-15[7]、美国机械工程师协会ASME B31.4─2012[8]和B31.8─2016[9]，规定管道的凹陷深度不能超过管道直径的6%。然而在实际工程中发现，单纯基于深度的评价准则已不能满足工程的应用[10]，需要结合更多参数来评估含凹陷缺陷的管道。国内方面，伍颖等[11]、马欣等[12]开展了凹陷管道的相关研究工作，采用非线性有限元分析方法，在不同情况下对2种类型的单纯凹陷管道的韧性损伤及剩余强度等进行了研究，并取得了相应的研究成果。

已有的研究都针对大尺寸油气管道，对于小尺寸的薄壁管道还没有相关的研究先例。前人针对大尺寸油气管道研究得出来的结论与规律是否在小尺寸薄壁钢管上也同样适用是未知的。因此，有必要针对小尺寸薄壁管开展相关研究工作。本文在Oyane韧性断裂准则的基础上，采用有限元软件ABAQUS建模，针对含单个单纯凹陷(凹陷区域内没有其他缺陷如沟槽、裂纹、焊缝等的平滑凹陷，且壁厚没有减少，只有曲率发生了变化[13])的薄壁不锈钢燃气管道进行韧性损伤程度分析，得到凹陷深度和管道损伤程度的具体数学关系式，以及参数变化对管道损伤程度的影响规律。

1 Oyane韧性断裂准则

韧性断裂准则大多是建立在损伤思想的基础之上的，这些断裂大致可以分为2类：第1类是基于宏观半经验半理论基础上的，第2类是建立在微观基础之上的。基于以上2类准则，对于损伤的研究主要有宏观方法和微观方法[14]。从微观角度来说，材料在大变形下会出现损伤，伴随着微观空穴的长大和聚合，直至许多空穴聚集在一起产生裂纹，引起韧性断裂，所以韧性断裂准则也是1种损伤断裂准则。Mc-Clintock，Cockcrof & Latham和Brozzo等人都提出了损伤断裂准则[15]，但这些准则均未考虑金属大变形的影响，在实际应用中有较大局限性。Oyane 准则考虑到静水应力可以抑制或加速韧性破坏，能定量的表示瞬时的损伤状态。

本文选用Oyane韧性断裂准则来分析在不同情况下薄壁不锈钢燃气管道凹陷深度与管道受损程度之间的关系。

Oyane韧性断裂准则是1种用于可压缩材料的韧性断裂准则[16]。该准则体现了静水压力对材料内部空洞增长或者闭合的影响，甚至能够模拟裂纹增长的影响。该准则的表达式如下式所示[17]：

(1)

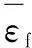
F(σy-σz)2+G(σz-σx)2+H(σx-σy)2+

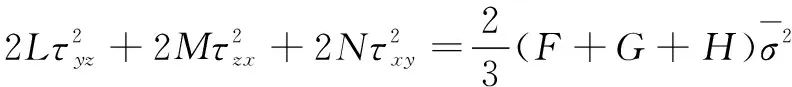
(2)

(3)

(4)

(5)

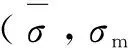
2 有限元建模

对管径为DN=40 mm，壁厚t=1 mm的钢管做拉伸试验。管材的力学性能为：弹性模量E=2.06×105MPa，泊松比n=0.3，屈服强度σS=375 MPa，抗拉强度Rm=712 MPa，厚向异性系数为1，延伸率为40.2%。

管道模型及施痕物模型都采用ABAQUS有限元软件中的C3D8R实体单元，采用C3D8R单元进行有限元计算时，在弯曲荷载下不易发生剪切自锁[20]。

由于管道模型的荷载条件存在对称性，故只建立1/4管道模型进行有限元分析计算。在编号A面施加Z向对称约束，在编号B，C面施加X向对称约束，在编号D面施加完全固结约束。假设外界对管道底部的约束是刚性的并沿管道全长，所以对管道底部约束其Y向自由度，并沿管道环向120°进行约束。图1为管道模型及边界条件示意图。

球形施痕物沿管道轴线按压管道形成凹陷，凹陷的大小与球形施痕物的尺寸以及加载深度密切相关。在实际情况中，大部分的凹陷属于非约束凹陷，即当管壁上形成一定凹陷深度以后，施痕物就被移开了。对薄壁不锈钢管道模型施加凹陷以及移除施痕物的有限元分析步骤如图2所示。

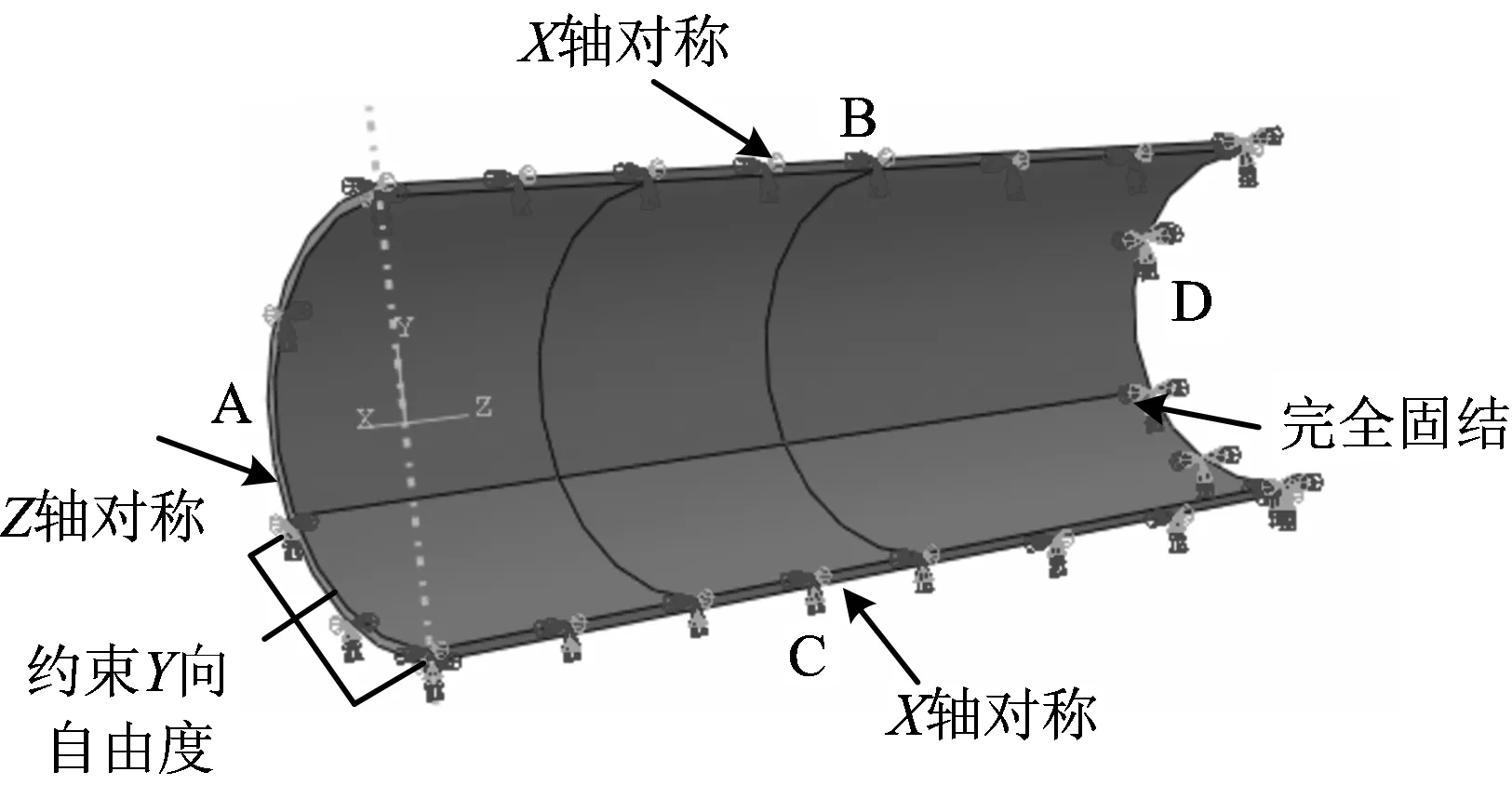
图1 管道模型及边界条件示意Fig.1 Pipeline model and boundary condition diagram

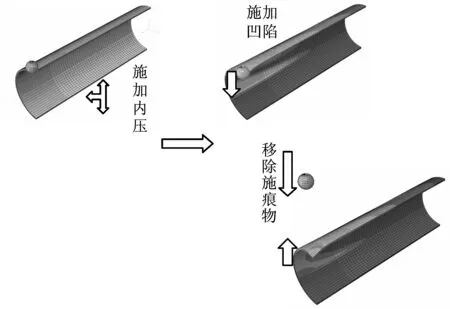
图2 有限元分析步骤Fig.2 The nite element analysis steps

3 单纯凹陷管道损伤程度分析

对管道模型分别施加不同深度的凹陷缺陷，可分析不同施痕物尺寸、不同管道尺寸以及不同运行内压情况下，凹陷深度与管道损伤程度之间的关系。

管道直径为D，mm；壁厚为t，mm；二者之比D/t表征管道尺寸；施痕物半径为r，mm；管道直径为D，mm；施痕物半径与管道直径之比r/D表征施痕物尺寸；管道运行内压为P，MPa；凹陷深度为d，mm；以下管道壁厚均采用1 mm进行研究。

3.1 应力应变结果分析

3.1.1 卸载前后应力结果分析

有限元模型中，D=40 mm，t=1 mm，r/D=0.15，d=4 mm，P=0 MPa。以该参数下建立的模型为例进行分析。施痕物卸载前后，凹陷区域内表面的Von Mises等效应力沿管道环向和轴向的分布如图3所示。

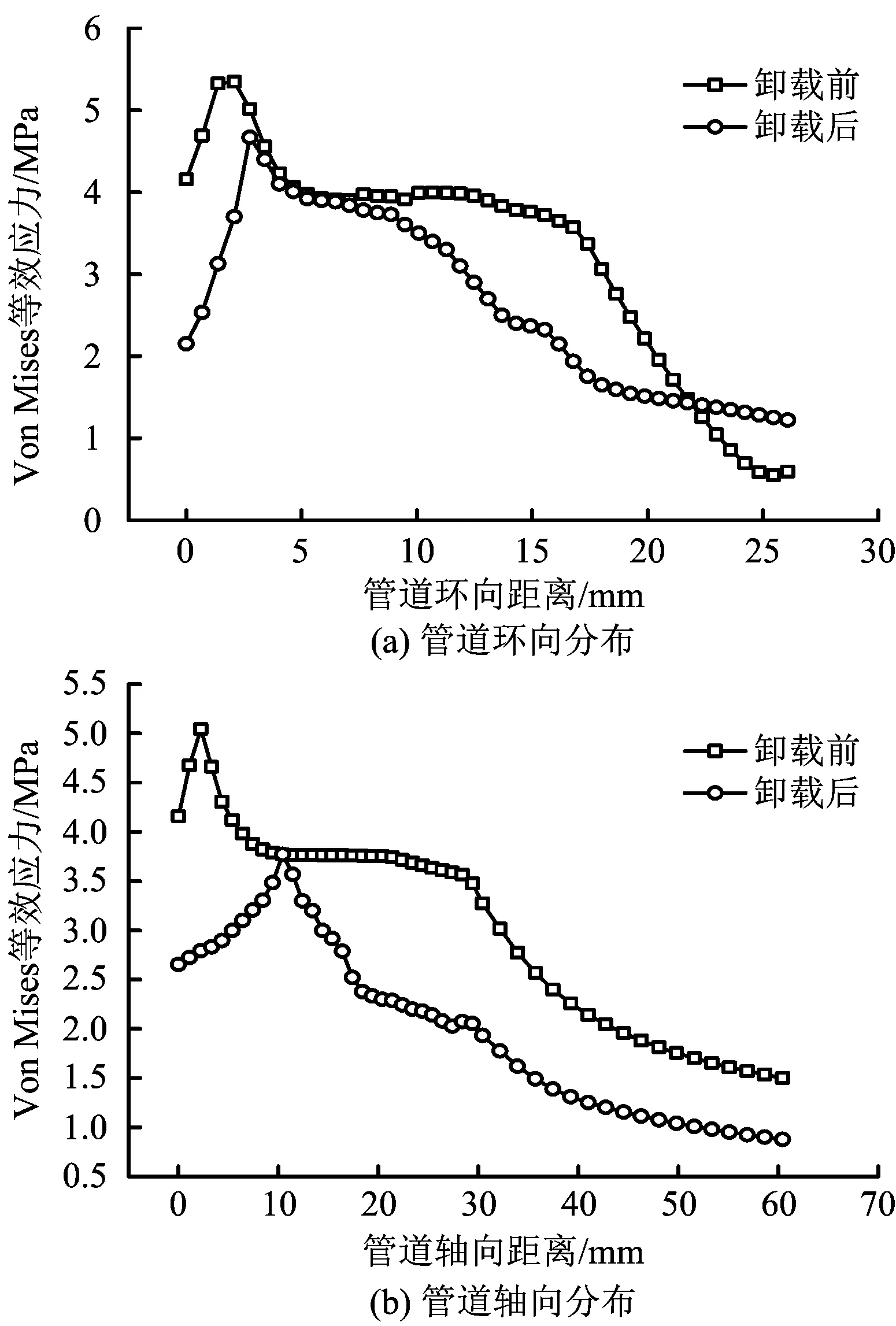
图3 施痕物卸载前后凹陷区域内表面的Von Mises等效应力沿管道环向和轴向的分布Fig.3 Distribution of Von Mises equivalent stress along the circumferential and axial directions of the inner surface of the concave region before and after unloading

从图3可以看出，该凹陷深度下，Von Mises等效应力最大值不在凹陷中心，而是在凹陷中心附近；Von Mises等效应力均小于卸载前的Von Mises等效应力；卸载后Von Mises等效应力最大值所在的位置与凹陷中心之间距离均大于卸载前其与凹陷中心之间的距离。这是因为施痕物移除以后管道由于自身弹塑性性质或内压的影响使管壁产生一定程度的回弹，从而导致局部应力集中区域从凹陷中心向边缘转移。由于管壁的回弹作用还导致施痕物卸载后凹陷区域内Von Mises等效应力最大值比卸载前小一些。

3.1.2 等效塑性应变分析

以D=40 mm，t=1 mm，r/D=0.15，凹陷深度d分别为1，3，5和7 mm的管道模型为例进行分析。

4种不同凹陷深度情况下，凹陷区域内Von Mises等效应变沿管道环向的分布情况如图4所示。

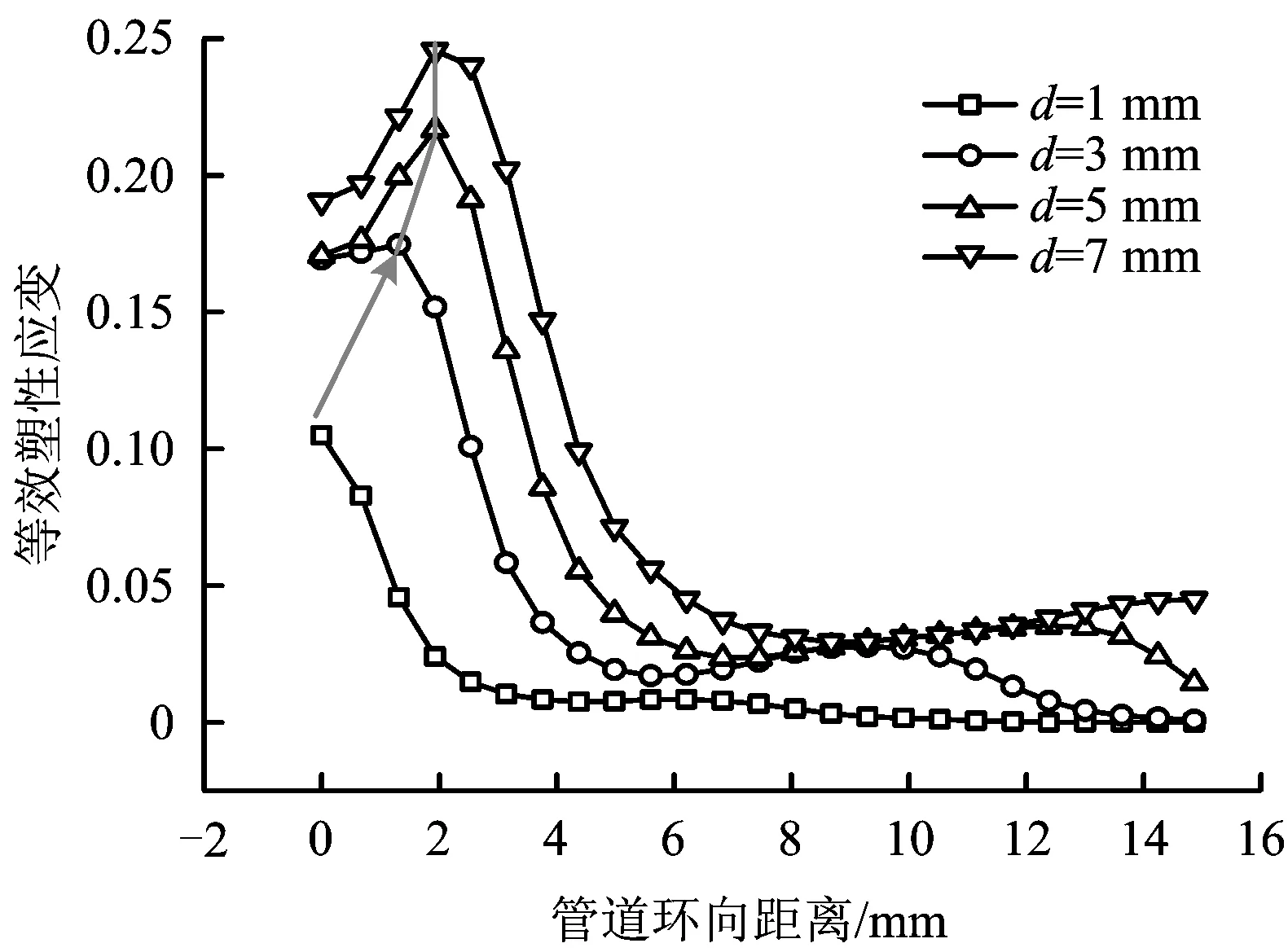
图4 不同凹陷深度下最大等效应变沿管道环向的分布情况Fig.4 Distribution of maximum equivalent strain along the circumferential direction of pipelines at different depths

从图4中带箭头的线条可以看出，最大等效塑性应变点的位置随着凹陷深度的增加从凹陷中心沿管道环向向外转移，即凹陷深度越大，最大等效塑性应变点距离凹陷中心越远。

3.2 施痕物尺寸

以管道D=40 mm，壁厚t=1 mm的薄壁不锈钢燃气管道作为研究对象，分析不同施痕物尺寸作用下凹陷深度与管道韧性损伤程度之间的关系，韧性损伤程度采用积分值I表示。管道模型的长度取直径的6倍，即L/2=3D；r/D值分别取0.1，0.15，0.2以及0.25；d取值分别为1，2，3，4，5，6，7和8 mm；假设P=0 MPa。

有限元计算结果显示，凹陷区域内最大的Von Mises等效应力点均位于管壁内侧，通过计算，该点积分值最大，其所在区域即为管道受损最严重的部位。说明管道形成凹陷以后，管道内表面的受损程度高于管道外表面。不同施痕物尺寸作用下，d与I之间的关系如图5所示。

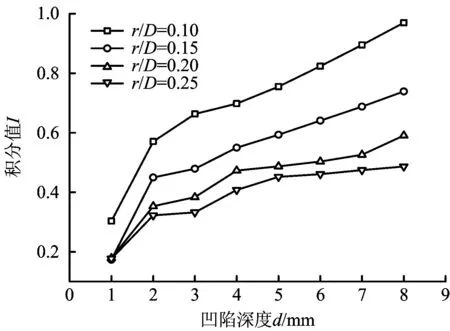
图5 不同施痕物尺寸作用下凹陷深度d与积分值I的关系Fig.5 Relationship between the d and the integral value I under different indenter size

从图5可以看出，当管径、壁厚为定值时，内压保持不变，在不同施痕物尺寸作用下，管道的损伤程度积分值I随凹陷深度d的增大而增大；当凹陷深度保持一定时，施痕物尺寸越大，对应的积分值越小，说明较大的施痕物有利于减小局部应力集中现象，从而降低管道的受损程度。

3.3 管道尺寸

D/t取值分别为25，32，40和50，其中，t=1 mm，P=0 MPa，r均取6 mm，d分别取1，2，3，4，5，6，7和8 mm。

当壁厚和施痕物尺寸为定值时，内压保持不变，在不同管道尺寸作用下，d与I之间的关系如图6所示。

图6 不同管道尺寸作用下凹陷深度d与积分值I的关系Fig.6 Relationship between the d and the integral value I under different pipeline size

从图6可以看出，当壁厚和施痕物尺寸为定值时，内压保持不变，在不同管道尺寸作用下，管道损伤程度积分值I随凹陷深度d的增大而增大；当凹陷深度保持一定时，管道尺寸越大，对应的积分值越小；当D/t=25时，由于施痕物尺寸相对于管道尺寸较大，所以积分值I随凹陷深度的变化幅度较大；当D/t=50，由于管道尺寸比较大，当d等于1 mm时，Von Mises等效应力最大值位于管道内表面的凹陷中心，而其他3种管道尺寸作用下Von Mises等效应力的最大值位于管道外表面的凹陷中心。因此，D/t=50作用下的损伤积分值I比D/t=32和D/t=40作用下对应的积分值大一些。

3.4 管道内压

目前的薄壁不锈钢燃气管道主要用于地上明设工程，适用于运行压力不大于0.2 MPa的新建、扩建、改建的地上燃气管道，中压设计压力0.2 MPa，低压运行压力：天然气2 000 Pa、液化石油气2 800 Pa，管道合理使用30 a。因此选用运行压力P分别取0，0.002，0.002 8，0.1和0.2 MPa时的管道作为研究对象，管道模型采用DN=40 mm，壁厚取t=1 mm，施痕物的半径r均取6 mm，凹陷深度d分别取1，2，3，4，5，6，7和8 mm。

当管道尺寸及施痕物尺寸为定值时，在不同运行内压作用下，凹陷深度d与积分值I之间的关系如图7所示。

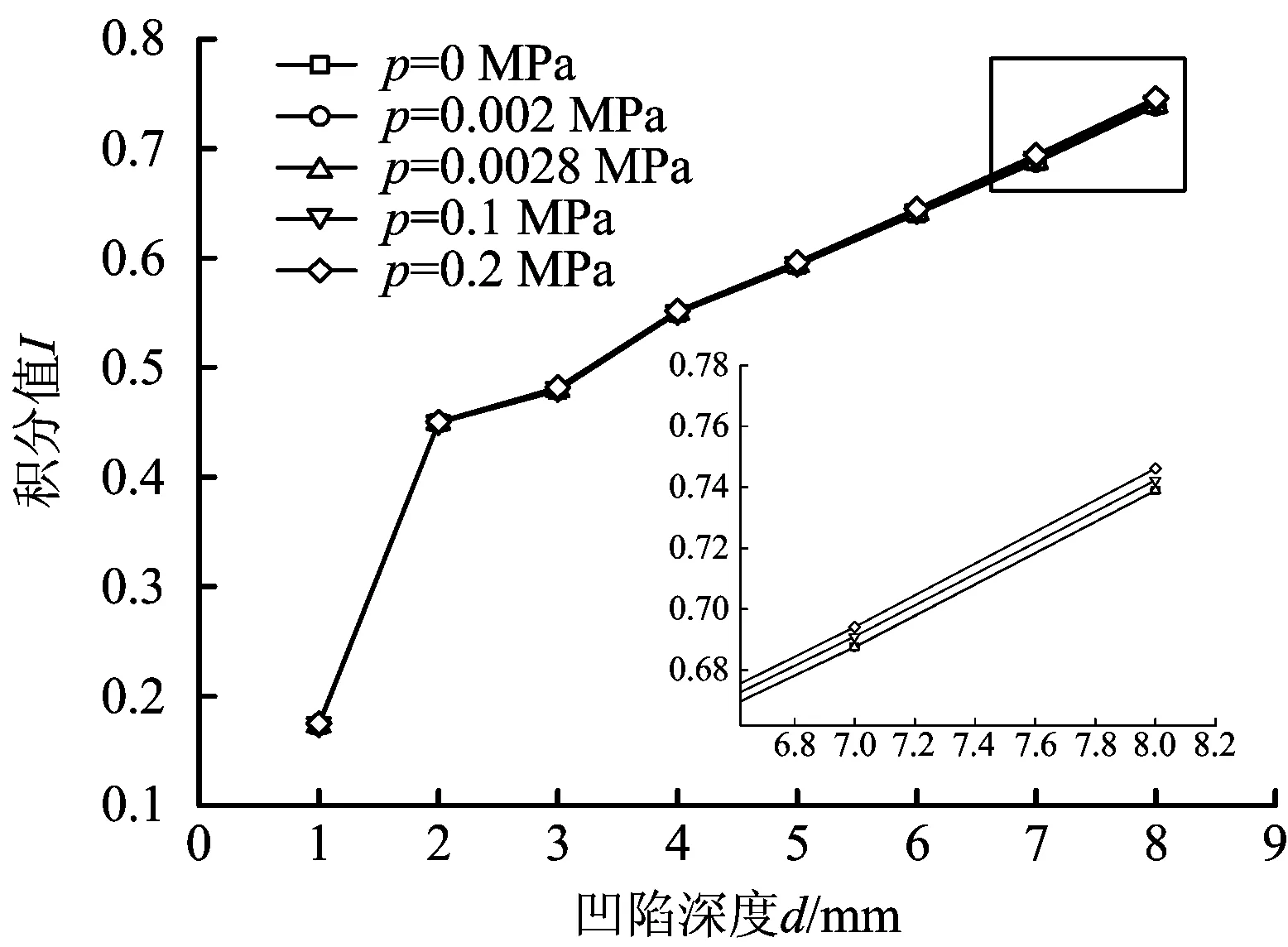
图7 不同运行内压作用下凹陷深度d与积分值I的关系Fig.7 Relationship between the d and the integral value I under different operating internal pressure

从图7可以看出，当管径、壁厚及施痕物尺寸为定值时，在不同运行内压作用下，管道的损伤程度积分值I随凹陷深度d的增大而增大；当凹陷深度保持一定时，由于薄壁不锈钢燃气管道属于中低压运行管道，且运行压力不能超过0.2 MPa，运行内压对积分值I的影响较小，可以忽略不计。通过局部放大图的观察，可以发现运行压力越高积分值I越大。