深入探究两类基本不等式问题的解题策略
2018-11-29陈后万
陈后万
(浙江省洞头区第一中学 325700)
基本不等式问题灵活多变、方法多样,常用方法就有:凑、拆、代换、去和留积、去积留和、消元等.所以对于基本不等式问题,还是要经常总结、归纳题型,寻找规律,探索合适方法.
类型一:已知Axy+Bx+Cy+D=0 (A≠0),求Ex+Fy或xy的最值问题
例1 (2016绍一中模拟)若正数x,y满足xy+x+2y=6,求x+y的最小值.
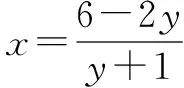
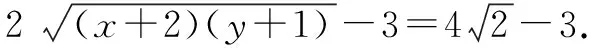
点评对于类型:已知Axy+Bx+Cy+D=0(A≠0),求Ex+Fy的最值问题.一般用消元法可以解决,可谓是通法,但转化过程有时计算量稍大.解法二(待定系数法)是能够解决一类问题的,前提是条件能够转化成(x+a)(y+b)=c(a,b,c>0).它充分体现了基本不等式的优点,计算量小,方法绝妙,让人惊叹.
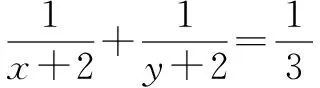
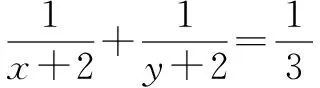

例3 (2012浙江卷)若正数x,y满足x+3y=5xy,则3x+4y的最小值是( ).
A. 245 B. 285 C. 5 D. 6


例4 若正数x,y满足2xy+x-y-1=0,则2x+y的最小值为 .
解法一(消元)略.
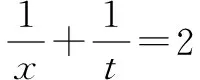
点评解法二中的换元法,技巧性比较强,目的是为了消去常数.这样,问题显然可以化归到例3类型问题处理.
总结:一般情况下,消元法、待定系数法、代换法可以解决类型一问题,具体应用还要看题目本身的系数特点.
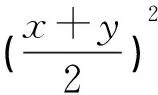
例5 (2011浙江高考)设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是 .
解∵4x2+y2+xy=1,∴(2x+y)2-3xy=1,



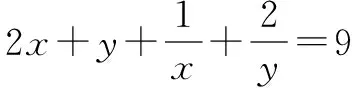
A.2 B.6 C.8 D.9
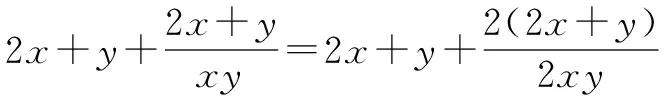
总结:基本不等式求函数最值(或值域)有着很多应用,极具简洁快捷功能.要熟练地求解基本不等式问题,主要靠平时善于总结、乐于总结,充分运用化归思想,抓住它的几条使用原则不放,构建基本不等式条件,高屋建瓴地使用基本不等式.
