对一道高考试题的本质探究
2018-11-29纪建灵吴宝树
数理化解题研究 2018年31期
纪建灵 吴宝树
(福建省泉州市第七中学 362000)
吴宝树,泉州市第七中学数学教师,中学一级教师,教育硕士.
2014年高考新课标高考数学卷Ⅱ的17题:已知数列{an}满足a1=1,an+1=3an+1.


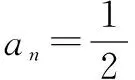
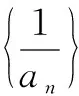
(2012广东高考)设数列n的前n项和为Sn,满足2Sn=an+1-2n+1+1,n∈N*,且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
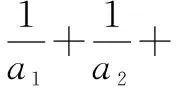


根据考查学生的需要,我们可以运用一些常见的试题改造的办法,通过改变试题背景或改变设问方式,编制出一些新的具有仿等比性质的数列试题,例如:
设数列an的前n项和为Sn,且满足2Sn=3an-4n.
(1)求数列{an}的通项公式;
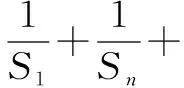
解析(1)an=2×3n-2.

