等差和等比数列交汇题目赏析

崔 文 侯宇虹

(1.山东省文登第一中学 264400;2.山东省威海市南海高级中学 264400)

侯宇虹，高级教师，文登区教学能手，注重高考数学教学研究，教学经验丰富.

高考中常见等差和等比数列交汇考查的题目，此类题目因涵盖知识点多，综合性强，对化归转化能力、运算求解能力要求较高，备考时需要多加重视.

一、等差数列中的等比数列

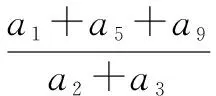
分析根据a2，a4，a8成等比数列可以求出等差数列an中首项a1与公差d之间的关系，然后进行计算.

答案：3.

点评考查等比数列的定义，等差数列的通项公式.

二、等比数列中的等差数列

例2 在等比数列an中，已知a1=1,a4=8，若a3,a5分别为等差数列bn的第2项和第6项，则数列bn的前7项和为( ).

A. 49 B. 70 C. 98 D. 140

分析分析出等比数列an的通项公式，就可以得到等差数列bn的通项公式，然后求和.

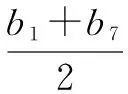
答案：B

点评考查等差、等比数列的通项公式，等差数列中序号与项之间的关系：若m+n=p+q，则am+an=ap+aq.

例3 (2017全国Ⅰ，文17)记Sn为等比数列an的前n项和，已知S2=2，S3=-6.

(1)求an的通项公式；

(2)求Sn，并判断Sn+1，Sn，Sn+2是否成等差数列.

分析(1)项数较少，可利用通项公式直接求出；(2)三项成等差数列，用“等差中项法”判断.

故{an}的通项公式为an=(-2)n.

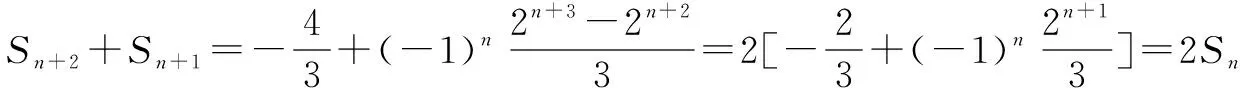
点评数列的通项公式或前n项和，部分项仍可成等差或等比数列，借此考查等差、等比数列的判定.

三、正项等比数列取对数构造等差数列

例4 设an是公比大于1的等比数列,Sn为数列an的前n项和,已知S3=7，且a1,a2,a3-1 成等差数列.

(1)求数列an的通项公式；

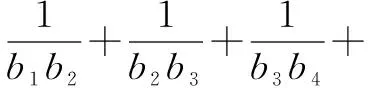
分析(1)利用等差、等比数列的性质求出数列an的通项公式；(2)因为an为等比数列，所以bn=log4a2n+1为等差数列，然后求和.

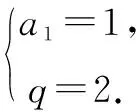
(2)由(1)得a2n+1=22n=4n，

由于bn=log4a2n+1，n=1，2， …，

∴bn=log44n=n．

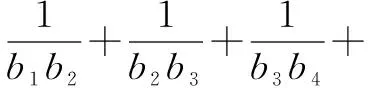
点评考查等比数列的通项公式及前n项和公式、裂项相消法求和，相关知识、方法的综合运用．

四、等差数列为根指数构造等比数列

例5 设an是首项为a1，公差为-2的等差数列，Sn为其前n项和，若S1,S2,S4成等比数列，且bn=2an，求bn的前n项和Tn.

分析数列an为等差数列，分析可知bn=2an为等比数列，然后求和.

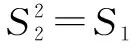
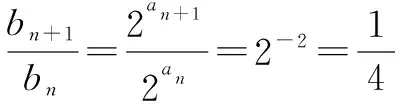
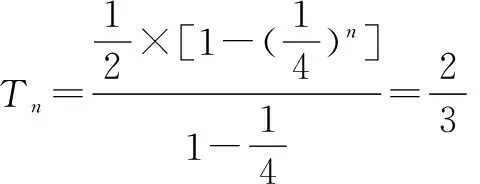
点评考查等差数列的通项公式、前n项和公式，等比数列前n项和公式，数列知识综合运用.

五、“等差×等比”型数列

例6 已知数列an满足：a1=1,nan+1-2an=2an,n∈N*.

分析(1)由定义法可证；(2)计算得出数列bn的通项公式，然后求和.

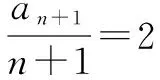
∴Sn=-2·20+1·21+4·22+…+3n-8·2n-2+3n-5·2n-1，

2Sn=-2·21+1·22+4·23+…+3n-8·2n-1+3n-5·2n，

∴-Sn=-2+321+22+…+2n-1-3n-5·2n

=-8+8-3n·2n

∴Sn=3n-8·2n+8.

点评“等差×等比”型的数列用错位相减法求和，为高频考点.

六、“等差÷等比”型数列

例7 已知{an}是递增的等差数列，a2，a4是方程x2-5x+6=0的根.

(1)求{an}的通项公式；

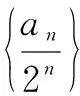
解(1)方程x2-5x+6=0的两根为2，3，由题意得a2=2，a4=3.

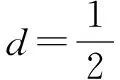
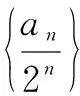
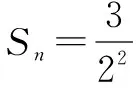
点评“等差÷等比”型数列采用错位相减法求和，为高频考点.

七、数列与函数融合

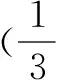
分析保证n≤6和n>6时数列单调递减，同时要a6>a7.

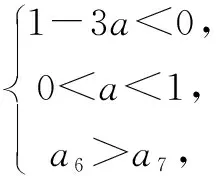
评注考察等差、等比数列的单调性，与函数的知识结合.

综上所述，等差、等比数列交汇题目以基本量的计算和定义的考查为主，对运算能力要求较高.备考时需要注重基本方法的积累，并提升运算素养.