易被忽略的余弦定理

温和群

(河北省沧州市第一中学 061001)

我们利用正弦定理、余弦定理研究解三角形问题时，有时会遇到解不出的尴尬，总觉得条件不够，无法将问题解决，其实往往是由于我们在解决问题时忽略了三角形中隐含的边角关系.如果注重了这个隐含关系后，能将问题顺利求解.

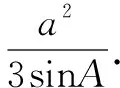
(1)求sinBsinC；

(2)若6cosBcosC=1,a=3，求△ABC的周长.

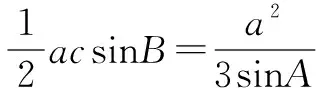
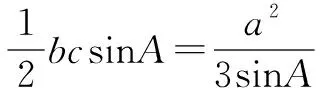
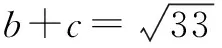
反思：我们在研究解三角形问题时，如果已知一个角或者求解出了一个角，一定不要忘了利用余弦定理可以导出三角形三边之间的一个等量关系，再结合题目其它条件将问题解决.

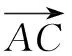
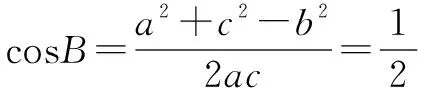
例3 在△ABC中，内角A,B,C所对的边为a,b,c，若a=3bcosC，

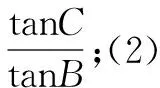
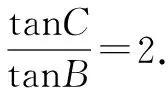
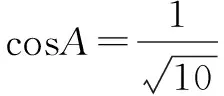
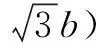
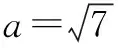
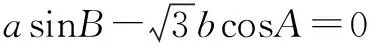
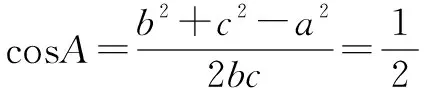
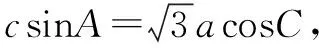
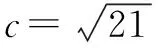
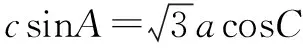
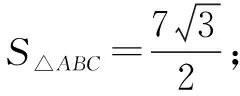
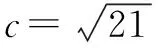
例6 在△ABC中，内角A,B,C所对的边为a,b,c，若a=bcosC+csinB,

(1)求B；(2)若b=2，求S△ABC的最大值.

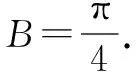
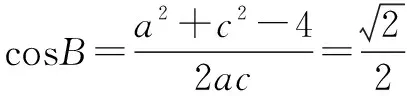
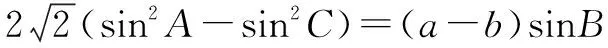
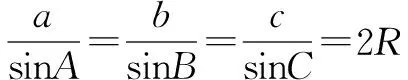
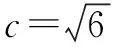
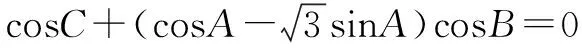
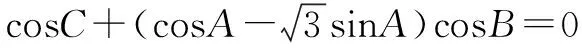
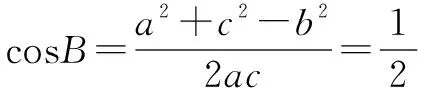
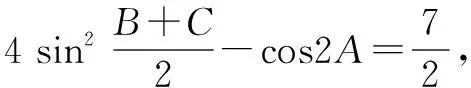
(1)求A；(2)若BC边上的高为1，求S△ABC的最小值.

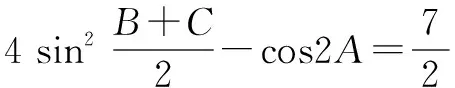
这个问题给了我们很大的启发，当解决一个问题遇到困难时，要更多地关注这一类问题的特点：这类问题有几个条件？结论是什么？用到怎样的方法解决的？考虑这些问题往往使得提高效率、事半功倍!