关于高中数学变形类试题的教学研究

王佳美

(北京市北京龙文教育 100096)

据实来说，高中数学就是以高考为圆心的数学教学.纵观近年的高考题目，题型越来越新颖，技巧性也越来越强，而变形技巧是其中较为常见的.熟练掌握变形解题技巧，可让解题过程变得更加的理性，让做题的效率更高.这对于即将面临高考的学生来讲，可以大大地增强学生们学好数学的信心，提高对数学学科的学习兴趣.教育的目的是培养学生独立思考和独立解决问题的能力，这是时代的要求，更是一个人终生学习的要求.变形试题的技巧性学习在学生的思维能力培养方面起到了非常重要的作用.

一、通过对变形技巧的学习，提高学习兴趣

对于大部分高中生来说，他们比较善于解答标准类型的题目.因为这类题目考查的是学生们基础知识的掌握程度，也就是我们平常所说的“死题”，按照原有的公式、概念一一代入就可以完成任务.但从长远看，这样的题目做得再多，也无益于提高学生的综合能力.所以，我们在进行数学题目的讲解教学时，为了有效地提高学生的解题技巧和反应速度，都会增加一些变形题.变形题就是在标准题型的命题基础上进行拓展和延伸，将知识点进行有效的隐藏或转化，让学生们在解题过程中不能一眼就看出用哪个公式或适用于哪条定理.要求学生对题目的整体意义和基础知识有较高水平的把握，在一定基础理论的指引之下对题目进行有计划、有目的的总结，然后进行合理的转化，在不改变原来命题考核意义的同时，让问题得到更简便的解决方法.

例如：学习了韦达定理之后，为了考查学生对这个定理的理解和应用能力，我设计了对应的练习题，其中有一个题目是这样的：

已知a，b是方程x2-x-1=0的根，求a4+3b的值.若要求出a、b的值按常规方法是很复杂的，在推导的过程中也容易在不同的环节出现错误.这时我们就可以通过变形的技巧解答，打破常规的先从已知条件开始解题的思路，先从结论出发，过程如下：

解因为a是方程x2-x-1=0的根，那么，a2-a-1=0,a2=a+1.

则a4=(a+1)2=a2+2a+1=a+1+2a+1=3a+2.

因此，a4+3b=3a+2+3b=3(a+b)+2.又∵a,b是方程x2-x-1=0的两个根,∴a+b=1,∴a4+3b=5.

二、通过变形技巧的学习，提高学生的逻辑思维能力

高中阶段的三角函数部分，无论在占比上还是难度上都是一个大角色，在一些求值、 化简、 证明以及解三角方程甚至是解几何问题等方面都有广泛的应用.在高中数学中它都算得上解题工具.但是由于三角函数部分公式众多，应用于实际解题中方法是多种多样的，简单的记忆和公式的套用在解决问题的过程中会让知识的应用显得捉襟见肘.如果学生们能熟练掌握三角恒等变换的技巧，就相当于变相地进行公式的记忆，同时还能对各内容之间的联系加深理解，促进逻辑思维能力的发展.

例如：已知θ同时满足asec2θ-bcosθ=2a和bcos2θ-asecθ=2b,且a、b均为不0，求a、b的关系.

显然有：cosθ≠0.

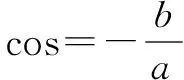
评析这道例题是“化弦”方法的一个具体的运用，在含同角的三角函数式的问题中利用的是切割弦之间的基本关系式，这些关系式在学生的大脑中一般是独立存在的，他们更善于对于问题的各个击破.在本题中，通过“正余互化”、“切割化弦”等方法减少了函数的种类，也就是变换了函数的名称，是函数实质的统一思想.这样有利于找到解决问题的途径.这样的变形技巧，要求学生必须对高中数学中相关的基础知识都心中有数，将各知识点进行有效的衔接和融合，长期有目的的练习会让学生的逻辑思维能力得到有效的提高.

三、通过学习变形技巧，培养学生良好的学习习惯

现在的高中生解决问题有很多的途径.在信息化的今天，要想获得一个问题的答案有很多途径，好多学生已经习惯了依赖各种辅助工具学习，这实际是一个非常不好的现象.在对变形技巧研究的过程中，我发现这是一个很好的让学生主动学习的方法.因为，变形类试题的解题思路是多角度、放射性的，它没有一个固定的模式可以遵循，这就给了学生们很广阔的想象和实践空间.在这个空间里，学生可以自由的发挥，达成自己的目标.这个过程要靠学生自己独立的思维，别人的建议只起辅助作用，长此他们会形成良好的自主学习习惯.

通过以上几点的介绍，主要是为了展示变形技巧在实际教学中的应用效果.对于解答问题来说这它是一种方法，而对于一个学生长远的发展来说它更是一种能力.即是能力就需在实践中不断的改进和创新，这样才能达到一个更好的灵活运用和综合提高的效果.