均值不等式和柯西不等式携手同行探求多元最值

武增明

(云南省玉溪第一中学 653100)

均值不等式和柯西不等式是两个著名的不等式，它们在解决有关数学问题的过程中，各自发挥了重要的作用.但是，对一些多元函数最值问题，特别是一些比较复杂的多元函数的最值问题，如果想到使它俩能够携手同行应对，便可发挥更大的威力.本文举例说明，如何让均值不等式与柯西不等式携手同行探求多元函数的最值问题时产生更大的效果.

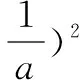
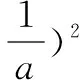
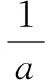
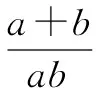
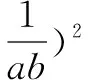
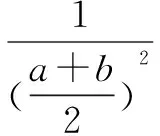
=(1+4)2=25，

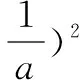
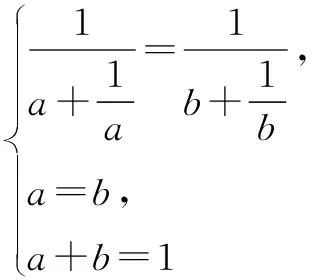
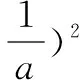
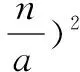
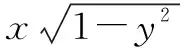
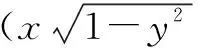
①≤(x2+y2)[(1-y2)+(1-x2)](运用二维柯西不等式)

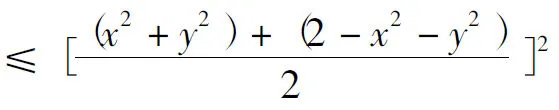
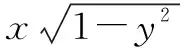
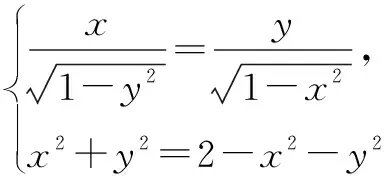
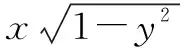
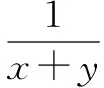
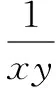
由均值不等式，得

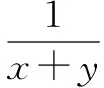
当且仅当x=y=z时，上式等号成立.

又由柯西不等式及①式，得

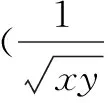
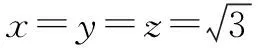
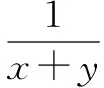
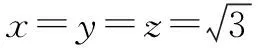
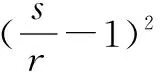
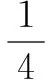
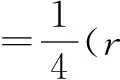
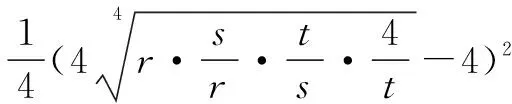
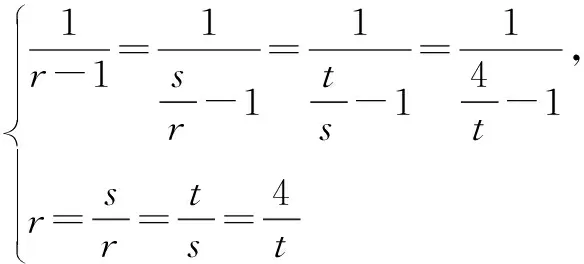
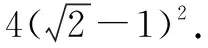
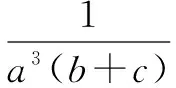
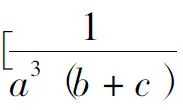
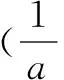
=(ab+bc+ac)2，

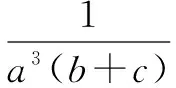
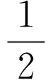
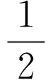
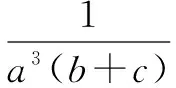
当且仅当a=b=c=1时，①处，②处的等号同时成立.

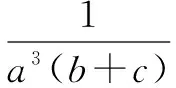
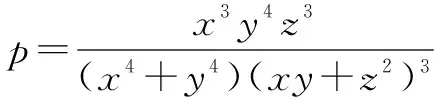
解注意到，x4+y4≥x3y+xy3=xy(x2+y2)，由均值不等式，得

(x4+y4)(xy+z2)3≥xy(x2+y2)(xy+z2)2(xy+z2)≥xy(x2+y2)·4xyz2·(xy+z2)=4x2y2z2·(x3y+xy3+y2z2+z2x2)≥4x2y2z2(2x2y2+y2z2+z2x2).

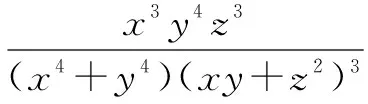
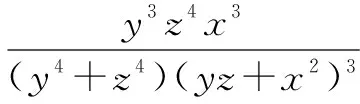
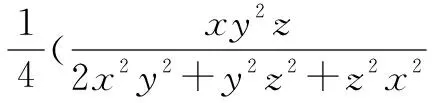
令a=xy，b=yz，c=zx，a>0，b>0，c>0，则

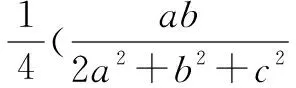
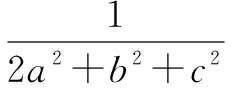
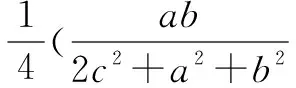
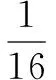
当且仅当a=b=c，即x=y=z时，以上各式等号均成立.

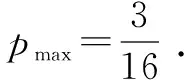
评注以上解答除了多次用到均值不等式和柯西不等式外，还应用了排序不等式，因此，这是一道高难度的竞赛题.

最后，特别强调，让均值不等式和柯西不等式携手共同探求多元函数的最值时，一定要关注等号是否会同时成立.