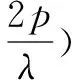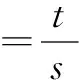一类圆锥曲线中直线过定点问题的探究与发现

喻秋生

(广东省深圳实验学校高中部 518055)

一、问题的提出

2017年高考全国卷Ⅰ理科第20题是一道关于椭圆中直线过定点的问题，题目如下：

(1)求C的方程；

(2)设直线l不经过P2点且与C相交于A，B两点．若直线P2A与直线P2B的斜率的和为-1，证明：l过定点．

在这道高考试题中，我们知道点P2是该椭圆的上顶点，kP2A+kP2B的值为常数-1，如果给出的点P2是平面内任意点，并且kP2A+kP2B的值为任意实数λ，结论又怎样呢？因此，我们提出更一般性的问题：

二、问题的探究

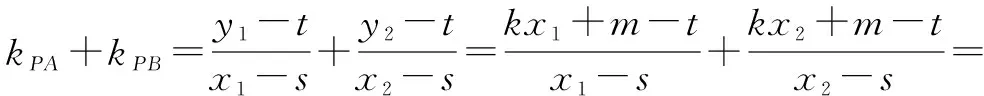
下面我们分λ=0和λ≠0两种情况进行探究．

1.λ=0，直线l过定点的情况

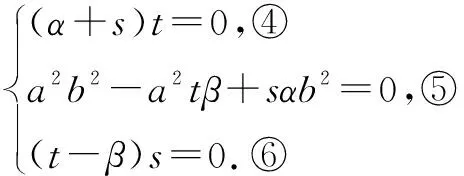
当s=0，t=0时，⑤不成立，即直线l不可能过定点；

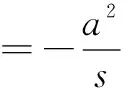
当s≠0，t≠0时，由④、⑥，得α=-s，β=t，则m=-sk+t，直线l的方程为y=k(x-s)+t，直线l过点P(s,t)与条件矛盾，此时直线l不过定点．因此，我们得出：

2. λ≠0，直线l过定点的情况

(1)点P在坐标轴上情况

由⑦得α=-s，代入⑧化简，得s=±a．

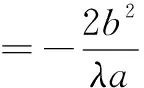
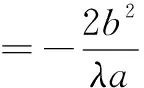
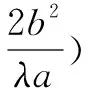
类似可得出点P在y轴上的情况，因此，我们得出：

点P的坐标直线l过定点的坐标(a,0)(a,-2b2λa)(-a,0)(-a,2b2λa)(0,b)(-2bλ,-b)(0,-b)(2bλ,b)

(2)点P不在坐标轴上情况

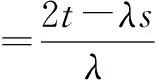
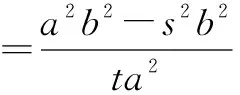
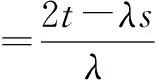
如果点P在C上时，则a2t2+b2s2-a2b2=0，等式⑩、⑩′均成立，即等式③对任意实数λ恒成立．

如果点P(s,t)不在椭圆上，则a2t2+b2s2-a2b2≠0，要使等式③成立，即要使等式⑩或⑩′成立，必须有λa2-λs2+2st=0，即(s2-a2)λ=2st．

当直线l的斜率不存在时，以上讨论结论也成立．因此，我们得出：

三、问题的推广

前面我们对椭圆中这类直线过定点问题进行了探究，用同样的方法对双曲线、抛物线进行探究，可以得出类似的结论(探究过程略)．

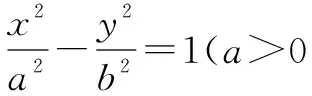
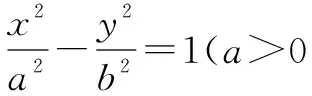
(1)若点P在坐标轴上，则当且仅当点P为C的顶点时，直线l恒过定点，并且点P的坐标与直线l过定点的坐标有以下关系：

点P的坐标直线l过定点的坐标(a,0)(a,2b2λa)(-a,0)(-a,-2b2λa)

结论6 已知抛物线C:y2=2px(p>0)，点P(s,t)，如果不经过点P且不与坐标轴平行的直线l与抛物线C相交于A、B两点，且直线PA与直线PB斜率的和为0，则当且仅当t=0，s≠0时，直线l过定点(-s,0)．

结论7 已知抛物线C:y2=2px(p>0)，点P(s,t)，如果直线l不经过点P且与C相交于A、B两点，直线PA与直线PB的斜率的和为λ(λ≠0)．