圆与轨迹的一组结论

张至君

(山东省淄博市实验中学高二1班 255086)

1.若一个圆C1内含于另一个圆C2，则与大圆内切与小圆外切的圆的圆心的轨迹为一椭圆，两圆的圆心为焦点，其长轴长为两圆半径之和；

2.在一个圆内有一点，则过该点且与已知圆相切的圆的圆心的轨迹为一椭圆，且其长轴长为已知圆的半径.

3.将圆的横坐标(或纵坐标)拉伸或缩短为原来的m倍，该圆变成椭圆；

4.连接圆内一定点与圆上任一点的线段的垂直平分线与圆上该点到圆心的连线的交点的轨迹为一椭圆.方椭圆的长半轴与圆的半径长相等；

5.两个同心圆较大圆上任一点与圆心的连线与小圆交于一点，从大圆上该点作x轴的垂线， 则过小圆交点向该垂线作垂线，其垂足的点的轨迹为椭圆.

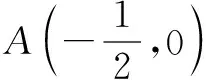
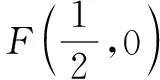
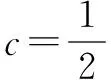
点评由已知点A与圆心F的对称性，可以猜测是椭圆或双曲线的两焦点，同时奠定了利用定义求轨迹方程的基础．

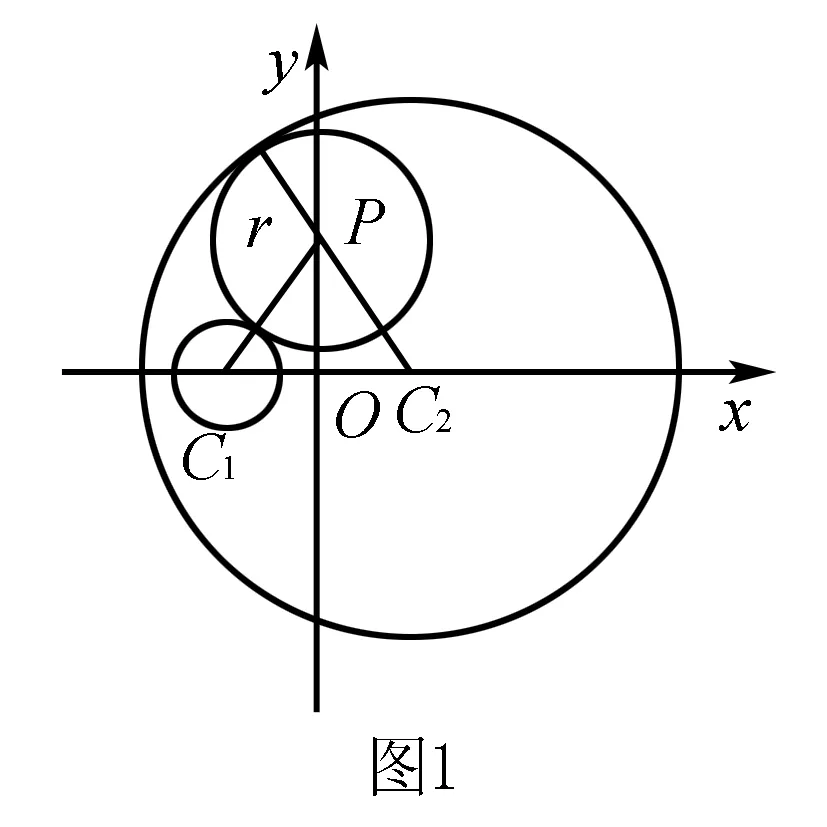
例2 已知两圆C1:(x+4)2+y2=9，C2:(x-4)2+y2=169，动圆P与C1外切，与C2内切，求圆心P的轨迹．

分析如图，由平面几何知识知，两圆相切时常连结两圆心，可利用切点在连心线上及圆心距与两半径的关系为突破口，求解此类题．

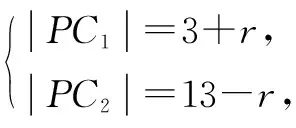
又16>C1C2=8，所以P点的轨迹是椭圆．

点评利用圆锥曲线的定义解题，是解决轨迹问题的基本方法之一．此题先根据平面几何知识，列出外切的条件，内切的条件，可发现利用动圆的半径过渡，恰好符合椭圆的定义．从而转化问题形式，抓住本质，充分利用椭圆的定义是解题的关键．

例3 已知点A1,0、B4,0，动点P满足PB=2PA，设动点P的轨迹为曲线C，将曲线C上所有点的纵坐标变为原来的一半，横坐标不变，得到曲线E.

(1)求曲线E的方程；

(2)A,B是曲线E上两点，且AB=2，O为坐标原点，求△AOB面积的最大值.

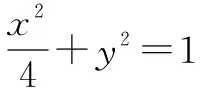
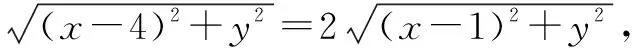
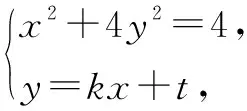
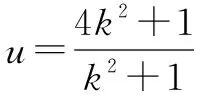
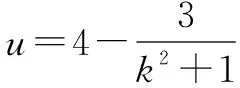
当斜率不存在时，△AOB不存在，

综上所述，可得△AOB面积的最大值为1.

点评对于最值问题，一般是利用函数思想，建立所求量的目标函数，转化为函数最值问题．要特别注意定义域．