“给值求角”问题解法探讨

曾宇嘉

(河北省任丘市第一中学 062550)

解决“给值求角”问题分两步：第一步，求该角的某种三角函数值；第二步，解三角方程，根据角的范围确定角的大小．

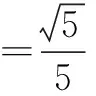
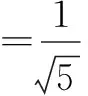
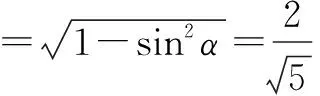
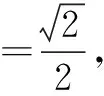
而α,β都是锐角，0<α+β<π,

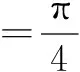
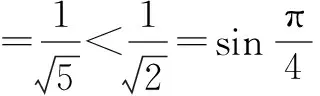
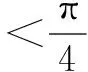
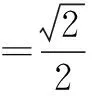
说明除了根据不等式的性质确定角的范围外，有时候要根据三角函数值的正负号进一步地缩小角的范围，有时候还根据三角函数值的大小进一步地缩小角的范围．

其实，0<α+β<π，本题中可以求α+β的余弦或正切更简单．

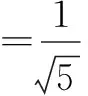
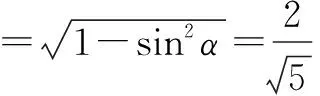
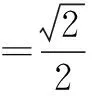
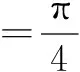
由此看来解决“给值求角”问题要注意两步之间的关系，如果求的三角函数不适当，就会给第二步确定角的范围带来很大的麻烦．

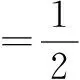
分析思路一，α=(α-β)+β，2α-β=(α-β)+α，用和角公式Tα+β先求tanα，再求tan(2α-β)；思路二，2α-β=2(α-β)+β，所以先用倍角公式T2α求tan2(α-β)，再用和角公式Tα+β求tan(2α-β)．

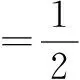
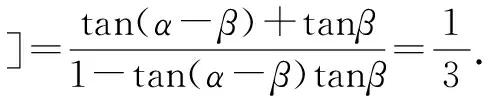
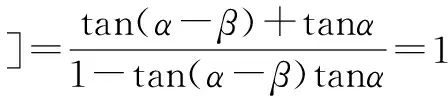
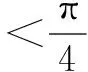
而tan(2α-β)=1,

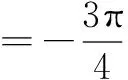
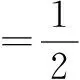
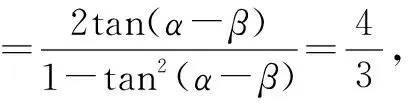
tan(2α-β)=tan[2(α-β)+β]

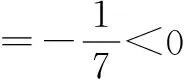
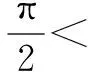
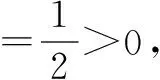
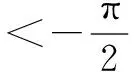
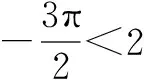
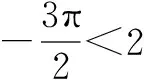
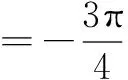
有时“给值求角”问题就象例2的思路二一样让人头痛，解决“给值求角”问题分两步：第一步，求该角的某种三角函数值；第二步，解三角方程，根据角的范围确定角的大小．需要注意：1.求该角的某种“适当的”三角函数值，“适当的”三角函数值可以帮我们缩小角的范围；2.求该角的某种三角函数值，要选择适当的角的变换与组合，原则是有利于缩小角的范围；3.缩小角的范围，除了根据不等式的性质确定角的范围外，有时候要根据三角函数值的正负号进一步地缩小角的范围，有时候还根据三角函数值的大小进一步地缩小角的范围．为了确定角的范围，我们宁可多求一些三角函数值，如果只利用不等式的性质确定角的范围，过程越多，范围越大，问题越多．