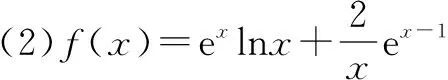构造函数 曲径通幽
2018-11-29吴嘉琛
数理化解题研究 2018年31期
吴嘉琛
(河北省张家口市第一中学 075000)
函数与不等式有着密不可分的联系,在不等式问题中,应重视以函数为桥梁,根据问题建立函数模型,用函数思想分析,解决问题.解(证)不等式问题,从实质上说,是研究相应函数的零点,正负值问题.所以,用函数与方程思想来处理这类问题,不仅会优化解题过程,而且会使我们迅速获得解题的途径.
一、参数的取值范围问题
在解决不等式恒成立问题时,一种重要的方法就是构造适当的函数,利用函数的图象和性质解决问题.同时要注意在一个含多个变量的数学问题中,需要确定合适的变量和参数,从而揭示函数关系,使问题更明朗化.现举例说明如下:
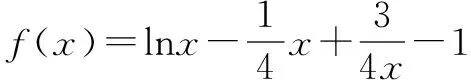
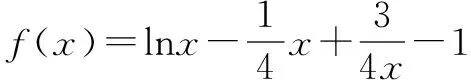
令f′(x)>0,可得1 令f′(x)<0,可得0 所以函数f(x)的单调递增区间是(1,3),单调递减区间是(0,1)和(3,+∞). 对于函数g(x)=-x2+2bx-4,x∈[1,2], 当b<1时,[g(x)]max=g(1)=2b-5; 当1≤b≤2时,[g(x)]max=g(b)=b2-4; 当b>2时,[g(x)]max=g(2)=4b-8. 综合所述,b的取值范围是(-, 在证明不等式时,当所证式子的结构非常复杂,用通常的比较法、配方法、分解因式等方法不能正常解决时,可以构造函数,通过求导,利用函数的单调性、极值等生成不等关系,证明不等式,使解答过程峰回路转.现举例说明如下. (1)求a,b; (2)证明:f(x)>1. 解析(1)略.二、证明不等式