规划之路哪家强
2018-11-29王培杰
数理化解题研究 2018年31期
王培杰
(河南省商丘市第一高级中学 476000)
规划问题的求解,适时挖掘其中的几何意义尤为重要,但对一些规划问题使用几何意义往往难以奏效,问题来了,规划之路哪家强?针对此问题,下面给出规划问题求解之路.
一、走不等式之路
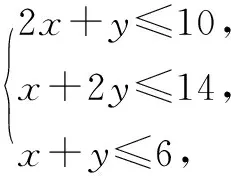


点评原约束条件只是一个线性规划区域,“xy”这个外衣包裹之下是不等式放缩问题,因此选择用基本不等式求解将会别有洞天.
二、走曲线之路
例2 同例1.
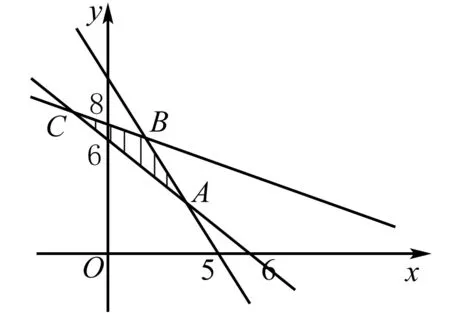


点评用曲线整体思考,既打通了xy与线性条件的思维障碍,又可避免分类讨论.
三、走分类讨论之路
例3 若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值是____.

解析原问题可以转化为如下的非线性规划问题:可行域为单位圆中的任意一点,直线y=2-2x将可行域分成两个部分,不妨将左下方的区域记作Ⅰ,将右上方的区域记作Ⅱ.
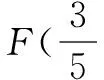
点评分类讨论体现了化整为零,各个击破的数学思想,使得整个问题的求解转化为各个简单问题的求解.
四、走换元之路
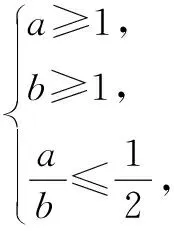


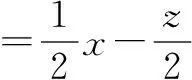
点评换元就是以新的变量替换旧变量,因此换元之路就是改变问题的呈现形式,在更为熟悉的背景之下解决问题.
上述规划问题的求解思路,体现了高考对能力立意的主旨,是对思维品质较好的体验之路,正所谓:
规划之路哪家强?化归求解道宽畅!
