一种考虑多种保障因素的作战任务间歇期战备完好率评估模型

高龙， 宋太亮， 曹军海， 邢彪， 闫旭

(1.陆军装甲兵学院 装备保障与再制造系， 北京 100072； 2.中国国防科技信息中心， 北京 100142；3.武警工程大学乌鲁木齐校区 装甲车技术系， 新疆 乌鲁木齐 830049)

0 引言

在以网络为中心的信息化联合作战背景下，武器装备体系之间的对抗贯穿于作战全过程，装备体系的战备完好性水平关乎着战争局势的最终走向。战备完好性水平是装备体系与保障体系等综合作用的结果，基于信息系统的体系作战中复杂的战场环境、激烈的对抗过程以及越来越短的作战任务持续时间，加大了在作战任务执行期进行使用保障与维修保障的难度，使得作战任务间隙期的装备保障作用越发突出。因此，作战任务间隙期的战备完好性评估对于优化保障体系结构、提高装备体系作战能力与保障体系效能具有重要意义。

战备完好性是指装备在平时和战时使用条件下，能随时开始执行预定任务的能力，其概率度量为战备完好率[1]。它反映了装备在特定时间节点出动参战的能力[2]，受到装备可靠性与维修性、保障体系结构与运行、部队训练等多种因素的影响，是衡量装备保障体系能力与效能的总体指标之一。文献[3-4]综述了战备完好性的定义、影响因素及典型评估模型；文献[5-6]采用仿真方法研究了单个装备的战备完好性；文献[7]在作战任务要求、任务通知时刻状态以及任务准备阶段维修保障方案确定情况下，给出了一种任务准备阶段复杂武器系统战备完好率评估模型；文献[8]提出了一种任务准备阶段给定机群状态条件下的机群战备完好率评估模型，建立了维修保障能力与机群战备完好率之间的关系；文献[9]提出了一种全面考虑维修保障和备件保障的新型战备完好率模型；文献[10]在考虑舰炮装备可靠性、维修性、保障性及维修过程情况下，建立了一种基于任务的战备完好性评估模型；文献[11]提出了一种基于Markov模型的机群完好率；文献[12]基于两站制和三站制的备件延误时间模型，提出了一种以现场可更换单元(LRU)的可靠性、维修性、保障性(RMS)参数表达的战备完好率模型；文献[13]分别给出了一个LRU故障、多个相同LRU故障以及多个不同LRU故障时的鱼雷贮存战备完好率模型；文献[14]结合导弹服役的实际保障情况，给出了基于扩散过程的导弹装备战备完好率评估方法和模型；文献[15]根据多层级可修复备件库存控制(METRIC)理论建立了备件的3级保障评估模型，并根据作战单元装备完好率提出了保障体系的体系保障度指标；文献[16]提出了一种基于任务驱动的机群战备完好性仿真模型，通过逻辑确定而工期随机的工程网络计划评审技术(PERT)网络和Monte Carlo方法获得了机群战备完好率随保障时间的变化曲线；文献[17]建立了一种适用于大型武器装备总体设计与研制阶段的战备完好性多层次协调优化分配模型。

总体来看，战备完好率评估涉及作战任务、装备本身及保障体系3个方面，由于研究重点和考虑问题角度的不同，先后出现了多种适用于不同情况的解析与仿真评估模型，但这些模型还有一些不足之处，主要表现在：1)目前研究多是针对导弹、鱼雷等单台装备和飞机、舰艇等单个装备群或作战单元，很少研究由多个装备群或作战单元组成的装备体系战备完好率评估问题，仅有文献[7]涉及此问题，但也只是针对使用同一套维修保障资源的复杂武器系统；2)现有评估模型比较注重维修保障工作，很少同时考虑弹药、油料、备件等消耗型资源的供应保障问题，仅有文献[9]提出的模型同时考虑了维修保障和备件保障，但该模型仅适用于单台装备或多台相同装备构成的装备群；3)现有模型多集中于作战任务执行期内的战备完好率评估，不适用于那些任务执行期间很难或根本不能进行保障的作战任务，只有文献[8]提出的模型适用，但要求每个故障装备中只能有一个故障的LRU；4)现有评估模型的建立方法都是基于LRU与车间可更换单元(SRU)这一基本的维修保障约定层次关系，但用该方法处理结构和行为更为复杂的装备体系与保障体系时会面临组合爆炸等问题。

因此，本文针对装备在执行作战任务期间很难或无法获得装备保障的实际情况以及现有评估模型存在的不足，在已知作战任务要求与装备体系结构与装备状态前提下，从装备体系保障需求出发，构建一种综合考虑保障体系中维修保障与供应保障等多种保障因素的作战任务间歇期战备完好率评估模型，最后通过一个实例来评估不同保障因素对战备完好率的影响以验证模型。

1 问题分析

作战任务间隙期的战备完好率评估与下一作战任务开始时刻、装备体系结构与作战任务通知时刻装备状态、保障体系中的多种保障因素等有关。在已知作战任务要求时建立评估模型，需要首先对装备体系与保障体系进行界定与分析。

从军队体制编制发展趋势来看，模块化与集成化是未来发展的主流，装备作战单元将是装备体系的主要组成部分。2011年《中国人民解放军军语》对作战单元的定义为：由同一层次的不同作战要素组成，能在一定范围内独立遂行作战任务的作战单位。因此，装备作战单元可指作战单元中的武器装备及其基本保障单元，其中基本保障单元是指由一定数量的保障人员及其配套的保障资源构成且具有一定保障能力的基本组合[18]，通常仅对归属的作战单元进行伴随保障，如对战斗单元进行保障的抢修分队、抢救分队、器材保障分队等。与装备作战单元相对应的是装备保障单元，它不隶属于某一作战单元，具有较高的保障能力，能同时对多个作战单元进行定点或划区保障，可遂行多种不同的保障任务，如保障旅、保障基地等。保障单元和基本保障单元一般在保障资源配置、维修保障与供应保障能力等方面有较大差异，研究中一般通过保障时间、完成保障需求的概率等对其进行反映。

为了便于评估装备体系中主战装备的战备完好性，本文约定装备作战单元所属基本保障单元为装备保障体系的一个组成部分，并以某一区域内的多个装备作战单元构建装备体系。含有多个不同装备作战单元的某战区装备体系及相应的保障体系交互关系如图1所示，其中基本保障单元和保障单元二者之间构成典型的两级保障体系。

如果装备作战单元在执行作战任务前没有保障需求，则可立即投入作战或使用；如果装备作战单元在执行作战任务前产生了装备保障需求，但其保障时间小于再次投入作战或使用所需的时间，则表明有足够的时间进行保障以投入下一次作战或使用。装备产生保障需求后，保障体系对其进行的保障过程如图2所示。当装备体系中的装备作战单元产生装备保障需求后，定位并评估该保障需求。如果基本保障单元有相应的保障资源且具备要求的保障能力，则在基本保障单元中完成保障任务；如果缺少相应的保障资源，则向保障单元申领；如果基本保障单元的能力不能满足该保障需求，则将此保障需求移送至可遂行多种保障任务的保障单元进行处理。与基本保障单元相比，保障单元一般具有较高的保障能力，可满足更为复杂的保障需求，且可多次重复使用的保障资源一方面送至本单元仓库作为贮备资源，另一方面补充基本保障单元。如果满足保障需求的资源为单次消耗型资源，则该保障需求涉及的资源退出保障体系；如果可多次重复使用的保障资源达到报废条件，则该资源退出保障体系。

综合上述分析可知，已知作战任务要求和装备体系时，对于任务执行期间很难或无法得到装备保障的情况，作战任务间歇期内装备保障体系中多种保障因素将对评估结果产生重要影响，主要包括保障需求的种类和数量、保障体系结构(由基本保障单元和保障单元构成的两级保障、保障单元数量等)、供应保障能力、维修保障能力以及保障资源满足率等因素，这些因素将是评估模型建立过程中需要重点考虑的。

从装备保障需求的角度来看，装备体系是保障需求的主要来源，其中各个装备作战单元在执行作战或训练任务时，会因遭受敌方火力打击、部件磨损、人为操作失误等因素而产生不同的装备保障需求。不同装备作战单元产生的不同装备保障需求可按照需求内容、所需保障单元与资源等因素的不同分解为多个不同的保障任务，例如某典型作战任务的保障需求可分解为使用保障任务、维修保障任务、供应保障任务。按照装备保障任务分解原则，可以将每一项保障任务进一步分解，并最终细化为元任务。元任务是装备保障任务空间中不能再进行分解的基本任务，全部元任务组成的集合构成元任务库。在保障任务空间中，每一任务项都存在其相应的元任务。装备体系保障需求-保障任务分解过程如图3所示。

因此，为了有效解决评估中面临的组合爆炸等问题，下面从装备保障需求出发建立战备完好率评估的数学模型。

2 评估模型建立

2.1 基本假设

为了突出研究重点、确保建模过程科学有效，本文模型做如下假设：

1) 作战任务通知时刻处于完好状态的装备在作战任务准备阶段不会产生装备保障需求；

2) 保障资源的供应保障速度基本固定，供应保障延误时间仅与路程有关；

3) 保障资源划分为消耗型资源和占用型资源2类，占用型保障资源总是处于空闲状态；

4) 保障资源申请处理时间服从正态分布；

5) 所有保障子任务的保障时间服从指数分布；

6) 作战任务间隙期内保障单元中的保障资源充足，能够满足保障需求的资源要求。

2.2 单个装备作战单元的战备完好率评估模型

2.2.1 保障资源获取概率

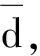
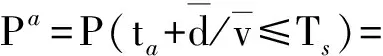
(1)

式中：Ts为任务间歇期时间长度；fa(ta)的函数形式可根据基层单位获取保障资源延误时间的构成来确定。

2.2.2 保障时间概率密度函数

设第l(1≤l≤L)类保障需求的保障时间为Tl，其处理过程分为R个阶段先后完成，即该保障需求被分解为R个串行的保障任务，第r(1≤r≤R)个保障阶段的处理时间Tlr服从参数为λlr的指数分布，在具备相应保障资源条件下该阶段能够成功处理该保障需求的概率为Plr，则保障需求分阶段处理过程如图4所示。

如果该保障需求直到最后1个阶段仍然没有被完成，则该需求的保障时间为所有保障阶段处理时间之和，其概率Pl为

(2)

(3)

由此可见，保障需求的处理过程服从库克斯分布[19]。库克斯分布包括了一族分布，其中任何分布的拉普拉斯变换(s)都是有理化的，可表示为

(s)=e-sxdfX(x)=

(4)

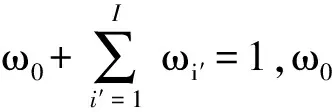
(5)

(6)

式中：t1为随机变量保障时间Tl的取值。

在此主要考虑由保障单元与基本保障单元二者构成的两级装备保障体系，保障需求的处理过程主要包括2个阶段，即基本保障单元处理阶段和上级保障单元处理阶段，对于上级保障单元无法处理的保障需求，可认为该需求的处理时间无限长，因此有R=3，Pl3=1，λl3=∞. 此时，第l类保障需求的保障时间的概率密度函数fl(t1)为

fl(t1)=Pl1λl1e-λl1t1+(1-Pl1)Pl2λl2e-λl2t1，

(7)

式中：Pl1和Pl2分别为基本保障单元和保障单元能够成功完成第l类保障需求的概率；λl1和λl2分别为基本保障单元和保障单元处理第l类保障需求时间的指数分布参数。

2.2.3 装备作战单元战备完好率

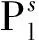
(8)

由此可得装备体系中单个装备作战单元在Ts时刻的战备完好率P(Ts)为

(9)

2.3 多个装备作战单元的战备完好率评估模型

在信息化联合作战背景下，执行作战任务的装备体系一般含有多个装备作战单元，各个单元相互协同以完成作战任务，在此过程中由可遂行多种保障任务的装备保障体系一同提供支持。因此，需要研究装备保障体系共享下多个装备作战单元的战备完好率评估模型。

设执行作战任务的装备体系包含M个装备作战单元，作战任务通知时刻有保障需求的作战单元数量为m(0≤m≤M)，包含L类保障需求。当m=1时，多个装备作战单元战备完好率评估模型与单个装备作战单元的评估模型相同。因此，本文重点研究作战任务通知时刻有m>1个装备作战单元有保障需求条件下，下一作战任务开始时的战备完好率。

2.3.1 保障需求相同的保障时间分布函数

作战任务通知时刻m个有保障需求的装备作战单元中有m1个是由于所属基本保障单元缺少相应的保障资源引起的，有m2(0≤m2≤m)个是由于所属基本保障单元的能力无法满足引起的，m=m1+m2，则m个需要保障的装备作战单元在作战任务开始时刻的战备完好率为：m1个需要保障的装备作战单元保障资源获取时间与m2个需要保障的装备作战单元保障需求保障时间均小于下一作战任务开始时刻Ts的概率。对于m1个有保障需求的装备作战单元保障资源获取时间小于Ts的概率Pa，可根据(1)式获得。对于m2>1个有保障需求的装备作战单元而言，存在保障需求相同与不相同两种情况。因此，下面首先分析m2个有保障需求的装备作战单元是由相同保障需求引起的情况。

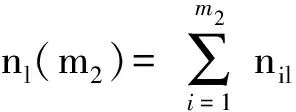
(10)

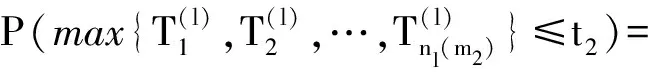
(11)

式中：(Fl(t2))nl(m2)表示分布函数Fl(t2)的nl(m2)次幂，Fl(t2)可根据(6)式或(7)式积分获得。

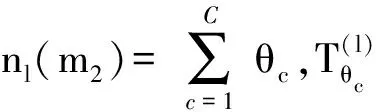
(12)

由于每个保障单元完成保障需求的过程是1个更新过程，则T(nl(m2),l)的分布函数Fm2,l(t2)为

(13)

2.3.2 保障需求不同的保障时间分布函数

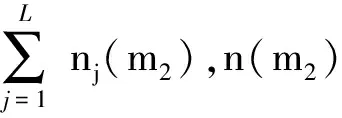
(14)

式中：T(nj(m2),j)为nj(m2)个第j类保障需求的保障时间，则T(n(m2),J)的分布函数Fm2,J(t3)为

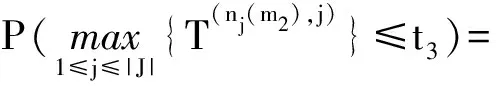
(15)

式中：t3为随机变量保障时间T(n(m2),J)的取值。当n(m2)≤C时，该分布函数可根据(11)式获得；当n(m2)>C时，该分布函数可根据(13)式获得。

2.3.3 多个装备作战单元的战备完好率

在给定下一作战任务开始时刻Ts条件下，根据T(nl(m2),l)和T(n(m2),J)的分布函数，可以得到在下一作战任务开始之前完成nl(m2)个第l类保障需求的概率为

(16)

则完成n(m2)个不同类型保障需求的概率为

(17)

综上所述可知，含有多个装备作战单元的装备体系在当前作战任务结束时有m个装备作战单元不是处在完好状态条件下，在下一作战任务开始时刻Ts可以恢复到完好状态的概率为

(18)

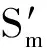
至此可得多个装备作战单元在Ts时刻的战备完好率Pe(Ts)为

(19)

式中：P0为当前作战任务结束时M个装备作战单元都处于完好状态的概率；Pm为当前作战任务结束时有m个装备作战单元有保障需求的概率。

装备体系通常可以遂行多种不同的作战任务，且这些作战任务通常都是多阶段的，对于具体的作战任务与任务阶段，可能只要求装备体系中的某些装备作战单元必须处于完好状态，此时只需要研究作战任务通知时刻与下一作战任务有关的有保障需求装备作战单元。

2.4 任务通知时刻装备体系状态求解

2.4.1 基本思想

分析(9)式与(19)式可知，装备体系战备完好性与作战任务通知时刻各装备作战单元所处状态有关，故需要进一步确定作战任务通知时刻各装备作战单元可能的状态及相应的概率P0,P1,…,PM. 通常可通过经验公式、一般Markov过程、排队网络模型及扩散过程获得[20]，但将这些方法用于装备体系中各装备作战单元状态确定时存在计算与求解复杂等问题。因此，本文针对装备体系中各装备作战单元及其保障需求的多态特性，给出一种基于向量通用函数的装备体系状态求解方法。

在现实世界中，部件或单元除了正常工作和完全失效两种状态外，还具有多种中间状态，即单元状态可有多种取值[21-23]。在执行作战任务过程中，装备作战单元可以产生多种不同类型的保障需求，每一种保障需求都可视为该装备作战单元的1个状态，同时在该装备作战单元中每一种类型的保障需求数量也可有多种可能的取值，故保障需求数量也是1个状态变量。因此，装备体系中各装备作战单元都可视为多状态单元，对其所处状态的分析与求解可转化为对多状态系统的分析[23]。通用生成函数是解决多态系统问题的常用方法，它能够明确地表达单元状态和对应概率与系统状态和对应概率的关系，并且可以通过简单运算由单元通用生成函数得到系统通用生成函数，具有计算速度快、适用范围广等特点[24-25]。

传统的通用生成函数都是针对离散随机变量的，其定义与运算见文献[26]，它要求部件状态和系统状态都只能有1个参数，但本文中装备体系装备作战单元具有多个状态参数(保障需求的类型与保障需求的数量)。因此，在利用通用生成函数分析装备体系状态时，需要对离散随机变量的通用生成函数进行改进以适应实际需要，故本文基于向量通用函数提出了一种新的分析与求解装备体系状态方法。

2.4.2 具体求解过程

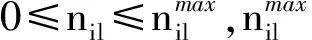
(20)

式中：z为多项式算子。

对于离散多态系统，部件状态gil和状态概率qil可以直接得到；对于多态退化系统，则需要对状态性能分布进行离散化，离散化时状态数可以根据需要来确定。

在装备体系中，装备作战单元i的保障需求由Li种不同类型需求组成，不同需求的发生基本独立，故Li种保障需求本质上是并列关系，则装备作战单元i的保障需求状态性能Xi可表示为

Xi=f(Gi1,Gi2,…,GiLi)，

(21)

式中：Gi1,Gi2,…,GiLi为装备作战单元i的第l(1≤l≤Li)类保障需求状态性能。(20)式同时也是一个并联结构函数，表示单元保障需求状态性能与不同类型保障需求状态性能之间的关系。根据(21)式，通过向量通用生成函数运算规则可得装备作战单元i的向量通用生成函数Ui(z)为

(22)

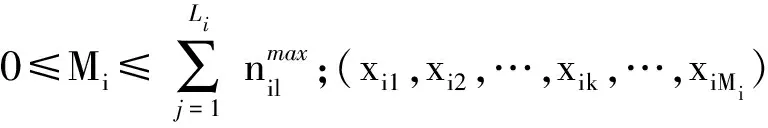
装备体系中各装备作战单元之间是一种弱耦合关系，各单元既可独立执行作战任务，也可彼此交互协同完成作战任务，但从保障需求出发分析装备体系状态时，可将各装备作战单元视为并联结构，则装备体系的状态性能Y可表示为

Y=f(X1,X2,…,XM)，

(23)

式中：X1,X2,…,XM为各装备作战单元状态性能。在得到各装备作战单元的向量通用函数后，通过向量通用生成函数运算规则可得装备体系的向量通用生成函数为

(24)

式中：Ms为装备体系状态数；{y1，y2，…，yk′，…，yMs}为作战任务通知时刻装备体系的状态性能；{q1，q2，…，qk′，…，qMs}为对应的状态概率。

至此，求得装备体系在作战任务通知时刻可能处于的状态及相应的概率，并且可对状态重新进行划分以便满足Ms=M，此时可将所得到结果代入(19)式，从而得到装备体系在下一作战任务开始时刻Ts的战备完好率。

3 实例分析

下面以某战区陆军装备体系为例，分析其对应的保障体系结构，基于本文提出的模型评估该装备体系在某次作战任务间歇期的战备完好率，并进一步定量分析供应保障速度、保障单元数量、维修保障能力等保障因素与装备体系战备完好率之间的关系。为了对比验证模型计算结果的合理性与准确性，通过Monte Carlo仿真方法对上述战区陆军装备体系的战备完好性进行评估，仿真过程建立在装备体系结构模型、保障体系结构模型、维修与供应保障模型及保障资源模型的基础上，仿真时钟采用面向时间间隔与面向事件相结合的时钟推进机制，以加快仿真执行速度。限于篇幅，具体仿真过程不再赘述，下面主要论述如何通过本文所提模型评估装备体系的战备完好率。

3.1 实例数据

根据作战部署，执行某次地面防御作战任务的装备体系由M=5个战区陆军合成旅所属装备构成，整体呈现出环形防御态势。每个合成旅下辖1个基本保障单元，具备一定的维修保障能力和供应保障能力。为满足执行作战任务的装备体系保障任务需求，在距离前沿一定位置的后方配置c=2个保障旅。保障旅的资源配置一般相对科学合理，具有较高的保障能力，能够遂行多种不同的保障任务。保障旅与合成作战旅所属基本保障单元之间构成两级保障体系结构。

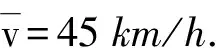
该装备体系在执行任务过程中，各个装备作战单元会产生多种类型的保障需求，每种保障需求数量又会有多种可能的取值，即每个装备作战单元保障需求类型和数量都是多态变量。假设任意装备作战单元i最多可能产生L=4种不同类型的保障需求，即有Li∈{1,2,3,4}；在任一装备作战单元中，不同类型保障需求的数量nil最大为8，即有nil∈{0,1,2,…,8}，且满足1≤l≤Li. 通过仿真方法获得装备作战单元在作战任务通知时刻状态性能gil对应的状态概率qil如表2所示，其中装备作战单元5为完好状态，没有保障需求。

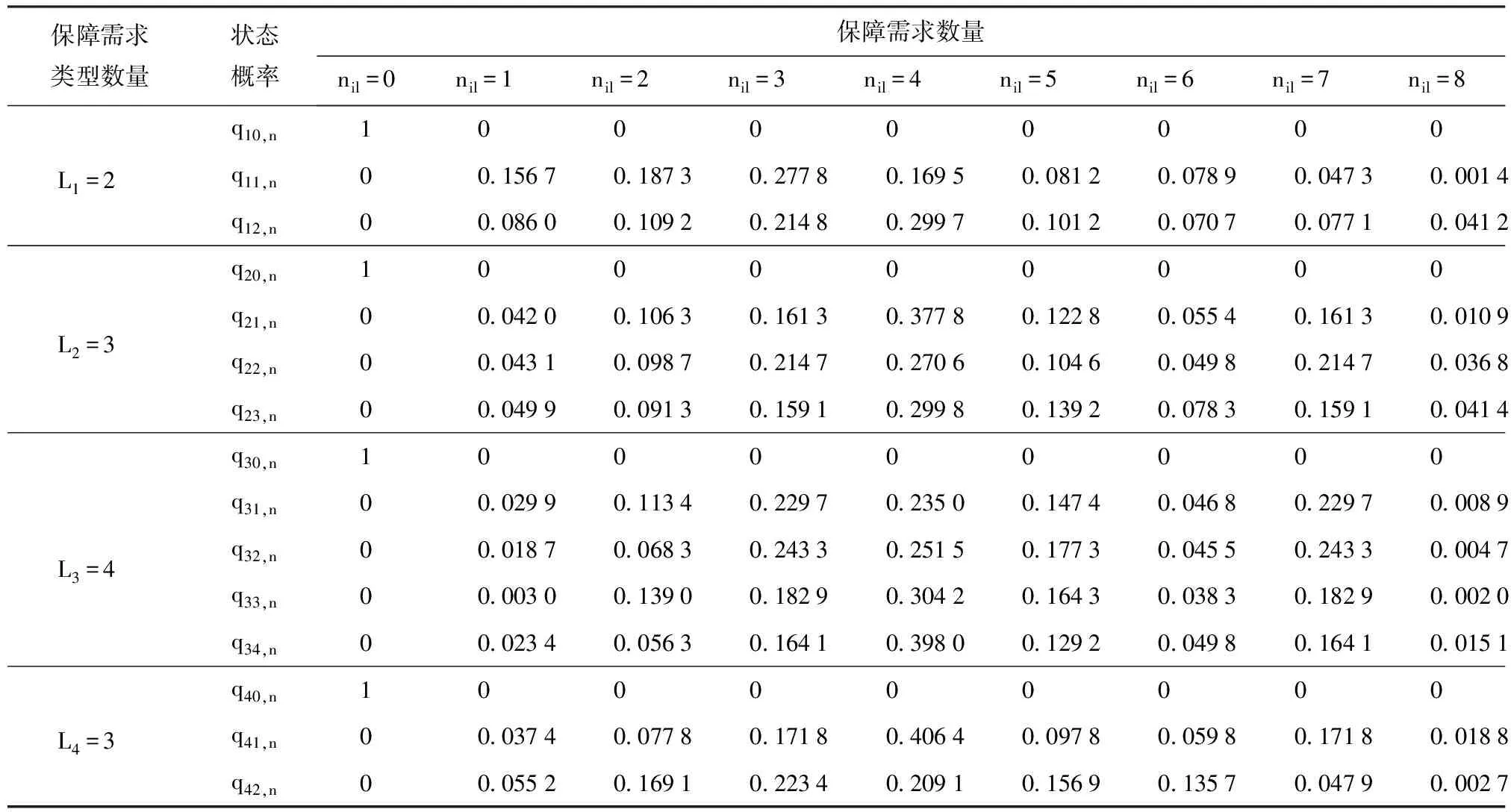
表2 任务通知时刻各装备作战单元的状态概率qil

3.2 状态求解

根据表2中提供的装备作战单元状态性能和状态概率数据，通过(20)式可以得到各个装备作战单元不同类型保障需求的向量通用函数。表3给出了装备作战单元1的3个向量通用函数，篇幅有限，其他单元的各个向量通用函数不一一列举。在得到装备作战单元1不同类型保障需求的Uil(z)后，根据(22)式可得装备作战单元1的向量通用生成函数为U1(z)，见(25)式，其他装备作战单元照此进行。

表3 装备作战单元1不同类型保障需求的Uil(z)

U1(z)=0.013 5×z2+0.016 1×z3+0.023 9×z4+…+0.000 1×z9+0.017 1×z3+…+0.001 9×z15+0.000 1×z16=0.013 5×z2+0.033 2×z3+0.078 1×z4+…+0.007 0×z14+0.002 0×z15+0.000 1×z16.

(25)

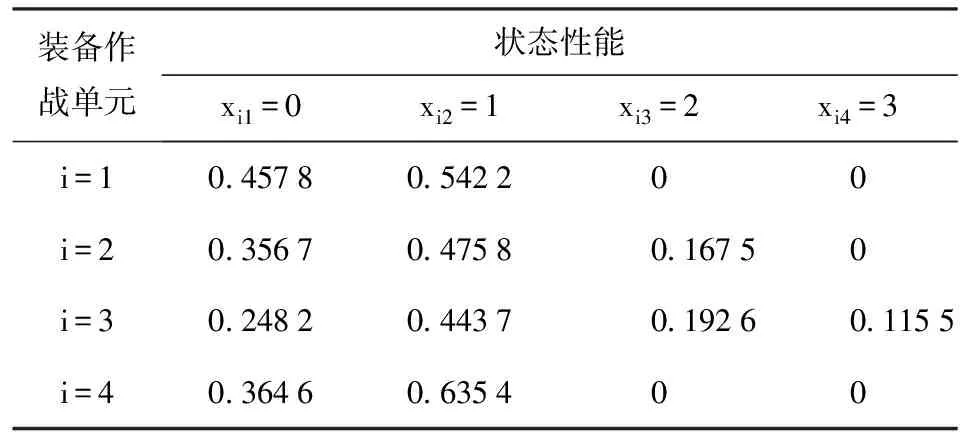
表4 状态重新划分后的状态概率

根据重新划分后的单元状态求得装备体系向量通用函数U(z)见(26)式。

U(z)=0.014 8×z0+0.037 2×z1+0.030 3×z2+0.008 2×z3+0.052 2×z1+0.131 4×z2+…+0.024 6×z6+0.006 7×z7=0.014 8×z0+0.089 4×z1+0.219 2×z2+0.286 8×z3+0.226 4×z4+0.117 3×z5+0.039 5×z6+0.006 7×z7.

(26)

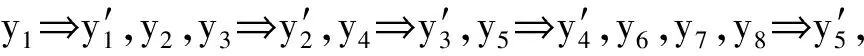
此时有P0=0.014 8，P1=0.308 6，P2=0.286 8，P3=0.226 4，P4=0.163 5.

至此，通过向量通用生成函数获得了装备体系在任务通知时刻处于完好状态及各种需保障状态的概率，将P0、P1、P2、P3和P4代入(19)式，可得到多个装备作战单元在下一作战任务开始时刻Ts的战备完好率。

3.3 评估分析

在作战任务准备阶段，所有保障需求的处理过程可分为2个阶段：当r=1时，该阶段保障需求处理时间Tl1(1≤l≤4)服从参数为λl1=3.5的指数分布；当r=2时，该阶段保障需求的处理时间Tl2服从参数为λl2=2.5的指数分布。对于1个保障需求，各个阶段能够处理该需求的概率分别为Pl1=0.8，Pl2=0.7. 同时，在作战任务通知时刻需保障的装备作战单元中，有1个单元是由于所属基本保障单元缺少相应的保障资源而产生保障需求，即有m1=1，m2=3. 为了使验证示例具有一般意义，假设m2个有保障需求的装备作战单元是由不同保障需求引起的，同时令θ1/θ2=1，则可通过(15)式计算出m2个有保障需求的装备作战单元保障时间分布函数Fm2,J(t)，进一步可求得装备体系在下一作战任务开始时刻战备完好率Pe(Ts).

图5为通过Monte Carlo仿真方法与通过本文所提模型求得装备体系在不同任务间隙期长度下的战备完好率。从图5中可以看出，两条曲线在整体趋势上基本保持一致，特别是在前期两条曲线基本吻合。由于Monte Carlo仿真结果受随机因素影响比较大，仿真结果曲线会有小幅波动。在两条曲线的后期，仿真结果曲线略小于模型结果曲线，这是因为仿真模型的占用型保障资源不是总处于空闲状态，从而引起一定的保障延误。但总体而言，本文提出战备完好率评估模型基本准确可信。下面主要分析供应保障速度、维修保障能力等保障因素对装备体系战备完好性的影响。

图6为3种不同保障资源平均供应速度对装备体系战备完好率的影响。从图6中可以看出，供应保障速度对战备完好率的影响比较显著，特别是在曲线的前期与中期，较高的供应保障速度可使战备完好率在短时间内达到1个较高值。但供应保障速度不是越高越好，从图上曲线的后期可知，60 km/h速度虽然使战备完好率较早地保持在1个较高的水平，但是与45 km/h速度时获得的结果相比并没有大幅度提升。

图7为保障需求处理过程中处理时间服从不同指数分布时通过评估模型得出的装备体系战备完好率。指数分布的参数λl1和λl2在本质上表征的是保障体系中维修保障的快慢，是维修保障能力的一个方面。分析图7中的曲线可知，2个参数在曲线的前期与中期对战备完好率有一定影响，但在后期几乎没有影响，这一趋势表明在一定的任务准备时间长度内，维修保障的快慢会对战备完好率产生一定影响。

图8为保障需求处理过程中每个阶段能够成功处理该需求的概率。参数Pl1和Pl2在本质上表征的也是保障体系中维修保障能力的大小。从图8中可知，概率越大获得的战备完好率越大，但参数越大对战备完好率的提高越不明显。

图9为保障单元数量分别为1、2和3个时求得的装备体系战备完好率，保障单元的具体部署分别见图10(a)与图10(b). 从图9中的曲线可知，保障单元的数量对战备完好率有显著影响，保障单元数量越多，战备完好率越高。但在实际中，受战场环境、保障费用等因素制约，保障单元不可能无限增加，此时需要权衡战备完好率的提高与保障费用的增加。

综合分析图5～图10可知，装备体系在作战任务间隙期的战备完好性水平受到保障体系结构、供应保障能力、维修保障能力以及保障资源等多种因素影响。为了提高装备体系的战备完好性，需要建立精简高效的保障体系结构，科学合理地配置保障资源，增强供应保障能力；在作战指挥与作战任务规划中，尽量延长装备作战单元的作战任务间歇期，并注意加强任务间隙期的保障能力。

4 结论

本文针对装备体系战备完好性评估问题，从装备保障需求角度出发，提出了一种新的综合考虑多种保障因素的作战任务间隙期战备完好率评估模型，并给出了一种基于向量通用生成函数的装备体系状态确定方法。通过实例分析可知，本文所提模型与方法能够获得装备体系战备完好率，并可定量确定多种保障因素对装备体系战备完好率的影响。本文所提战备完好率模型弥补了已有解析评估模型的不足，对于优化保障体系结构、提高装备作战能力与保障效能具有一定的参考价值。