浅谈整数十进制与N进制间的“砌权法”转换技巧
2018-11-28珠海市理工职业技术学校陈金坡
文/珠海市理工职业技术学校 陈金坡
在中职学校中,数制转换的学习和应用涉及到多个学科,比如:《数学》 《电子技术》 《单片机》《PLC》 《微机原理》等,对于即将成长为技能型人才与高素质劳动者的中职生来说,它具有重要的实践应用价值,同时也是一个学习难点。
一、问题的提出
数制即选取一定的进位规则,用多位数码来表示某个数的值,如表1所示。可用按权展开的数学通式来表达任意进制数:
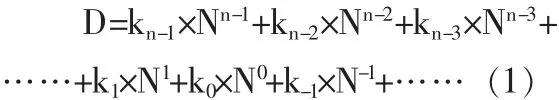
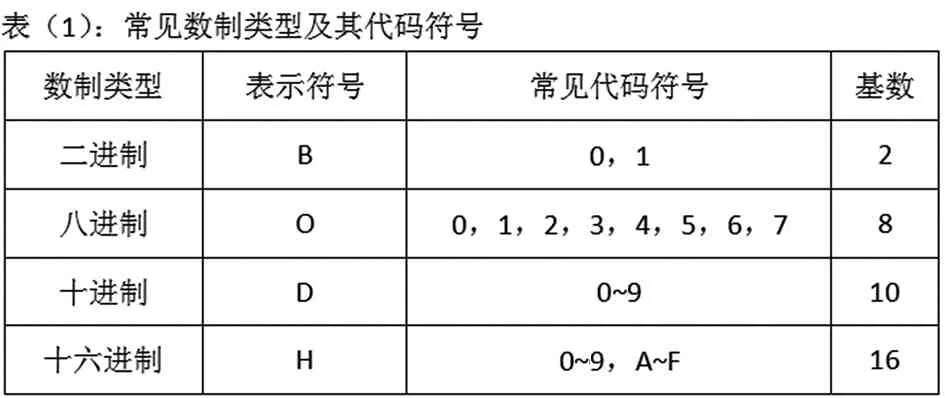
表1 常见数制类型及其代码符号
式 (1)中,D代表任意进制数,n为整数部分的总位数,kn-1为第n-1位数的数码,Nn-1为第n-1为的权,N代表某一进制。由于数制转换对中职生不作研究要求,基本实践应用中只有整数部分,所以本文对数制转换过程中的小数部分不作研究对象。
传统的数制转换方法,通常采用按权展开法、基数乘除法、比例法,如图1常见进制间转换方法所示。
基于进制位数的 “比例法”,适用于二进制与2n进制间的转换,其它进制间的转换由于位数不匹配而不适用,此方法较为简单、具体,学生容易掌握,在此不作累述。
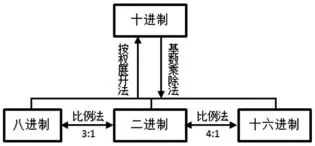
图1
基于基数的乘除法,适用于十进制转换为N进制,在整数转换部分,只需要用到除基取余法,即将需要转换的十进制数,连续除以转换目标进制的基数,直到商为0,再逆序排列余数可得到结果。
例题1.将十进制数19转化为二进制数。
解:根据除基取余法,将19连续除以二进制的基数2,取出余数,具体如下:

所以: (19)10=(k4k3k2k1k0)2=(10011)2
在实际教学中,我们发现学生对基数乘除法的掌握情况,达不到我们想要的教学效果。可能转换过程过于抽象,而除法取余是学生数学运算的硬伤,学生经常出现除法取余理解困难和答案高低位错乱的情况。
基于数学通式的按权展开法,适用于N进制转换为十进制,在整数转换部分,按照N进制的位权形式展开多项式和的形式,通过求幂、乘法、加分运算得到结果。
例题 2.将二进制 (101)2转化为十进制数。
解: (101)2=1×22+0×21+1×20=(5)10
在实践应用过程中我们发现:按权展开法公式过于复杂,学生难以记忆,书写容易出错;且与基数乘除法一样,在转换过程中具有单向性,学生容易混乱。
面对这样的问题,能否找到一种简单的方法,既可以不涉及到除基求余和求幂运算,又能够满足中职生的数制转换需求?笔者根据多年的教学经验,归纳出利用进制位权值凑数相加的 “砌权法”转换技巧,可以轻松进行整数十进制与N进制间的转换。
二、 “砌权法”的定义及适用范围
“砌”即拼凑, “权”是进制的位权, “砌权法”就是利用进制位权值固定的特点,将需要转换的进制列出若干位权,再根据位权和进制数之间的规律进行拼凑而成。具体过程可以分为三个步骤:
①列权:将相应进制数的若干位权列出,如下表2常见进制的位权表所示。
②定权:确定最高位权值;在十进制转换N进制过程中,假如需转换的十进制数为D,则取位权值小于D的最高位。在N进制转换十进制过程中,N进制数有几位则定位权几位。
③砌权:将各权值由高位向低位凑数相加完成转换。
我们可以发现,进制位权的规律是按照进制的n次方值列出,简单的理解就是,任意N进制的第1位位权都是 “1”,相邻高位位权为低位位权的N倍。由于 “砌权法”在带小数的数制转换过程中,并不具备优势,所以 “砌权法”只适合中职学生在整数十进制转任意进制实践应用过程中使用。
三、 “砌权法”的应用及优点
在十进制转换为N进制过程中,我们如何利用 “砌权法”避免除法运算,并且让过程简单、具体。我们选择较大的十进制数转换为难度较高的八进制数来验证。
例题3.将十进制数172转化为八进制数。
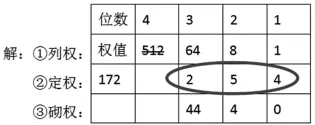
在第②步中,位权值小于172的最高位是3,可以忽略第4位位权值。在第③步中,第3位的权值为 64,3个64大于 172,所以选择2个64来拼凑,剩下44在第2位进行拼凑,可以选择5个8来拼凑,剩下4在第1位进行补充,可以得出答案为: (172)10= (254)8。
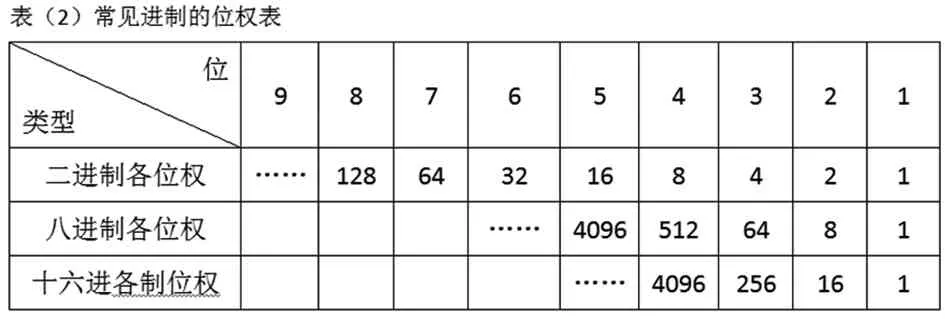
表2 常见进制的位权表
通过例子我们发现,利用 “砌权法”可以避免除基取余过程的抽象,又可以将解题过程模块化,简单易懂,有利于学生理解和掌握。
在N进制转换为十进制过程中,我们如何利用 “砌权法”简化按权展开法的复杂公式,避免书写错误。我们选择十六进制数转换为十进制数来验证。
例题4.将十六进制数2AF转化为十进制数。
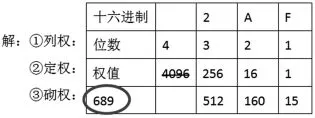
在第③步中,将十六进制的2AF分别乘以下面对于的权值,其中A代表10、F代表15,分别可得到 512、160、15,再将三个数相加可以得到答案:
(2AF)16= (689)10
通过例子我们发现,学生不必再背诵复杂的数学通式,不必再纠结求幂过程下标和上标的意义,可以步步为营的进行准确转换。
四、结论
本文基于中职学生数学运算能力及逻辑思维较为薄弱的现状,归纳出利用进制位权值凑数相加的“砌权法”转换方法,可替代整数十进制与N进制间转换的按权展开法和基数乘除法。因为 “砌权法”相对于按权展开法和基数乘除法具有以下优点:
a.过程直观,通过一个表格就可以详细解题;
b.步骤独立,每一个步骤都相对独立,容易掌握;
c.算法简单,免去除基取余法和求幂这个硬伤,实现双向转换。
