高考中三角函数内容考查研究①

陈 昂 任子朝 赵 轩

(教育部考试中心 100084)

1 三角函数的地位和作用

三角函数内容是高中数学中的基础内容、也是重要内容之一. 历年来在数学科高考中都占有重要地位. 张景中院士指出：“在中学数学课程中，三角函数的内容至关重要. 三角函数不仅是连接几何与代数的一座桥梁，还是沟通初等数学与高等数学的一条通道.”[1]三角函数除了具有一般函数的性质外，还呈现出与其他基本初等函数不一样的特征，例如具有其独特的周期性和对称性，并且与向量、复数、立体几何、解析几何等数学知识有较为紧密的联系. 更进一步，三角函数知识具有丰富的实际背景和广泛的应用价值，在其它学科中都有广泛的应用，例如地理学、力学、电磁学等. 正是因为三角函数内容具有这么丰富的特征，因此在高考中考查体现了基础性，综合性和应用性的特征.

2 三角函数在高考中的考查特点

根据《普通高等学校招生全国统一考试大纲的说明》对三角函数部分的要求，这部分的内容分为13个知识考点，对每个知识考点分别给出知识要求层次(以理科数学为例，见表1).

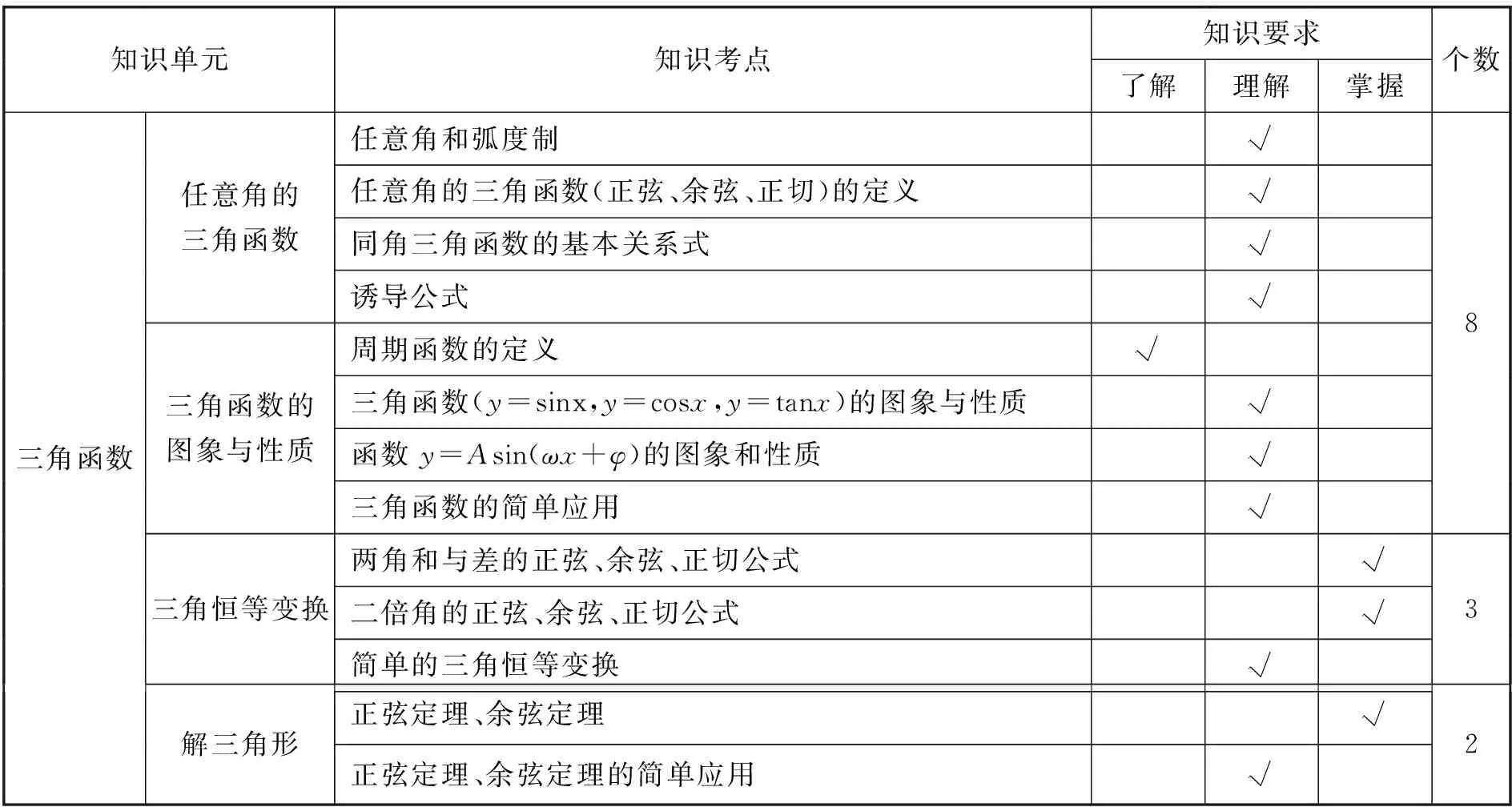
表1 数学(理科)知识考点及其考核要求

课程标准实施以来，高考对三角函数的考查呈现出新的特点. 一是因为近年来课标中新增内容比较多，三角部分内容总体的题量有所控制，在解答题中，与数列内容交替 ，一般是一大两小，难度控制中等，在不出解答题的年份，是三道小题，但难度没有下降，保持在中等难度. 二是对三角函数的考查突出基础，体现综合，对恒等变形的要求和过去比有所下降，更多强调对公式的灵活运用.

数学科高考对三角函数的考查主要体现在以下四个方面：1. 利用数形结合考查，通过图形分析、研究、总结三角函数的性质和图像特点；2. 利用三角公式考查，创设试题情境，灵活运用公式，解决问题；3．利用真实情境考查，考查解三角形内容，体现三角函数的工具性作用；4. 体现思维深度，考查创新意识.

2.1 利用数形结合考查

三角函数的基本特征之一就是具有很强的几何特点，这是与其他基本初等函数不一样的地方，高中课本中的三角函数是以单位圆的定义形式给出的. 利用图形解释、理解知识，能更好的帮助学生理解比较抽象的概念，形成直观印象. 因此，在对三角函数知识进行考查时，可以充分利用数形结合的思想命制试题.

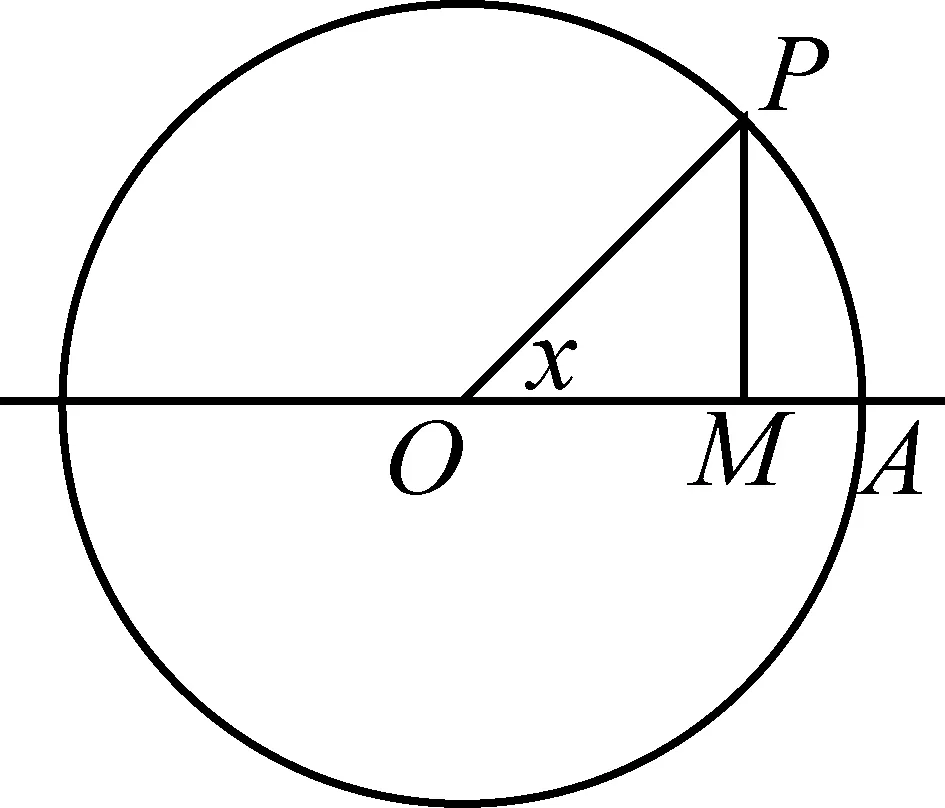
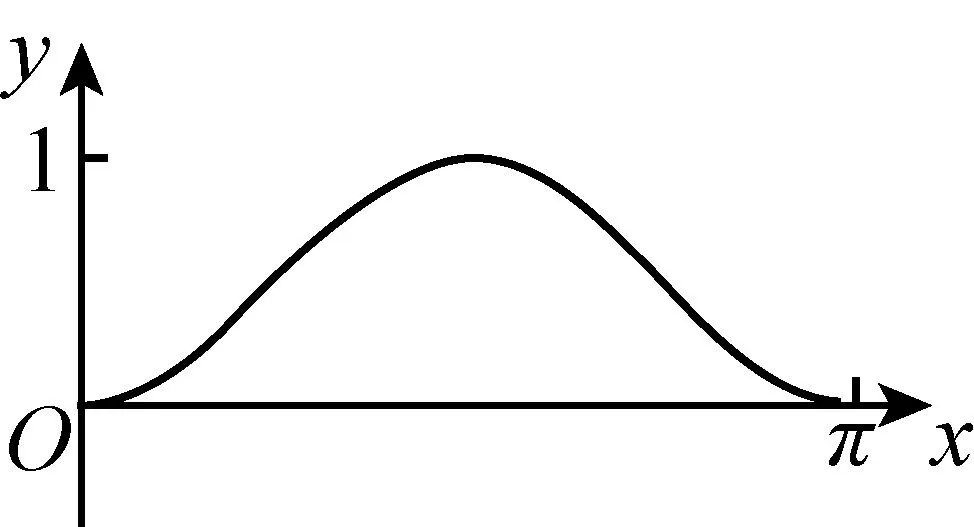
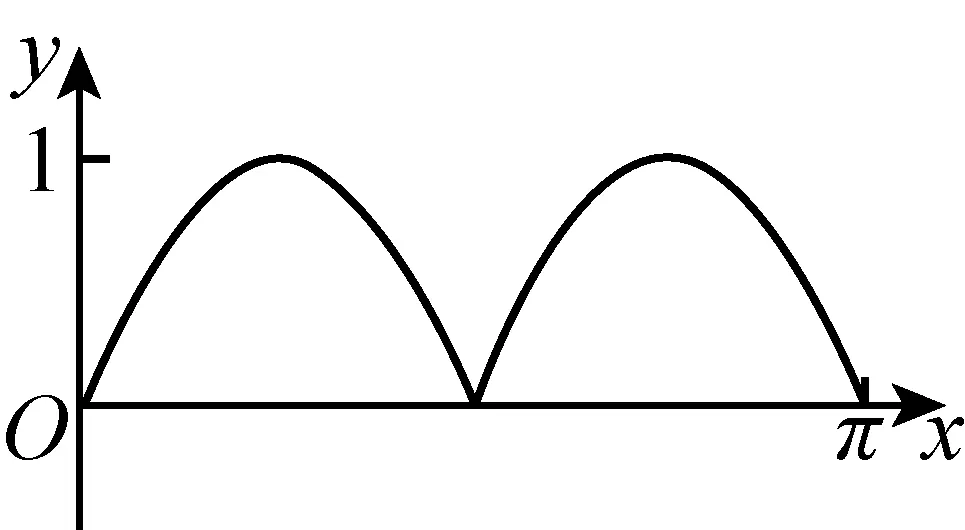
例1如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，过点P作直线OA的垂线，垂足为M. 将点M到直线OP的距离表示成x的函数f(x)，则y=f(x)在[0,π]的图像大致为( ).

A

B

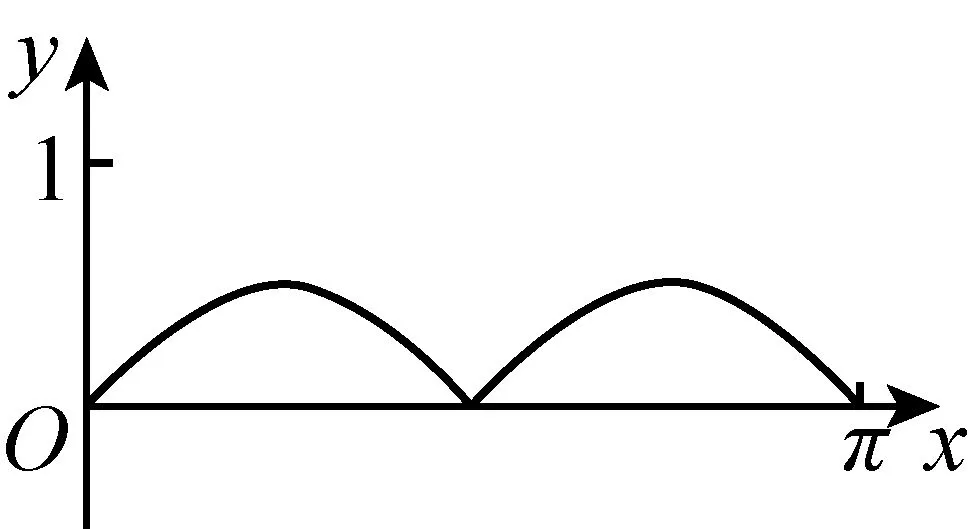
C

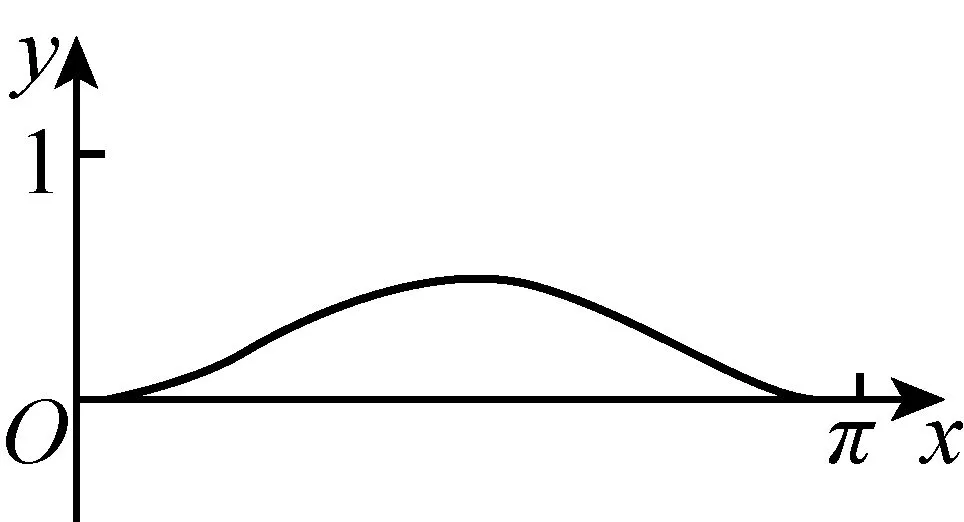
D

考生在初中的时候学习过锐角三角函数，而高中阶段的知识难度和抽象程度更大. 本题的背景正是借助单位圆给出了三角函数的自然语言表征与三角函数的图像表征，即“点M到直线OP的距离”与四个图像的选项. 考生要建立这两者的关联，考生可以选择以三角函数的解析式表征为桥梁，也可以选择三角函数的列表法表征(即寻找特殊值)定性地建立三角函数的自然语言表征与三角函数的图像表征之间的关联，解决问题.

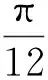
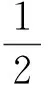
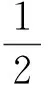
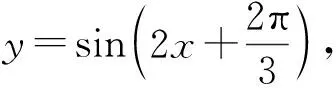
2.2 利用三角公式考查

与高中其他内容知识相比，三角函数知识的最大特点是公式. 通过对公式的应用，重点考查考生的逻辑推理能力和运算求解能力.在现行高中数学课程中，要求考生掌握的三角恒等变形公式主要有两角和与差的正弦、余弦及正切公式，正弦、余弦的二倍角公式等. 相对以前的考试大纲来说，考生要记忆和掌握的基本公式是减少了，所以更强调公式的灵活运用. 这些公式之间存在着密切的联系，公式之间可以相互转化，互相推导. 例如诱导公式中角的周期性变化、正负取值，两角和与差公式中角的组合变化等，因此在考查时，重点考查对一个公式的灵活运用即可.

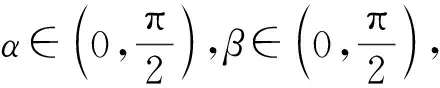
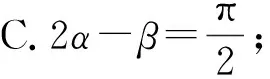
本题设计的一个思路是，将正切函数变形为容易研究的正弦函数与余弦函数的有关等式，考查考生对三角函数的诱导公式及三角恒等变形的有关知识与技能的掌握. 考查考生关于三角函数的运算求解能力. 由于等式含有两个变量α与β，因此必然存在一个变形，使得这个看起来是二元三角函数的关系转换为考生熟悉的一元三角函数关系. 此问题的关键设计是如何把二元关系转换为一元关系，三角恒等变形的基本公式(如两角和差公式，二倍角公式)就成为基本的设计素材.

例4已知sinα+cosβ=1，cosα+sinβ=0，则sin(α+β)= ．

2.3 利用真实情景考查

近年来，三角函数试题的背景越来越丰富，不少试题背景涉及实际生活情境，考查解三角形内容，体现了三角函数的工具性特点，考查了考生的应用能力. 这主要体现在拓宽试题材料来源，设计自然科学、社会科学和现实生活等多个领域中能运用三角函数知识的内容作为背景材料，考查考生运用数学知识分析、解决学习和生活中实际问题的能力，体现出三角函数的工具性作用.

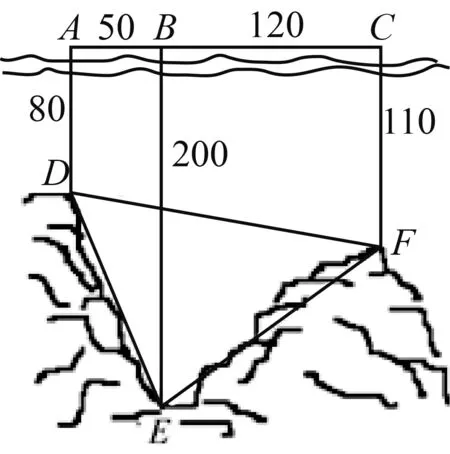
例5如图，为了解某海域海底构造，在海平面内一条直线上的A,B,C三点进行测量. 已知AB=50m，BC=120m，于A处测得水深AD=80m，于B处测得水深BE=200m，于C处测得水深CF=110m，求∠DEF的余弦值.

本题以海底考查测量为背景，将三角函数的知识与平面几何相结合，考查考生运用正弦定理、余弦定理解决实际测量问题的能力.

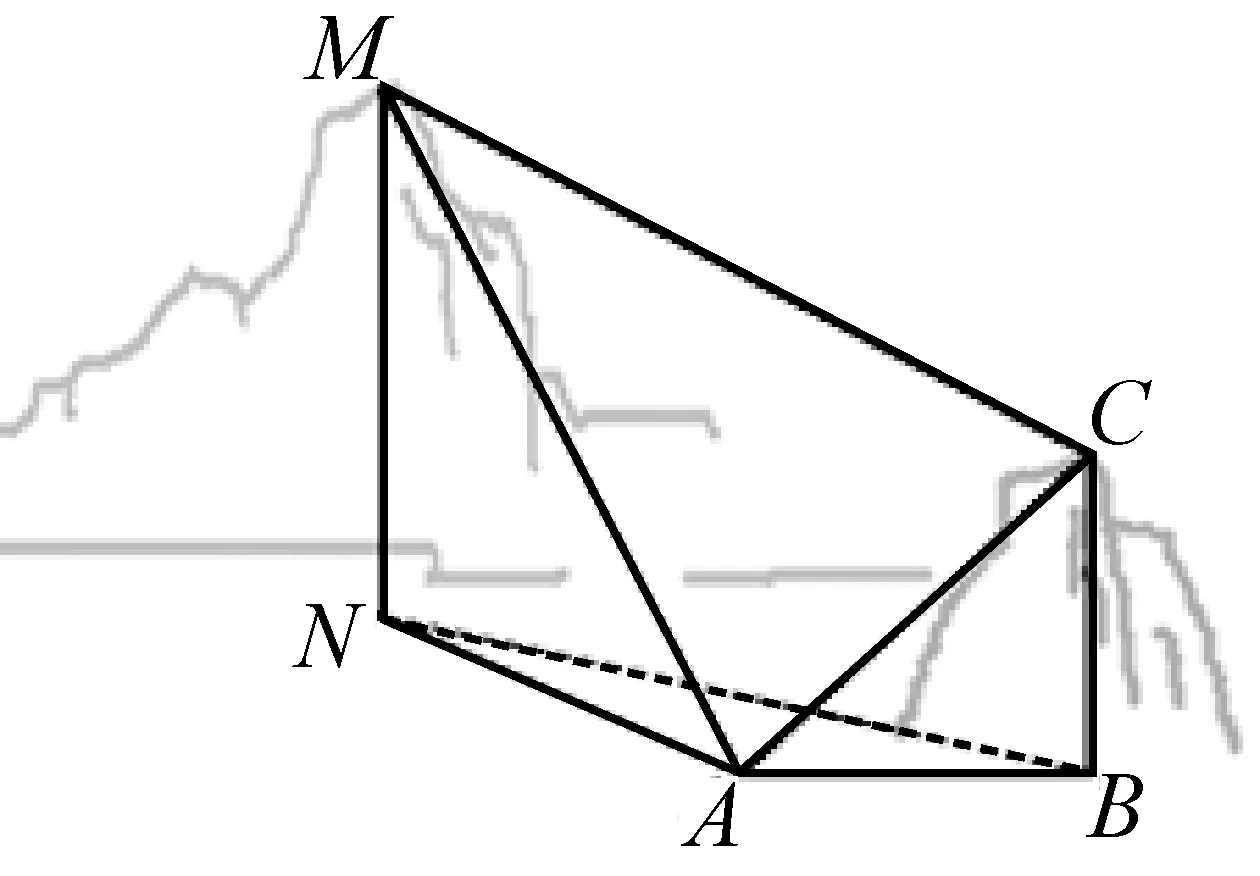
例6如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点. 从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°. 已知山高BC=100m，则山高MN= m.

本题将解三角形与空间位置关系结合在一起，需要考生有一定的综合应用能力，试题的情境是考生熟悉的观测测量问题，试题的另一个背景是空间中的位置关系与度量求解. 本题依据实际情境中两座山的一些测量信息，给出了空间中的三角形的一些具体测量值. 在设计此题的题干时，需要确定哪些数值是可以通过观察点测量得到的，哪些数值是需要通过解三角形的运算求解得到的.

2.4 对创新意识的考查

创新意识是高考的考查重点和特点，高考对创新意识的考查主要体现在，对于社会和自然中存在的各种现象或问题，鼓励考生敢于冲破习惯思维的束缚打破常规发现思考问题或提出理论.在此过程中考生要运用丰富的知识和经验，从各种数据文字资料中获取有用信息，运用判断、归纳、演绎、比较、概括等方法辩证地讨论问题的各个影响因素，提出研究问题的思路和方法步骤，或者提出新的观点、新的发现、新的规律. 三角函数兼具几何与代数两方面的特点，其变式是多种多样的.因此可以充分利用这些特点考查考生的独立思考、分析问题和解决问题的能力，要求考生能够将三角函数的知识应用到问题情境中.

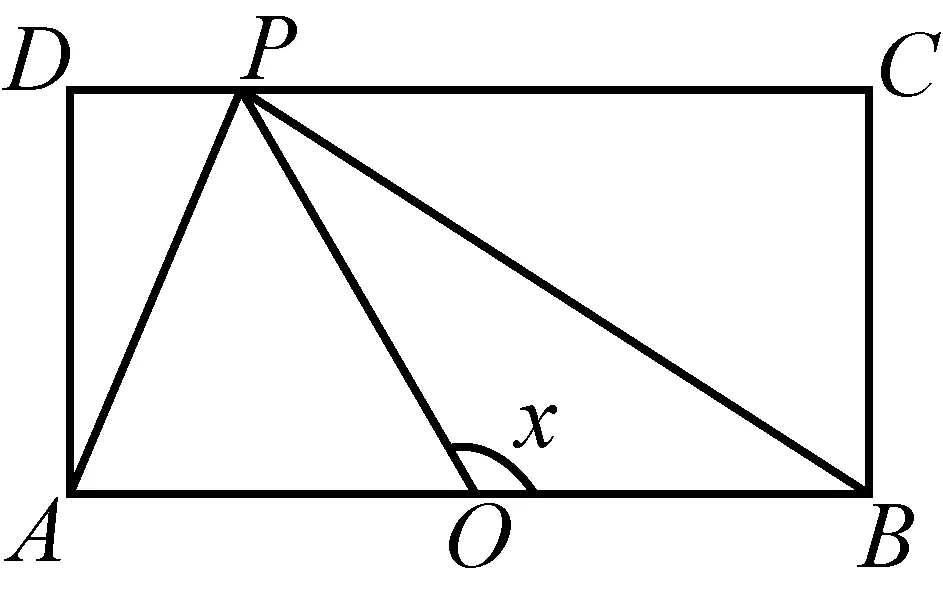
例7如图，长方形ABCD的边AB=2，BC=1，O是AB的中点. 点P沿着边BC，CD与DA运动，记∠BOP=x. 将动点P到A，B两点距离之和表示为x的函数f(x)，则y=f(x)的图像大致为( ).

A

B

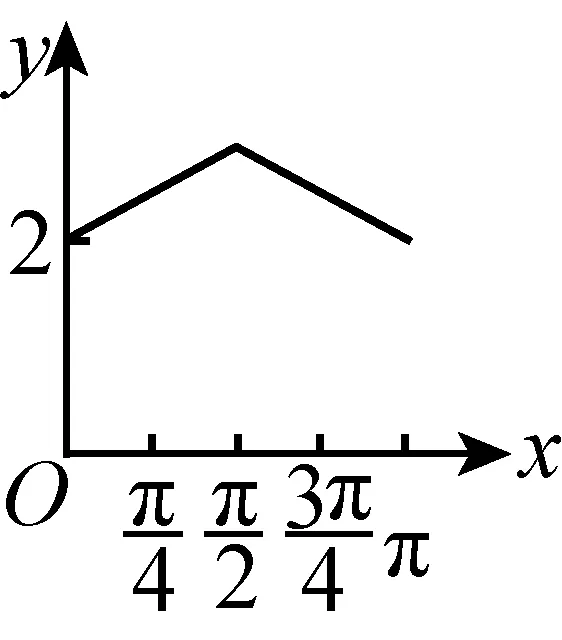
C

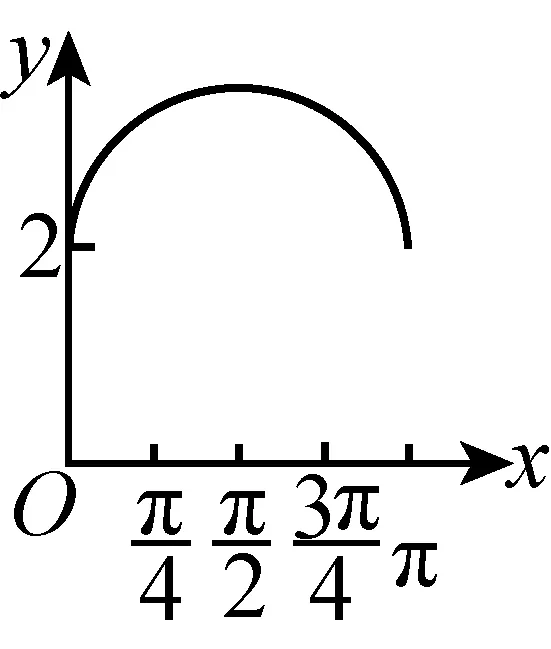
D

本题的题干似乎与三角函数毫不相关，但考生在计算距离时会发现，其形式化表征就是三角函数. 本题的背景是以简单平面几何问题为载体，以距离为桥梁，将几何问题与代数问题联系在一起，这需要考生能全面地认识与把握三角函数的三个组成部分，实现三者间的相互转换. 本题在考查三角函数的图像与性质的同时，考查考生对三角函数的数形结合思想的运用以及基于三角函数的逻辑推理能力，要求考生具有一定的创新意识.

例8在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是__________.

本题给出了四边形的一条边的度量值，以及三个角的大小，是一个局部可解的四边形问题. 考生在解决这个问题时需要注意三角形与四边形之间的横向联系. 本试题的考查目标不是为了获得解四边形的一般法则、原理或公式，而是把解三角形的一般理论、法则与公式运用到一个新的情境中，据此考查考生的创新意识，特别是几何思维能力. 当考生在几何上分析清楚四边形ABCD的各种变化的可能性后，运用解三角形的基本知识与技能即可最后解决问题.

3 对中学三角函数的教学思考和建议

3.1 准确掌握三角函数基本概念

数学概念是数学教学的核心.[2]从数学本身的发展来看，数学概念的来源一般认为有两个方面：一是直接从客观事物的数量关系和空间形式反映而得，二是在抽象的数学理论基础上经过多级抽象所获[3].三角函数知识内容作为高中数学的主体内容之一，具有鲜明的特征. 通常来说，在高中数学课程中，三角函数、解三角形与三角恒等变形是相对独立的三个部分. 从学生的知识获取来看，三角函数是由单位圆引入的，具有函数的性质和特点，同时还有运算的技巧性. 这些特点决定了，在三角函数部分的学习中，应当从整体进行把握，准确掌握其基本概念.

3.2 准确运用三角公式

三角公式是进行变换的重要工具. 通过考后阅卷调研可以发现，学生高考答题中经常出现因公式记忆不准确，导致运算出错的现象. 所以在平时的教学复习中，教师要对高考重点考查的三角公式，要有足够重视. 首先要认真研读《考试大纲》，明确高考要求的数学公式. 其次，对基本公式的教学中，要展现公式的来龙去脉及推导过程. 最后，在公式应用中可以变换多种形式，让学生全方位理解公式并熟练掌握. 鼓励学生用不同的推导方法，加深对公式的认识，把握公式间的联系.

3.3 注重学科综合，关注数学应用

20世纪以来，数学向社会、经济和自然界各个领域的渗透，扩展了数学与实际的接触面．数学科学应用于经济建设、社会发展和日常生活的范围和方式发生了深刻的变化[4]．三角函数部分的内容知识更是如此，章建跃博士就曾指出要在数学整体观指导下，对三角函数的研究对象、内容、过程和方法进行系统设计[5]．从高考对三角函数的考查可以看出，考查形式灵活多变，考查侧重点有所不同. 这是由于三角函数的性质和特点决定的，这部分内容容易与其他部分的数学知识进行结合，更容易与实际情境相结合.在这部分命题实践时，应当注意三个方面的结合：一是问题与已有知识间的联系；二是不同的数学概念及其表征的联系；三是数学知识与实际应用背景间的联系.