铁基超导体的扫描隧道显微镜研究进展∗
2018-11-28顾强强万思源杨欢闻海虎
顾强强 万思源 杨欢 闻海虎
(南京大学物理学院,超导物理与材料研究中心,南京 210093)
铁基高温超导体自2008年发现以来,对其超导电性的研究一直是一个热门的课题.扫描隧道显微镜能够在原子尺度进行表面形貌和隧道谱测量,从微观角度研究电子态密度的信息,是研究超导的重要谱学手段.近年来,在铁基超导电性方面,扫描隧道显微镜实验已经积累了一些有价值的结果,本文进行了总结介绍.铁基超导体是多带多超导能隙的超导体,不同材料的费米面结构有很大的变化.扫描隧道显微镜证明,同时有电子和空穴费米面最佳掺杂的铁基样品超导能隙结构是无节点并带有能隙符号变化的s±波.而进一步的实验发现在没有空穴费米面的FeSe基超导体中也存在能隙符号的相反,对统一铁基超导体的配对对称性提供了重要实验证据.此外,扫描隧道显微镜在研究铁基超导体的电子向列相、浅能带特性、可能的拓扑特性方面,提供了重要的实验数据.本文对上述相关内容进行了总结,并做了相应分析和讨论.
1 引 言
铁基高温超导体自2008年发现[1]以来,部分材料的超导临界温度Tc超过了麦克米兰极限[2](≈40 K),使得铁基超导体成为除铜氧化物以外的第二类非常规高温超导体家族[3].同时,高Tc和毗邻的反铁磁相也表明铁基超导体机理无法在Bardeen-Cooper-Schrief f er的电声耦合(BCS理论)框架下进行理解,说明铁基超导体属于非常规超导之列.在铁基超导体中,铁原子的有效磁矩虽然不大,但是由它引起的反铁磁涨落和超导电性的产生密切相关[4].作为一个典型的多带超导体,铁基超导存在多能隙的特性,而且随着掺杂能带和能隙结构发生很大的变化,使得这个系统的超导电性变得非常复杂[5].加之相图中的结构相变、反铁磁(antiferromagnetic,AFM)相变和向列相(nematic phase)的出现,给理解铁基超导的超导起源研究带来了更多挑战[6].
扫描隧道显微镜(scanning tunneling microscope,STM)能够从原子尺度研究样品表面态密度的信息,具有很高的空间、能量分辨率,还能得到一定动量空间的信息,因此在研究超导材料的性质,尤其是配对对称性方面有着很强的优势.在铁基超导物理研究的十年中,STM领域取得了一系列重要进展,对理解铁基高温超导机理等问题有很大的帮助.本文对STM在铁基超导电性和奇异电子态方面的工作进行总结:简要介绍了STM的工作原理及其对超导研究的作用;总结了STM在不同费米面结构的铁基超导体中对超导配对对称性的研究工作;介绍了一些与超导相关的奇异电子态.
2 STM在超导研究中的应用
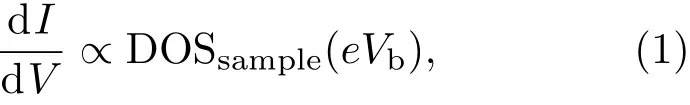
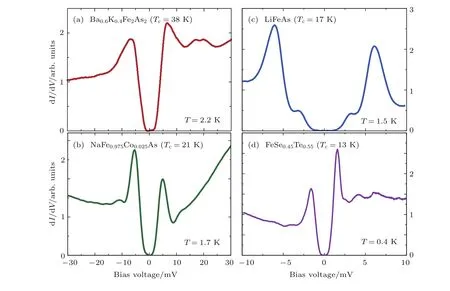
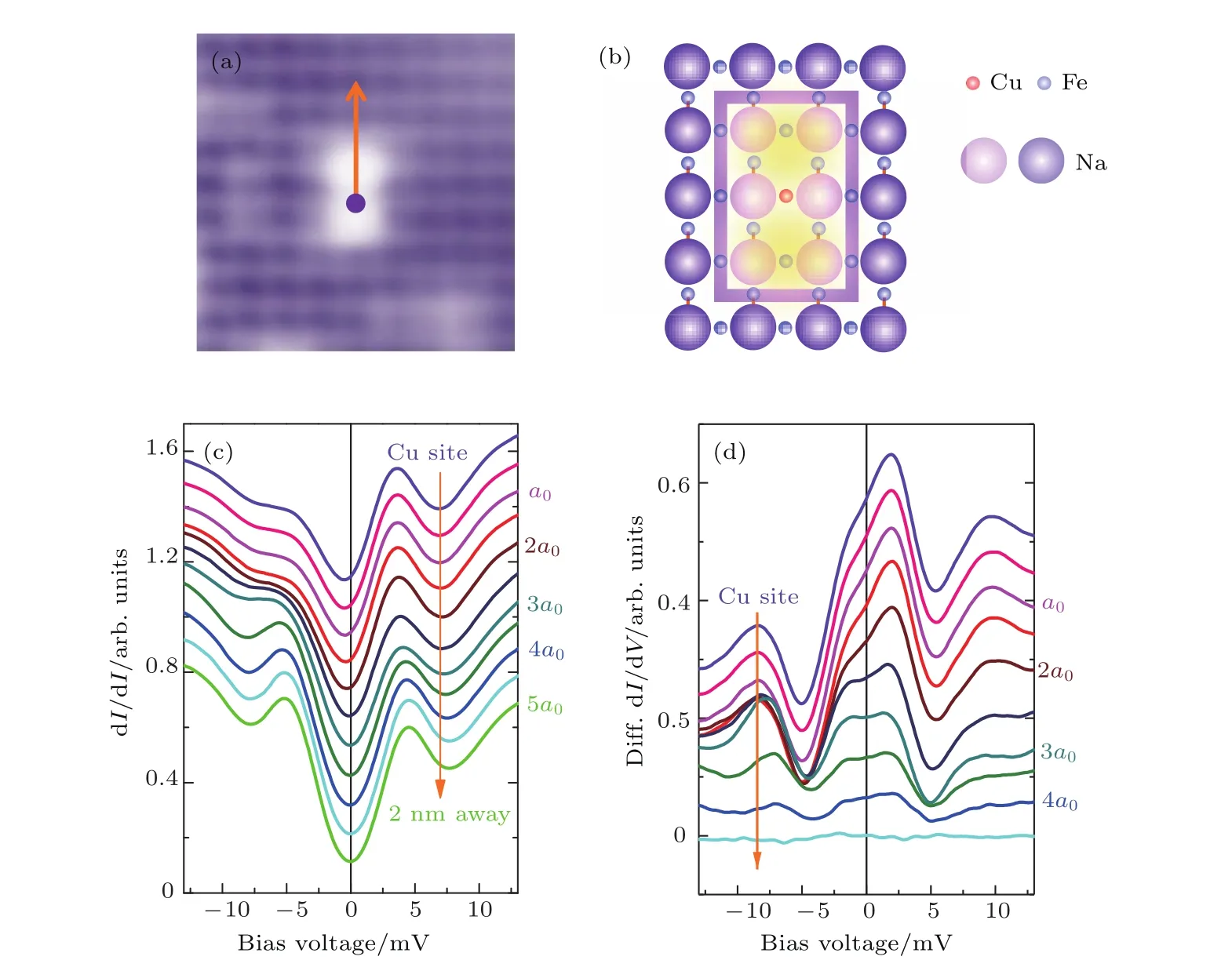
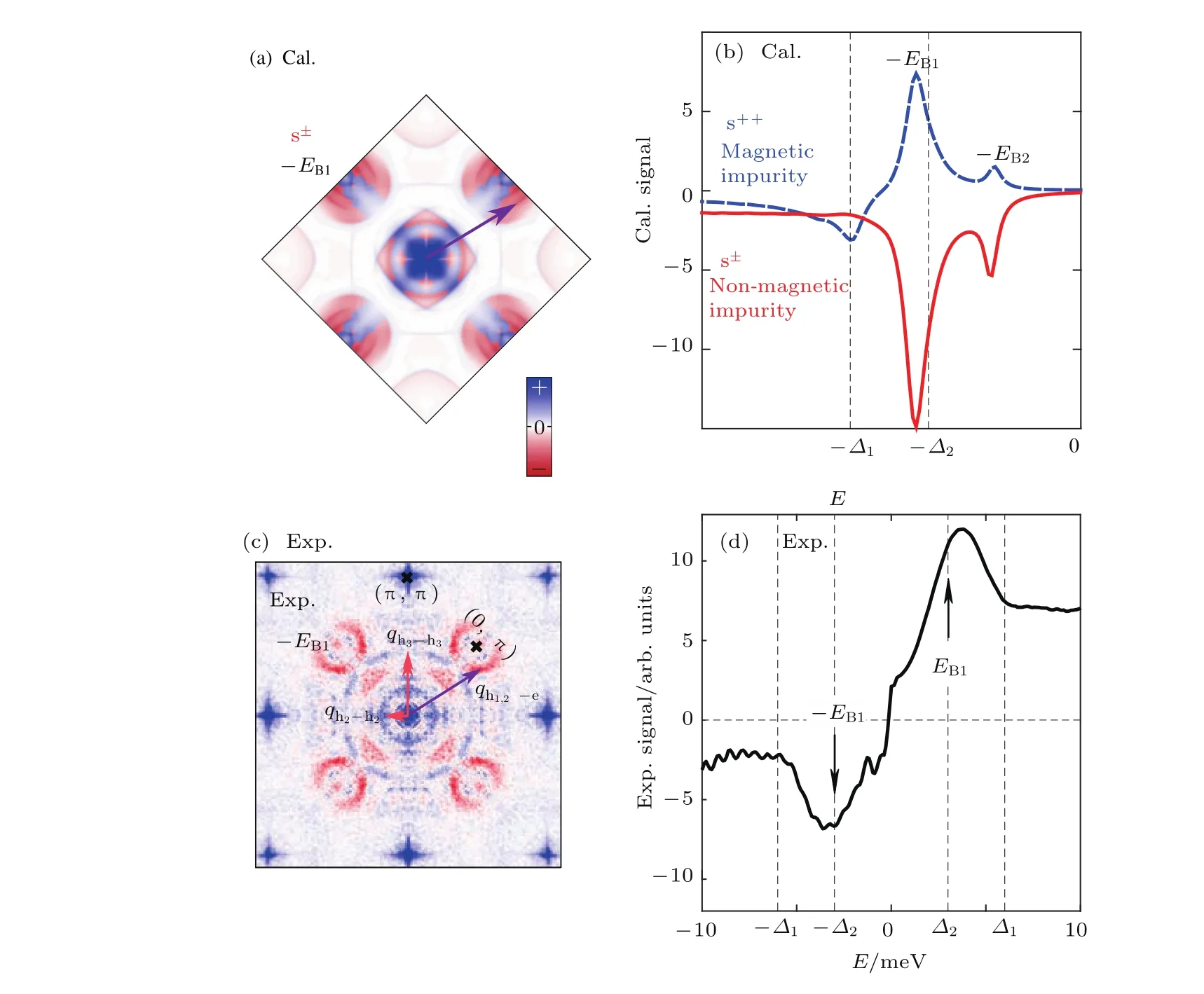
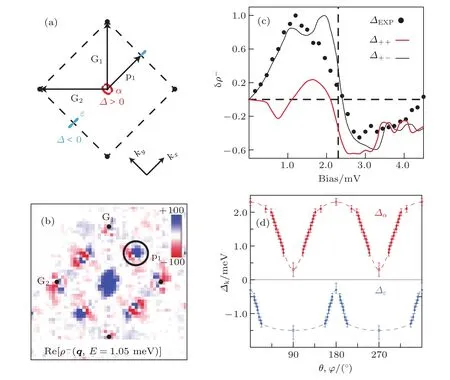
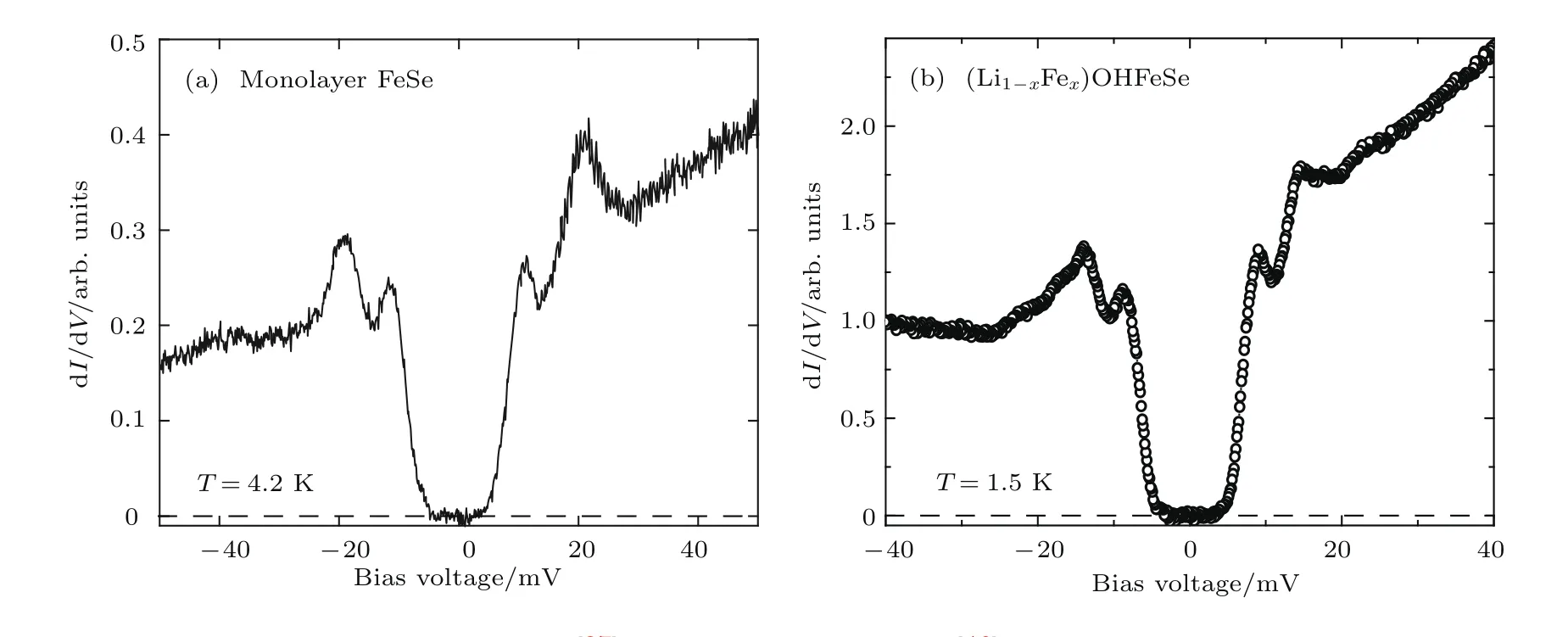
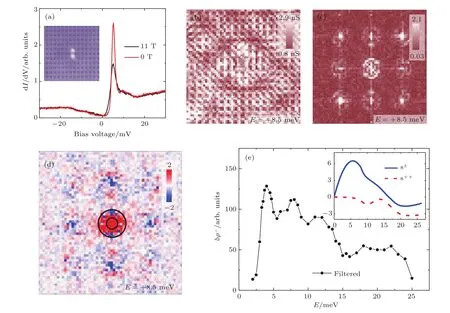
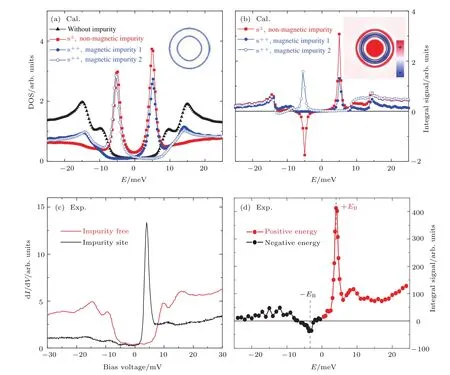
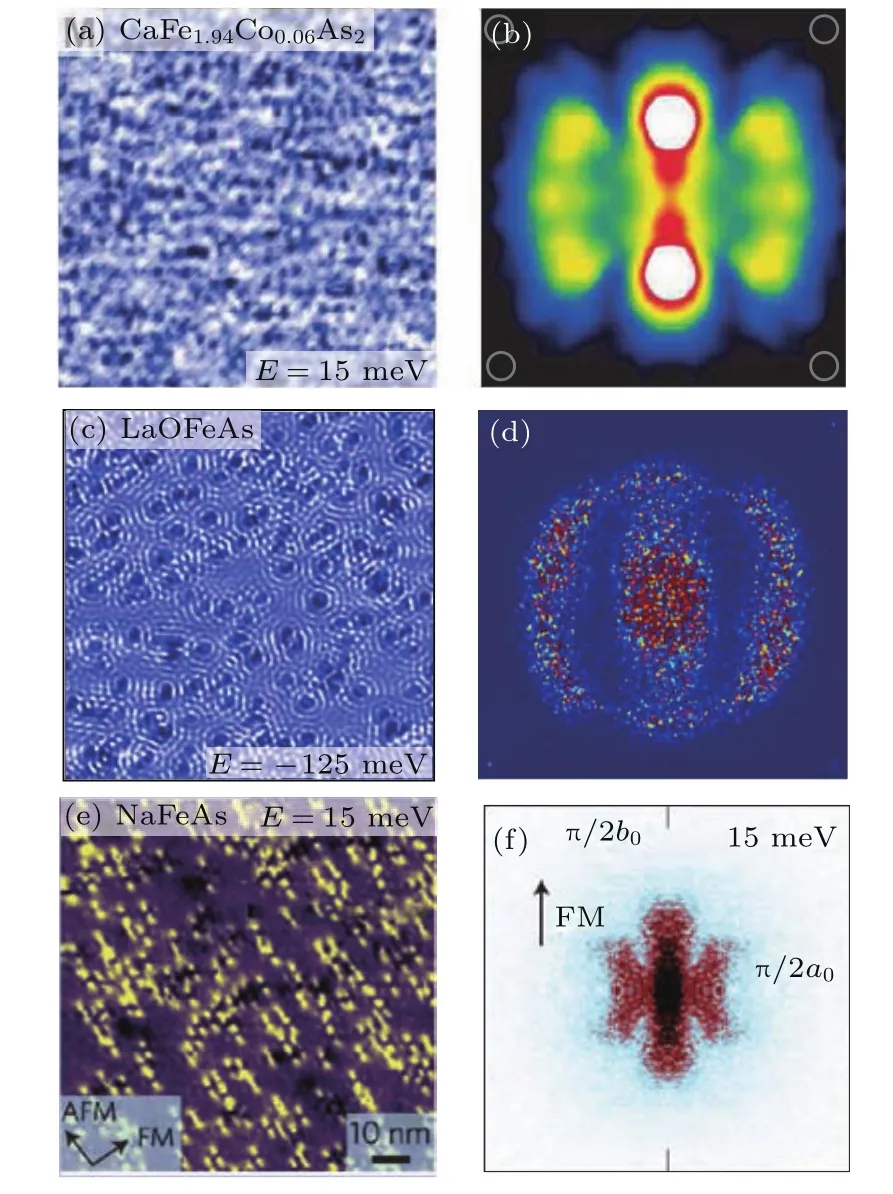
STM是利用量子力学的隧道效应,即当金属针尖和样品非常接近时,加上中间的真空薄层,形成“针尖-真空-样品”隧道结,电子在针尖和样品之间发生单电子量子隧穿效应.在隧道结两边加上电压(bias voltage,Vb),可以测量隧道电流(tunneling current,It).由于针尖尖端可以处理单原子或几个原子,因此该技术具有很高的空间分辨率,能够直接测量样品表面的原子形貌.另外在保持针尖样品距离恒定,通过扫描加在针尖和样品之间的电压,同时测量隧道电流和微分电导(dI/dV),能够获得样品表面微分电导随电压的变化关系(即隧道谱),因此扫描隧道显微镜也被称为扫描隧道谱仪(scanning tunneling spectroscopy,STS).如果假设金属针尖的电子态密度(density of states,DOS)在一定电压范围内随能量变化不大,简化隧穿矩阵元效应,那么测量得到的微分电导将正比于样品在此能量下(eVb,e为元电荷)表面的电子态密度[7],即这里的DOSsample即为样品在离费米能E=eVb时的电子态密度.这一谱学手段对于超导研究来说非常重要.基于BCS理论,两个电子配对形成库珀对,库珀对凝聚形成超导.当电子形成库珀对后,体系的动能有所增加而势能会下降得更多,使总的能量得到降低.在超导态,单电子或准粒子激发满足Bogoliubov色散,即Ek=而εk=}2k2/(2m)−EF,εk是从费米能算起的动能,∆是超导能隙.不考虑散射时,零温极限下准粒子的态密度将在超导能隙内(−∆ 材料的费米面通常用角分辨光电子谱(angleresolved photoemission spectroscopy,ARPES)来测量,它同时有动量和能量分辨.而STM/STS通过对微分电导在实空间分布的测量也可以得到动量空间的信息.周期性晶格中的电子波函数可以用布洛赫波来描述,当晶格中存在杂质、缺陷或者晶界时,这些电子会被散射导致弗雷德尔(Firiedel)振荡,在实空间产生局域态密度的调制,或称为驻波.通过STM测量某个能量E下空间位置的微分电导变化ρ(r,E),即测量样品表面的准粒子相干(qausiparticle interference,QPI)图像,而该图像可以近似地看作样品表面电子态密度的分布.如果对ρ(r,E)进行傅里叶变换(Fourier transform),得到ρ(q,E),这是一个q空间的复数函数,其模值|ρ(q,E)|称为FT-QPI(Fourier transformed-QPI)图案.从动量空间理解,此散射过程可以理解为电子从动量k态被弹性散射到k′态,会造成FTQPI图案上q=k′−k位置处的斑点.散射斑点的强度近似正比于这两点的态密度乘积,即DOS(k,E)·DOS(k′,E),通常被称为联合态密度(joint DOS).在q空间某点得到的ρ(q,E)图案是所有动量差q=k′−k的散射的累积.对于在正常金属上测量得到的FT-QPI图案,除了噪音、杂质态和布拉格散射的信号,主要是态密度较高的费米面波矢之间的散射信号.因此对于正常金属,FT-QPI图案可以由对费米面图像的自关联(selfcorrelation)操作得到模拟的图像,然后和实验测量的FT-QPI图案进行比较.但是需要注意的是,FT-QPI图案得到的是q空间的信息,而不是直接的动量空间的信息,且不能反映费米面在动量空间的具体位置,它需要一定的反演推导才能得到费米面的信息. 对于超导体来说,超导态激发的是Bogoliubov准粒子.Bogoliubov系数,即库珀对未占据和占据±k态的概率幅表达式为: 由上面的公式可知,Bogoliubov准粒子不仅带有动量和能量信息,还携带了超导序参量即能隙的信息.而Bogoliubov准粒子也会被散射中心散射,由费米黄金定则,在简单模型下散射的强度不仅仅正比于散射初态和末态的态密度,还与超导态的相干因子项相关[7].(4)式中对于非磁性散射取“−”号,对于磁性散射取“+”号.因此,对超导态的QPI测量是一个信息丰富的实验技术,可以从中提取超导准粒子的动量和能量信息,甚至还可以得到超导序参量即能隙的信息. 图1 铁基超导体的掺杂相图示意图和不同材料的费米面示意图 (a)从BaFe2As2母体出发分别进行电子和空穴掺杂的相图示意图;(b)FeSe单层膜、Li1−xFexOHFeSe等材料的费米面结构示意图;(c)最佳掺杂Ba1−xKxFe2As2,BaFe2−xCoxAs2,NaFe1−xCoxAs等材料的费米面结构示意图;(d)重度空穴掺杂KFe2As2材料的费米面结构示意图Fig.1.Schematic plot of the phase diagram and Fermi surfaces of iron-based superconductors:(a)The schematic phase diagram of BaFe2As2family by hole doping and electron doping;(b)schematic Fermi surfaces of monolayer FeSe or Li1−xFexOHFeSe;(c)schematic Fermi surfaces of optimally doped Ba1−xKxFe2As2,BaFe2−xCoxAs2or NaFe1−xCoxAs;(d)schematic Fermi surfaces of heavily hole-doped KFe2As2. 铁基超导体的材料体系众多,通过掺杂可以改变样品的费米面结构,并得到不同Tc的超导体.图1(a)显示了以BaFe2As2为母体分别做空穴掺杂(Ba位掺入K)和电子掺杂(Fe位掺入Co)后的相图示意图.其中,BaFe2As2母体是一个反铁磁坏金属而并不超导,在一定温度下发生AFM相变,同时伴随四方到正交的结构相变;随着掺杂增加,体系的巡游性增强,反铁磁相得到压制,AFM相变的奈尔Neel温度减小,超导出现,并在一定掺杂量出现Tc最大值;随着掺杂进一步增加,超导被破坏,Tc降低.铁基超导体的超导相与反铁磁相近邻,两者相互竞争,反铁磁消失的量子临界点附近对应着高Tc超导相,这一现象强烈暗示反铁磁涨落很可能是铁基超导体非常规配对的主要媒介.掺杂影响着铁基超导体的Tc,而且对材料的费米面结构有很大的改变.一些典型铁基材料的费米面示意图如图1(b)—(d)所示,在这些图中,红线表示空穴型费米面,绿线表示电子型费米面.对于一些FeSe基的超导材料,如FeSe单层膜、Li1−xFexOHFeSe等材料,因为在Γ点附近的空穴型能带沉到了费米能以下[8−13],使得布里渊区中心缺失了空穴型费米面,仅在四边M点附近留下了电子型费米面,其费米面结构示意图如图1(b)所示.图1(c)为最佳掺杂的铁基样品(如最佳掺杂Ba1−xKxFe2As2,BaFe2−xCoxAs2,NaFe1−xCoxAs等)的费米面示意图,布里渊区中心Γ点附近为空穴型费米面,M点附近为电子型费米面.图1(d)是KFe2As2材料的费米面结构示意图,由于重度空穴掺杂的缘故,原本Γ点附近的空穴型费米面变得很大,而在M点附近留下“花瓣状”的空穴型费米面[14]. 在铁基最佳掺杂的样品中,电子和空穴费米面大小接近,如图1(c)所示,此时电子与空穴之间的散射波矢为(0,π).实验测量发现[15]自旋极化率在反铁磁特征波矢(0,π)处,在超导临界温度之下出现共振峰值,证明铁基超导的磁配对起源,结合理论理解,说明电子和空穴费米口袋的超导能隙符号会出现反转[16],形成所谓的s±配对态[17,18].这时材料的超导能隙函数在每个费米口袋上仍具有s波对称性,而±表明电子和空穴口袋的超导能隙函数存在反号.由于铁基超导体是一个多轨道系统,另一种观点认为适度的电声相互作用能够增强Fe的3d轨道涨落[19],两电子仍可以通过声子为媒介形成配对,导致s++配对态,其超导能隙函数的符号在整个布里渊区不会产生变化.上述两种配对方式都是无能隙节点的s波超导体,区别在于电子和空穴口袋上的超导能隙是否有变号行为.对于能隙函数没有节点这一问题,可以由STM测量到的隧道谱很好地证明.如图2所示,在一些既有电子又有空穴型费米面的铁基超导体中,隧道谱在零能附近完全没有正常态的准粒子态密度,隧道谱在能隙之间的底部也呈现出英文字母“U”的形状.但是,能隙相反这个问题却不容易直接证明.这里需要注意的是,图2所示的隧道谱在正负能量有些不对称,相干峰等也不对称,这可能是由多带情况下的电子和空穴能带都比较浅,而且费米能不一样造成的. 图2 同时有电子空穴费米面的几个典型铁基超导体表面沿c-轴方向测量的隧道谱Fig.2.Tunneling spectra measured on the surfaces of some typical iron-based superconductors with both electron and hole Fermi pockets,the tunneling current is injected along c-axis. Hanaguri等[20]在Fe(SeTe)上进行了加场前后的QPI测量,主要结果如图3所示.Fe(SeTe)同时有电子和空穴型费米面,费米面大小相似,在FT-QPI图案上得到的主要散射为电子-空穴口袋间的q2散射和电子-电子口袋间的q3散射,如图3(c)所示.如果考虑到电子和空穴费米口袋上的能隙符号相反,即s±配对,那么q2对应异号能隙费米口袋之间的散射,q3对应同号能隙费米口袋之间的散射.如图3(a)所示,在测量得到的零场下FT-QPI图案中可以看到,q2散射斑纹较强,而q3散射斑纹较弱.简单地从(2)式和(3)式出发,当能隙符号相反时,Bogoliubov系数uk和vk反号,而能隙符号相同时uk和vk同号.而样品中广泛分布的缺陷或者杂质作为非磁性杂质对Bogoliubov准粒子进行了散射,根据(4)式定义,此时相干因子I(k,k′)=|uku−vkv′|2.因此,对于同号散射相干因子较小,而异号散射相干因子较大,这是电子空穴费米面能隙符号相反的第一个证据.当加了10 T磁场后,磁通芯子可以认为是磁性散射中心,同上面的分析,序参量异号的散射会被抑制,而同号散射会被增强.实际测量的结果如图3(d)所示,与预期相符合,因此证明了Fe(SeTe)体系中电子和空穴型口袋间的能隙符号相反.但是,由于q3散射斑点和布拉格点重合,特征散射斑纹没有外围圈,该结论受到一些理论上的质疑[21].其中,关于特征散射斑纹没有外围圈,进一步的研究解释为Fe(SeTe)中电子和空穴费米口袋比较小,再加上费米口袋有一定的动量空间宽度,使得散射特征图案没有出现外围圈,而保留有中间很亮的斑[22]. 图3 Fe(SeTe)磁场下FT-QPI图案中不同散射斑纹强度的变化 (a),(b)分别在零场和10 T磁场下得到的FT-QPI图案;(c)Fe(SeTe)费米面以及主要的口袋间散射通道示意图;(d)图(b)减图(a)得到的FT-QPI受到磁场影响的结果,红色为信号减弱,蓝色为信号增强[20]Fig.3.Magnetic f i eld dependent intensity of dif f erent kinds of characteristic scattering spots on FT-QPI patterns measured in Fe(SeTe):(a),(b)FT-QPI patterns measured at 0 T and 10 T,respectively;(c)a schematic plot of Fermi surface and inter-pocket scatterings in the momentum space;(d)the intensity dif f erence of characteristic scattering spots by subtracting(a)from(b)[20]. 图4 非磁性铜杂质诱导的能隙内束缚态 (a)STM测量得到Cu掺杂原子上方表面Na原子的形貌;(b)掺杂Cu原子对表面Na原子影响的示意图;(c)沿图(a)中箭头测量的一系列隧道谱;(d)减去远离杂质点2 nm的隧道谱得到的微分电导谱差随空间的演化[28]Fig.4.In-gap bound state induced by the non-magnetic Cu impurity:(a)The topography of the Na atoms on the surface above a Cu impurity;(b)illustration for atoms near a Cu impurity site;(c)tunneling spectra measured along the arrowed line shown in(a);(d)the dif f erence tunneling spectra by subtracting the spectra with that measured 2 nm away from the Cu site[28]. 非磁性杂质产生的束缚态也可以用来判定超导能隙函数的形式.从著名的安德森理论[23]出发,对于没有能隙符号反转的超导体,磁性杂质与巡游电子之间产生磁交换作用,导致配对电子的自旋翻转,从而破坏超导,并产生费米能附近的Yu-Shiba-Rusinov杂质共振态[24];而非磁性杂质很难对普通s波超导体产生实质性破坏作用,有限的势散射无法对电子配对散射过程产生明显影响,不会形成费米能附近的杂质共振态[24].而对于有能隙符号反转的超导体中,如d波铜氧化物超导体中,非磁性杂质会造成能隙内的很强的杂质态峰[25].在铁基超导体s±配对态下,理论计算表明,合适的非磁性杂质散射势(∼1 eV)也会产生杂质束缚态的峰[26].通常认为,铁基超导体中的铁离子是没有磁性的,而钴、镍等掺杂原子进入晶格形成离子态后,其性质和铁离子态是接近的,因为多余的d电子加入到巡游电子之列,因此通常也被认为没有磁性.实验上,当非磁性杂质的散射势比较小时,例如Na(Fe1−xCox)As中的Co杂质,杂质诱导的杂质态将靠近超导相干峰,在零能附近不能观察到杂质束缚态[27].从最佳掺杂的Na(Fe1−xCox)As材料出发,进一步掺入Cu杂质,利用磁化测量判定了铜原子是非磁性或弱磁性杂质[28].利用STM可以找到掺杂的Cu原子所在的位置,测量到的Cu原子上方表面Na原子形貌如图4(a)所示,结合原子分布示意图4(b),可以判定高亮双锤形的亮斑中心位置下方应该是一个掺杂的Cu原子.隧道谱的测量表明,Cu杂质对隧道谱在能隙内的谱形影响很大,如图4(c)所示.而当把远离杂质点测量的隧道谱作为背景减掉,可以得到能量依赖的微分电导差,如图4(d)所示,从图中可以清晰地看到非磁性杂质Cu原子诱导出了能隙内的杂质态,并与基于s±配对下的理论计算结果一致,作为一个较为坚实的实验证据,证明了该材料的s±超导配对的对称性[28]. 前面提到,超导Bogoliubov准粒子含有超导序参量的信息,在FT-QPI散射强度的计算过程中需要考虑相干因子的作用.傅里叶变换得到的复函数ρ(q,E),不仅有强度即|ρ(q,E)|,还有相位θq,E,即ρ(q,E)=|ρ(q,E)|eiθq,E. 而对于Bogoliubov准粒子散射过程,θq,E也含有超导序参量的信息.几位理论学家Hirschfeld,Altenfeld,Eremin和Mazin提出了相位敏感的QPI分析方法[29],这里把这一方法简称为HAEM的QPI方法.该方法考虑一个非磁性杂质(散射势为U)放置在实空间QPI图像的中心位置,相位参考量是FT-QPI正负能量的反关联部分,即ρ(q,+E)−ρ(q,−E).理论上,当杂质在实空间图像中心且实空间图像是中心对称时,如果做傅里叶变换,根据傅里叶变换的定义,FT-QPI的信号ρ(q,E)将为实数[22].在此情形下,对于两个费米面两个超导能隙∆1和∆2(|∆1|>|∆2|)的情况,对包含两个费米面之间散射波矢的q空间区域S进行积分,可以得到半定量的表达式[29]: (5)式中Re代表实部,Im代表虚部.从(5)式可以看出,如果∆1∆2>0,即对于两个费米面上的超导序参量同号的s++配对态,δρ−(E)在两个能隙之间(|∆2| 图5 HAEM方法理论计算得到的不同超导能隙结构和不同温度下的相位敏感QPI信号δρ−(E)[29]Fig.5.Calculation results of phase-referenced QPI signal δρ−(E)in superconductors with dif f erent gap symmetries at dif f erent temperatures by HAEM’s method[29]. 图6 DBS-QPI方法基于LiFeAs能带结构理论计算和在LiFeAs样品上实验测量的相位参考的QPI结果[32,33]Fig.6.Calculation and experimental results of phase-referenced QPI signal δρ−(E)in LiFeAs by DBS-QPI method[32,33]. 最近,Chi等[32,33]又提出了新的相位参考QPI方案,该方案基于实空间QPI图像中心的单杂质产生的能隙内束缚态,简称为DBS-(defect bound state)QPI方法.该方法以正负能量的FT-QPI信号为幅值,而正能量下的相位θq+E为参考相位,定义正负能下的相位参考量表达式为[32]:根据(6)式的定义,gpr(q,+E)始终是正值,而gpr(q,−E)是真正相位参考的量.该文献指出,对于无磁性杂质在s±配对的情况下,散射前后波矢所对应的能隙符号相反,对应的散射相位参考项cos(θq,−E− θq,+E)是−1;而对于s++配对,其值是+1.这里的能量是指束缚态峰值的能量.该结论是否具有广泛性还未见理论推导.不过作者以LiFeAs材料为对象进行了数值计算,计算结果如图6(a)和图6(b)所示.计算LiFeAs上的杂质在能隙内产生了两个束缚态,能量位置分别在EB1和EB2.图6(a)是对相位参考项gpr(q,−EB1)的计算结果,其中箭头所示的斑纹为电子和空穴口袋之间的散射区域,主要为负值.对于gpr(q,E)在上述散射区域进行积分得到gpr(E),结果如图6(b)所示.可以明显地看到,s±配对下的非磁性杂质和s++配对下的磁性杂质,gpr(E)的结果有很大的差别:对于磁性杂质,同号超导能隙费米口袋之间的散射在杂质束缚态能量处的gpr(−E)信号为正;而对于非磁性杂质,异号超导能隙费米口袋之间的散射在杂质束缚态能量处的gpr(−E)信号为负.这里需要注意的是,对于s++配对的超导体,非磁性杂质不会出现能隙内明显的束缚态的峰,因此未做相关讨论.当杂质在中心且实空间图像中心对称的理想情况下,ρ(q,E)为实数,θq,E取0或π,因而相位差θq,−E−θq,+E也为0或π.根据数值计算可以得到这样的结论:对于非磁性杂质造成的s±配对费米口袋之间的散射,正负能量的散射相位相反,即|θq,−E− θq,+E|= π.Chi等[33]还在实验上对LiFeAs的QPI进行了相关测量和分析,结果如图6(c)和图6(d)所示,可以发现此时相位参考量gpr(−E)在其中一个束缚态能量−E=−EB1附近有个负值的峰,与s±配对下的非磁性杂质结果定性一致,他们确定LiFeAs材料中的电子空穴口袋能隙存在反号[33].而进一步基于(7)式,在多杂质且无明显杂质束缚态的情形下,DBS相位参考方法也能用来有效判定其他非常规超导材料的配对对称性[22,34]. 图7 不同实验组测量的FeSe单晶超导隧道谱 (a)FeSe多层膜上测量的结果[39];(b)FeSe单晶上测量的结果[40];(c)更低温度下FeSe单晶的数据[30]Fig.7.Tunneling spectra measured on FeSe by di ff erent groups:(a)Tunneling spectra measured on FeSe thick fi lm[39];(b)tunneling spectrum measured on FeSe single crystal[40];(c)tunneling spectrum measured on FeSe single crystal at a lower temperature[30]. FeSe是铁基超导体中具有最简单结构的材料[35],临界温度在9 K左右,但是该材料和FeAs体系材料不一样的是,在90 K左右仅仅有结构相变,但是在超导转变温度之上却未发现反铁磁相变.FeSe单晶在加压后最高Tc可达37 K[36],而在FeSe单层膜中发现了较大能隙[37],直接的电阻测量发现Tc甚至超过了50 K[38].上述这一系列新奇的物理现象使得FeSe这一材料备受关注.对于FeSe厚膜材料[39]和单晶材料[40]的早期STM隧道谱研究发现,在费米能附近,隧道谱谱形呈现“V”形,如图7(a)和图7(b)所示,说明该材料中可能存在能隙节点.但是随后的一些实验,如低温比热[41,42]、微波光导[43]、热导[44]、穿透深度[45]等测量,都表明FeSe单晶是一个无能隙节点但存在能隙极小的多能隙体系. 2017年,Sprau等[30]将测量温度降到280 mK,发现零微分电导不只是发生在费米能位置,而是一个很小的能量范围,如图7(c)所示,并确认能隙最小值&150µeV,排除了有能隙节点的d波配对对称性.他们还进行了更为精细的QPI测量,并用HAEM的相位参考方法来判定超导能隙正负号是否发生变化.图8(b)显示了HAEM相位参考项δρ−的图,可以发现p1散射斑纹,即起源于空穴型α口袋和电子型ε口袋之间散射,基本为正值.进一步对包裹p1散射斑纹的圆圈内区域信号进行积分,如图8(c)所示,实验数据与理论计算在s±模型下得到的结果定性一致,因此判定该材料中存在能隙符号相反.结合细致的QPI分析得到具体的能隙数值,在图8(d)中他们给出了考虑到能隙正负号后空穴型α口袋和电子型ε口袋的能隙随角度的变化关系. 图8 FeSe单晶的QPI测量和能隙相反的实验证据 (a)FeSe单晶发生结构转变后的费米面示意图;(b)单杂质QPI数据得到的HAEM方法的相位参考量δρ−(qE=1.05 meV);(c)对电子-空穴口袋之间散射,即图(a),(b)中的p1散射斑纹进行积分,得到的实验结果和理论计算比较,结果和s±配对理论曲线定性相符合;(d)最终得到的两个费米口袋上能隙随角度的依赖关系[30]Fig.8.QPI experimental results and resultant gap function obtained in FeSe single crystal:(a)Schematic plot of Fermi surfaces below the structural transition temperature in FeSe;(b)calculated phase-referenced term δρ−(qE=1.05 meV)from the QPI data measured around a single non-magnetic impurity by HAEM’s method;(c)comparison between the experimental data and theoretical calculation results of δρ−(E)for the inter-pocket scattering spot p1between hole-like α and electron-like ε pockets,which conf i rms the s± pairing in FeSe;(d)angle dependence of superconducting gaps along the two Fermi pockets[30]. 在3.1节曾经提到,对于一些FeSe基的超导体,如FeSe单层膜、Li1−xFexOHFeSe等材料,因为在Γ点附近的空穴费米口袋沉到了费米能以下,仅在M点附近留下电子型费米口袋,费米面结构如图1(b)所示.但是,对于s±配对模型,能隙变号发生在空穴型费米口袋和电子型费米口袋之间,而空穴费米面的缺失,似乎动摇了基于上述费米面结构提出的s±配对模型的基础.然而,如果反铁磁涨落仍然是这类FeSe基超导体电子配对的媒介,那么超导序参量必须存在反号,因此需要进一步的实验来统一有和没有空穴费米面存在的铁基超导体的能隙形式. 图9(a)和图9(b)分别显示了在FeSe单层薄膜[37]和Li1−xFexOHFeSe单晶[46]上测量的隧道谱,可以发现这两个谱形极为相似:零能附近“U”形隧道谱表明体系没有能隙节点,有两对相干峰,对应着两个超导能隙.但是早期的ARPES实验发现[8−11],这两种材料上只有一套电子型的费米面,那么两个能隙如何存在于一套费米面是个令人困扰的问题.对于Li1−xFexOHFeSe材料,相干峰位置约为14.3 meV和8.6 meV.通过对隧道谱的拟合分析发现,这两个能隙都需要是各向异性的,而能隙最大值对应着14.3 meV和8.6 meV. 图9 FeSe单层薄膜[37]和Li1−xFexOHFeSe单晶[46]上测量的超导隧道谱Fig.9.Tunneling spectra measured on monolayer FeSe[37]and Li1−xFexOHFeSe single crystal[46]. 图10 Li1−xFexOHFeSe的QPI测量和费米面及能隙结构 (a)14.5 meV的FT-QPI图案;(b)费米面示意图;(c)图(b)中费米面的自关联模拟;(d),(e)小能隙和大能隙的最大值处测量的FT-QPI图案中心斑纹;(f)杂化后两个电子口袋的轨道成分以及能隙分布[46]Fig.10.QPI results and Fermi surface of Li1−xFexOHFeSe:(a)FT-QPI pattern at 14.5 meV;(b)schematic plot of Fermi surface;(c)self-correlation of the Fermi surface shown in(b);(d),(e)FT-QPI pattern for the central spot measured at 8.6 and 14.5 meV;(f)orbital contents and gap maxima along the two electron pockets with hybridization[46]. 进一步用STM对Li1−xFexOHFeSe材料进行QPI测量,FT-QPI图案如图10(a)所示.图10(c)是对图10(b)的费米面示意图进行自关联来模拟FT-QPI图案,与图10(a)非常相似,证明了该材料中空穴费米面的确缺失了.通过细致的不同能量下的中心斑纹的QPI测量[46],可以发现杂化形成的内外两套费米口袋,与后来的精细的ARPES结果发现的两套嵌套的电子型费米口袋的结果[47]较为一致.进一步在不同能量下的测量发现内套散射环随着能量升高先出现,在小能隙最大值8.6 meV附近,如图10(d)所示,外套散射环开始出现,在大能隙14.3 meV处,内外环都显示出来.通过分析认为,小能隙对应内套的电子型费米口袋(dxz/yz轨道成分为主),而大能隙对应着外套电子型费米口袋(dxy轨道成分为主),示意图见图10(f).虽然分辨出了杂化形成的内外两套费米面,分别与小大两个能隙相对应[46],但是对于这两个能隙符号相反,还需要其他方法确定. 图11 Li1−xFexOHFe1−yZnySe超导能隙符号的HAEM相位参考方法的甄别 (a)杂质点零场和11 T磁场下的隧道谱,插图是该哑铃状杂质的形貌;(b)图(a)插图所示区域的QPI测量结果,即微分电导图ρ(r,E=+8.5 meV);(c)图(b)傅里叶变换后的FT-QPI图案;(d)相位参考量δρ−(q,E=+8.5 meV)的结果,图中的两个圆圈之间的区域包含两电子口袋间的主要散射,是δρ−(q,E)的积分区域;(e)δρ−(E)的积分实验曲线,插图是s±配对态和s++配对态的理论计算结果[31]Fig.11.Determination of the sign-reversal order parameter in Li1−xFexOHFe1−yZnySe by HAEM’s phase-referenced QPI method:(a)Tunneling spectra measured at the impurity site under a magnetic f i eld of 0 T and 11 T,respectively;(b),(c)QPI image ρ(r,E=+8.5 meV)and FT-QPI pattern ρ(q,E=+8.5 meV)measured at the area as shown in the inset of(a);(d)the phase-reference term δρ−(q,E=+8.5 meV)and the region within the two circles contains most of the signals from inter-and intra-pocket scatterings which is used as the integrated region of δρ−(q,E);(e)the experimental result of integral δρ−(E),and the inset shows the theoretical calculation results of integral signal for s± and s++pairing[31]. Zn杂质通常为非磁性的杂质,人为地在Li1−xFexOHFeSe中引入了少量的Zn杂质,可能占据在FeSe层的Fe位.虽然掺杂后Tc有所下降,但是在远离杂质点位置测量的超导隧道谱与无掺杂样品上测量的结果类似.图11(a)的插图显示了Zn掺杂样品中孤立的杂质周围的表面形貌,在这里为了进行相位参考的QPI操作,杂质被严格移动到了视图中心.通过隧道谱的测量,如图11(a)所示,该杂质点在零场下的隧道谱表现出很尖锐的能隙内束缚态,而11 T的外加磁场仅仅压制了杂质态的峰高和延展了杂质态的峰宽,并没有移动杂质态峰的能量[31].如果该杂质是磁性的,磁场会与其自旋作用发生明显的塞曼效应[24],对杂质态的能量造成移动,简单计算1/2自旋在11 T磁场下大概移动0.64 meV,如果有该能量大小的移动是完全可以被STM分辨出来的.而磁场下的杂质态峰位置没有移动,证明该杂质是非磁性的.根据前面3.2节的讨论,如果非磁性杂质能够在超导能隙内诱导出杂质态,这本身就说明了该材料具有反号的超导序参量[24].进一步的实验证明应用3.4节提到的HAEM相位参考方法进行测量,图11(b)和图11(c)分别给出典型的QPI图像ρ(r,E =8.5 meV)和FT-QPI图案|ρ(q,E=8.5 meV)|, 其中FT-QPI图案和图10(a)所示的未掺杂样品上测量的结果类似,证明掺杂并没有明显改变费米面结构,空穴型费米面仍然缺失.应用HAEM相位参考方法的(5)式,可以计算出δρ−(q,E=8.5 meV),如图11(d)所示.其中两个圆圈中间区域包含了两电子口袋的大部分散射通道强度,而这部分信号大部分是正的,且有较大数值.积分两个圈之间的信号得到的δρ−(E)绘于图11(e)中,可以看出,实验结果的曲线和基于s±配对的理论计算基本相符,和基于s++配对的理论计算结果有很大的区别.因此,上述结果表明在Li1−xFexOHFeSe系统中,两个电子型费米口袋间能隙符号出现反转.因为证明了该杂质是无磁性杂质,对于无磁性杂质,s++配对模式是不会出现能隙内的杂质态,因此该结果可以排除s++能隙.此外,从隧道谱上在零能附近看见的是“U”形的,因此可以排除节点型d波.对于无节点的d-波(nodeless d-wave)的情况,也不能得到解释,因为所测量的结果是费米口袋内的小动量转移散射行为,从而对于每一个费米口袋,能隙符号都是一致的,所以也可以排除无节点d波.从而确认了该材料的s±配对机理. 图12 Li1−xFexOHFe1−yZnySe超导能隙符号的DBS相位参考方法的甄别 (a)基于插图费米面结构不同配对对称性下计算出来的隧道谱;(b)理论计算出来的相位参考量gpr(q,±E)在q空间的积分结果;(c)实验测量的某个杂质附近和远离杂质的隧道谱;(d)实验测量并积分出的相位参考量gpr(±E)随能量的变化[48]Fig.12.Determination of the sign-reversal order parameter in Li1−xFexOHFe1−yZnySe by DBS phase-referenced QPI method:(a)Calculated tunneling spectra at the impurity site and some impurity-free place in superconductors with dif f erent gap symmetries;(b)energy dependent integral signal of phase-referenced term gpr(q,±E);(c)tunneling spectra measured at the impurity site and some impurity-free place in Li1−xFexOHFe1−yZnySe;(d)integral signal of the measured phase-referenced term gpr(q,±E)[48]. 另一种相位参考的DBS-QPI方法同样在Li1−xFexOHFe1−yZnySe材料中适用,基于仅有内外电子口袋的计算结果(如图12(a)和图12(b)所示[48])可以看出,计算结果定性地与既有电子又有空穴口袋的LiFeAs材料中的结果(图6(b))一致.而实验测量的隧道谱中(如图12(c)所示),杂质态峰在正能非常强,负能相对较弱,不随磁场移动的杂质态峰证明该杂质同样为非磁性杂质.实际测量并积分得到的gpr(±E)结果如图12(d)所示,可以发现,在负杂质态峰能量处,积分信号出现了一个负的峰,和s±配对非磁性杂质的理论计算定性一致.同时这一实验在不同类型的非磁性杂质和多杂质的情况下也得到了相同的结论,证明该材料中能隙符号的确发生了变化[48]. 结合中子散射在Li1−xFexOHFeSe材料中的数据,可以进一步讨论并确定该材料中两个符号相反的能隙如何具体对应到两套杂化形成的内外两套电子型费米口袋上[49],这里不再赘述.在Li1−xFexOHFe1−yZnySe材料中的结果,证明了只有电子型费米面的铁基超导材料中也存在着能隙符号的变化,说明了排斥势导致的配对相互作用(很有可能是交换反铁磁涨落)是铁基超导体配对的主要原因.最近,在具有相同电子结构的FeSe单层膜中,利用STM研究发现了隧道谱上的玻色模,因此配对机理倾向于磁激发的机理[50],另外输运研究中发现的线性磁阻行为也给出了自旋涨落的可能性[51].上述工作为统一重度电子掺杂中配对对称性的起源提供了重要的实验参考. 对于铁砷基超导体的母体,在高温时其晶格结构是四方相,随着温度的降低,晶格将会发生从C4到C2的对称性转变,变成正交相.当温度略低于结构相变温度,系统发生反铁磁相变.虽然结构相变会影响电子态密度分布的各向异性,但是在母体中测量得到的二度对称的电子激发行为无法用正交相的晶格结构所完全解释,这样二度对称的电子相被称为电子向列相(nematic electronic structure).最早电子向列相由STM在接近母体的掺杂CaFe1.94Co0.06As2材料上发现[52],在15 meV测量的特征电子结构如图13(a)所示,电子态在横轴方向有些拉长的长条.对实空间电子态做自关联,得到的图像会出现长度为8倍于Fe-Fe原子间距aFe-Fe的斑纹[52].图13(b)显示的是与图13(a)对应的FT-QPI图案,可以发现,FT-PQI图案也表现出明显的二度对称性,三个竖条状斑纹在q空间的距离也和实空间8aFe-Fe对应.这是铁基超导母体电子向列相的实验证据,而且与表面重构无关.之后,在LaOFeAs等[53],NaFeAs[54]材料中也相继发现了类似的二重对称性的电子态行为,如图13(c)—(f)所示,而且这些二度对称的电子态随着能量的变化还有一定的色散关系.上述这些不同体系内进行的STM实验证明了铁基超导母体中的电子向列相的普遍性.开始是微观观测发现电子向列相,后来由各向异性的电阻测量[55,56]等实验进一步证实,并且发现在母体中电子向列相的温度甚至高于结构相变的温度[57],出现所谓向列相的涨落.电子向列相的起源还有一定的争议,有包括结构相变、反铁磁涨落、轨道涨落这三个可能的原因[58].这一奇异的电子态和超导有一定的关系,并且丰富了铁基超导体的电子态相图. 图13 铁砷基超导母体CaFe1.94Co0.06As2样品[52],LaOFeAs样品[53]和NaFeAs样品[54]中测量得到的QPI图像和相应的FT-QPI图案Fig.13.QPI images and FT-QPI patterns for the parent compounds of FeAs-based superconductors Ca Fe1.94Co0.06As2[52],LaOFeAs[53]and NaFeAs[54]. 如前所述,FeSe单晶结构简单,且随着温度的降低只发生结构相变而没有反铁磁相变,当温度低于结构相变后,体系的电子空穴费米口袋将会有很强的二度性.如前所述,该二度性甚至会影响到超导能隙的各向异性[30].在此情况下,研究FeSe材料中的电子向列相行为将是一个比较重要的问题.前面在铁基母体材料中所得到的电子向列相是从FT-QPI实验中发现的,而FeSe材料中测量的FTQPI图案也有很明显的二度对称性,如图14(a)和图14(b)所示,而且随着能量从正能到负能的改变,强度分布好像旋转了90◦.最近的研究表明,上述二度对称的FT-QPI图像,主要来源于FeSe中严重拉长的电子/空穴费米口袋结构[59].因为FT-QPI图案是q空间的信息,FeSe电子或者空穴口袋袋内散射,都会集中在中心斑纹处.测量得到的中心斑纹,由不同费米面的色散关系,在正能测量时电子口袋内的散射的确应该占主要部分,而在负能测量时空穴口袋内的散射应该占主要部分.另外结合yz轨道比xy和xz轨道有着更大的态密度权重,可以基于费米面的结构解释上述二度对称的FT-QPI图案,而不需要额外的电子向列相[59].因此,二度对称的FT-QPI图案并非主要来源于电子的向列相,而是主要来自于二度对称的费米口袋.而电子态的各向异性在FeSe厚膜中却有所体现,包括图14(c)中显示的由Se杂质产生的间距为16aFe-Fe的电子态的周期结构和图14(d)中显示拉长的磁通图像.虽然后者可能是由各向异性的能隙造成的,与图8(d)所示二度性的能隙对应,但是其拉长的方向和晶格方向相同,也验证了电子态存在着各向异性.需要注意的是,FeSe单晶中不存在长程磁有序,低温下形成的正交电子向列相会直接影响超导相,因此对FeSe超导电性的研究有着重要的意义. 图14 FeSe中可能的电子向列相 (a),(b)不同能量测量的FeSe单晶的FT-QPI图案[59];(c),(d)FeSe厚膜上Se杂质附近实空间的电子波调制和磁通图像[39]Fig.14.Possible nematicity in FeSe:(a),(b)FT-QPI patterns obtained at dif f erent energies[59];(c),(d)possible nematic electronic nanostructure near a Se adatom and elongated vortex image in FeSe thick f i lm[39]. 对于普通超导材料,能带在零能附近打开一个超导能隙∆,通常材料能带的费米能EF(eV量级)比超导能隙(meV量级)大得多.铁基超导体是一个典型的多带多能隙超导体,部分或者全部能带的费米能EF非常小(几十或者上百meV),在此情况下,超导能隙(几个到十几个meV)和费米能的比值∆/EF较普通BCS超导体的来说大很多.浅能带现象在FeSe和Fe(Se1−xTex)材料中更明显.STM实验中,可以通过测量不同能量的FT-QPI图案得到能带色散的信息,虽然无法得到各能带在动量空间的具体位置,但能得到能带的电子空穴属性和费米能的大小.图15(a)和图15(b)显示了FeSe单晶在12 T高场下测量的不同能量的FT-QPI强度组合得到的能量色散结果[40].因为该材料的费米能非常小,所以需要高场破坏超导能隙来得到清晰的能带信息.这样的结果和ARPES测量的能带色散图看上去类似,但是其中横轴的量是q,不代表能带在动量空间k的具体位置.图15(a)给出的是空穴型能带色散,其费米能(价带顶的能量)大概在10 meV;图15(b)给出的是电子型能带色散,其费米能(导带底的能量)大概只有3 meV.对比到该材料中2.5—3.5 meV的超导能隙可以发现,FeSe确实是一个能带特别浅的材料. 当费米能非常小时,材料可能更容易满足量子极限(T/Tc≪ ∆/EF),那么就有可能观测到1964年理论预测的能量分立的磁通束缚态(Carolide Gennes-Matricon state,CdGM state)[60,61].在0.48 K温度和较高的4 T磁场下,使用STM针尖在FeSe0.45Te0.55磁通中心观测到了CdGM态中的三个束缚态能级[62],如图15(c)和图15(d)所示.这三个峰对应的能量大约是0.45,1.20和1.90 meV,其比值是1:2.7:4.2,与理论上预言的CdGM态的一级,二级和三级能量比值很接近.此外,这些峰能量基本不随测量位置的变化而变化,进一步验证了它们是分立的磁通束缚态.考虑到CdGM能级能量Eµ= ±µ∆2/EF(µ =1/2,3/2,5/2,···),以及超导能隙范围在1.1—2.1 meV,能够计算出费米能的范围约为1.3—4.9 meV,和角分辨光电子谱得到的结果类似[63],进一步验证了材料的浅带效应. 可以发现,FeSe和Fe(Se1−xTex)材料中,超导能隙和费米能的比值大概为1/5<∆/EF<1,这个比值非常大.换另一个角度量化这个问题,BCS超导体中普通超导体的超导临界温度和费米温度之比Tc/TF仅为10−5—10−4,而FeSe中只有0.2,这个数值甚至大于铜氧化物的数值,可能证明了材料靠近玻色-爱因斯坦凝聚(Bose-Einstein condensate,BEC)型的强涨落超导体[40,64].根据简单的理论推导,比值TF/Tc大约对应于单位相干长度ξ内存在的库珀对的数目.在BCS图像下,在相干长度或相干体积内,数万个库珀对纠缠在一起,无法从实空间分辨出来.然而在BEC图像下,相干长度范围内的库珀对将非常少,甚至只有一对,被认为是实空间配对,因此对应的超导电性和BCS超导体比将有非常大的区别.FeSe和Fe(Se1−xTex)材料可能只是处于BCS的BCS-BEC过渡态,因此可能还没有BEC超导体那么明显的超导涨落[65].而且铁基超导体具有多能带特性,作为其中的一条或者几条能带,浅带在里面的作用还需要进一步详细探讨. 图15 FeSe基材料中的浅能带行为 (a),(b)由高场12 T下FeSe单晶的FT-QPI推得的能带色散关系图[40];(c),(d)磁场4 T下测量的FeSe0.45Te0.55单晶磁通中心的磁通束缚态[62]Fig.15.Shallow band properties in FeSe-based superconductors:(a),(b)Band dispersions deduced from the FT-QPI pattern in FeSe measured at high magnetic f i eld of 12 T[40];(c),(d)vortex bound state peaks observed at the vortex core center in FeSe0.45Te0.55at a magnetic f i eld as high as 4 T[62]. 拓扑超导是凝聚态物理中的前沿领域之一.理论预测拓扑超导具有奇宇称超导序参量,可能出现Majorana费米子,并在量子计算中有潜在应用前景[66,67],这使其备受关注.在拓扑超导中,磁通中心将会出现理论预言的Majorana零能模[66,67].因为拓扑超导很难寻找,通常用超导邻近效应来诱导,如在s波超导体上生长拓扑绝缘体薄膜诱导出超导来尝试实现,而磁通芯子中的Majorana零能模就首先在Bi2Te3/NbSe2异质结上被观测到[68].最近,在掺杂的拓扑绝缘体材料CuxBi2Se3中也观测到了可能的Majorana零能模峰[69].在拓扑半金属Cd3As2表面,使用针尖诱导的超导中,也观测到了可能的Majorana零压电导峰[70].在铁基超导体FeSe单层薄膜上,利用分子束外延生长技术沉积Fe原子,在Fe原子上也观测到了可能的零能模,这一零能模对应的超导Tc更高,而且不需要外加磁场诱导[71]. 同时,铁基超导体本身与拓扑的关联也已“悄然”建立.在FeSe1−xTex材料中,由于布里渊区Γ点附近的pz和dxz/dyz轨道间的强自旋轨道耦合并导致能带反转,被理论预言[72,73]具有可能的拓扑表面态,而且利用自旋分辩的ARPES发现在该材料中存在自旋螺旋型的Dirac表面态[74].进一步的STM实验在小磁场下在该材料磁通中发现了可能的Majorana零能模[75].图16(a)是在0.5 T较小磁场和0.55 K较低温度下测量得到的FeSe0.45Te0.55的磁通芯子图像,图16(b)和图16(c)是一系列过磁通中心测量的隧道谱.可看到在磁通中心点测量的隧道谱有着尖锐的零能峰,在空间延展而不劈裂也不移动.实验中还在该磁场下发现第一级CdGM磁通束缚态峰,其能量大概在0.7 meV,和观测到的零能峰可以区别开.作者认为该实验结果表明磁通中心存在着Majorana零能模. 最近在另一个FeSe插层材料(LixFe1−x)OHFeSe厚膜中,也观察到可能的Majorana零能模[76].利用ARPES在该材料的Γ点附近也发现了Dirac型线性色散的表面态和Dirac点.通过STM测量得到的磁通束缚态,在其中发现零能有个明显的峰,且不随空间位置的变化而劈裂或移动.除了零能模以外,在正负能各有几个非零能的峰.作者认为它们分别来源于表面p波超导磁通束缚态(0级即为Majorana零能模)和体s波超导普通CdGM磁通束缚态[76]. 上述两种铁基超导材料磁通中发现的零能模是否是Majorana零能模,以及是否就说明出现了拓扑超导,还需要进一步的实验验证.如果证实,那么铁基超导体可能是一个“天然”的拓扑超导体,这为操纵Majorana费米子并最终实现容错量子计算提供了一个新的平台. 图16 FeSe0.45Te0.55磁通芯子中观测到的Majorana零能模[75]Fig.16.Majorana zero-energy mode observed in the vortex core in FeSe0.45Te0.55[75] 近十年来,关于铁基超导体的STM研究取得了一系列重要进展,本文在铁基超导机理和其中的奇异电子态方面进行了简要总结.但是需要注意的是,铁基超导体是一个多带多能隙系统,不同材料的费米面有很大的区别,另外还有各种有序态相互竞争或合作,呈现出纷繁复杂的物理现象.目前得到基本一致的认识是超导与反铁磁涨落密切相关,但是电子配对是强耦合情况下的局域配对还是弱耦合情况下的延时配对仍然没有定论.铁基超导体表现出来的浅能带效应、多种有序相的竞争和合作,也许是理解其非常规超导机理的关键,而扫描隧道显微镜实验将会发挥重要作用. 由于在铁基超导体上进行扫描隧道显微镜研究的小组很多,结果也极其丰富,我们这篇短文不可能作全面概括.如果有优秀工作没有被概括进来,敬请原谅.
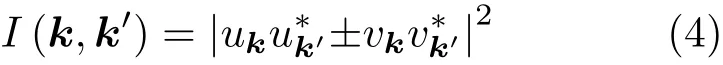

3 STM对铁基超导体能隙的研究
3.1 铁基超导体配对对称性简介
3.2 有空穴和电子费米面的铁基超导体s±配对的STM证明

3.3 相位敏感的QPI技术及其理论分析
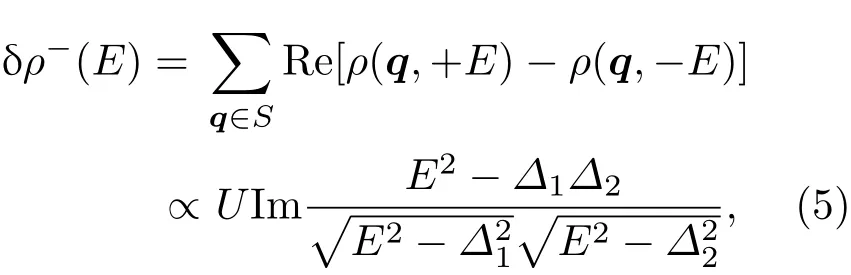



3.4 FeSe单晶超导体配对对称性
3.5 空穴费米口袋缺失的FeSe基超导材料的配对对称性研究

4 铁基超导体中奇异电子态的STM研究
4.1 电子向列态

4.2 铁基超导中的浅能带效应

4.3 铁基超导体中可能的Majorana零能模的发现

5 结论与展望
