基于调制光晶格的中性分子束光学Stark减速与囚禁的理论研究∗
2018-11-28李晓云孙博文许正倩陈静尹亚玲印建平
李晓云 孙博文 许正倩 陈静 尹亚玲 印建平
(华东师范大学物理与材料科学学院,精密光谱科学与技术国家重点实验室,上海 200241)
本文基于分子束光学Stark减速理论,提出采用调制的红失谐光晶格来减速和囚禁任意脉冲超声分子束方案,并予以理论研究.以CH4超声分子束为例,利用Monte-Carlo方法模拟了调制光晶格中的分子减速与囚禁的动力学过程,给出减速级数、同步分子初始位相角与减速效果的关系.研究结果表明:随着减速级数的增加,被减速的分子波包逐渐从原来的分子速度分布的大波包中分离开来,且减速级数越高,减速后的分子速度越小.在其他条件相同时同步分子初始位相角越大,减速波包内的分子数目越少,同时位相空间被压缩.与未调制的光晶格减速方案相比,本方案中无分子自由飞行过程,在相同的光晶格长度内完成了双倍的减速级数.当光晶格长度取3.71 mm时,模拟结果显示CH4分子从280 m/s减速至172 m/s,而未调制光晶格只能将CH4分子从280 m/s减速至232 m/s,减速效果提高了26%.本方案可以集分子的减速、囚禁于一体,是一种新型的分子光学功能器件,在冷分子光学、量子信息、冷化学等前沿研究领域中有潜在的应用.
1 引 言
分子冷却对于分子光学、超冷分子物理以及分子玻色-爱因斯坦凝聚态的制备等相关研究至关重要,为凝聚态物质以及量子信息物理的研究提供了实验基础.在该背景之下,气相冷分子成为科学家们在掌握了基本操控方法后的一个热点研究对象.冷分子丰富的内态能级结构使得它在基本物理问题和物理常数的精密测量、分子冷碰撞和冷化学、冷分子光谱学、量子信息和量子计算等领域有着重要的潜在应用[1−3].
目前,科学家们采用非均匀静电场[4−8]、非均匀静磁场[9−11]以及非均匀微波场[12,13]已成功实现了脉冲超声分子束的减速,并得到了温度在mK量级的慢速分子.然而,静电场只能操控极性分子,而静磁场只能操控顺磁性分子,也就是说这些技术的应用范围是有限的.但是,不管是极性分子还是非极性分子,顺磁性分子还是非顺磁性分子,它们都能够在强光场中感应出电偶极矩,从而具有二阶势能.因此,当分子在非共振的激光场中运动时,将受到光场的电偶极相互作用.即当分子在光场中运动时,若光场偶极力的方向与分子运动方向相同,则分子被加速.若光场偶极力的方向与分子运动方向相反,则分子被减速.2004年,英国Barker小组在实验上实现了脉冲分子束的单级光学减速,在15 ns的时间内用单个脉冲高斯光场将苯分子束的平动动能减小了15%[14],在实验过程中通过时序控制系统控制脉冲阀的打开时间与激光器的打开时间间隔来控制光场打开时分子在光场中的位置,从而实现分子的减速,并于2006年在实验上成功实现了基于激光光晶格的NO分子的单级加速或减速[15];同年,美国Chandler小组在实验上运用相似的思想,在具体实验中通过调节光晶格的强度来控制光晶格减速与加速分子束的程度[16].2009年,华东师范大学印建平小组[17]提出了一种新颖的用于减速脉冲超声分子束的多级光学Stark减速器,这是一种采用静止的红失谐准连续光学晶格来减速与囚禁脉冲超声分子束的方案,成功模拟了CH4分子在多级光晶格光场的作用下分子束中心速度的有效减速.2012年,该小组又提出了一种运动的光学晶格实现脉冲亚超声分子束的多级光学Stark减速的方案[18].在本文中,我们针对利用静止的红失谐准连续光晶格来减速与囚禁脉冲超声分子束的方案提出了一种新的改进方案,即利用调制的光晶格代替静止的光晶格,在相同长度的光晶格内,获得双倍的减速级数,从而获得更好的减速效果及更多数目的冷分子.
2 调制光晶格减速并囚禁超声分子束的基本原理
我们采用调制的红失谐光晶格减速并囚禁超声分子束,具体原理如图1所示,由两束近似于反平行的高斯激光束构成一维静止的光学晶格,两束激光之间的夹角为β.在两束激光的重叠部分激光相干叠加,从而形成周期性光场分布,即驻波场光晶格.当一束脉冲超声分子束沿着z方向传播并通过光晶格的中心部分时,在光晶格周期性的势场中该束分子将受到光学偶极力的作用,分子的速度及位置在光场的作用下发生改变.通过对光晶格势场空间分布的时序调控来实现对分子在晶格中运动状况的控制,进而使超声分子束中的部分分子在光学晶格中进行持续减速运动,最终沿z方向输出.

图1 准连续光学晶格减速与囚禁脉冲超声分子束原理图,MB为入射分子束,LB1和LB2为激光束Fig.1.The schematic diagram of multistage optical deceleration and trap for a supersonic molecular beam using quasi continuous optical lattice,here MB is the incident molecular beam,LB1 and LB2 are laser beams.
构成光学晶格的两束激光LB1和LB2波长均为λ,夹角β约为175◦,由光晶格理论可以得知光晶格的空间周期Λ≈λ/2,且由于两束激光的波长相同,可以构成稳定的光晶格.一维驻波光晶格在z方向的光场强度可表示为()
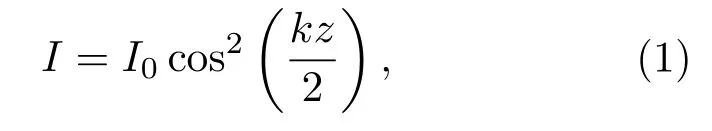
其中I0表示光晶格光场强度的幅值,k =[4πsin(β/2)]/λ表示光晶格的波数. 同时,光晶格的频率相比大多数分子的电子跃迁能级是超大红失谐的.根据交流Stark效应,处于红失谐的一维驻波光晶格中的分子具有的光(学偶)极势为
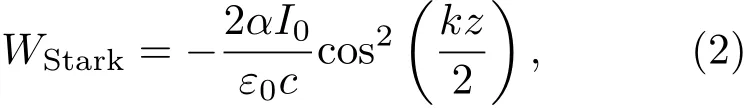
其中α表示分子的平均极化率,ε0表示自由空间的极化率,c是真空中的光速.
根据(2)式,以及偶极力与光学偶极势之间的关系,可以得到分子在z方向运动时所受到的光晶格的光场偶极力的表达式为

由(3)式可以看出该偶极力与晶格光场强度I的梯度成正比关系.所以,处于晶格中的分子的经典牛顿运动方程可以写为

其中m表示分子的质量.
根据(2)式,可以绘出处于光晶格中的分子所具有的周期性光学势曲线图,如图2(a)所示.从图中能够明显看出分子所受到的偶极光学势的周期与光晶格的空间周期相同,且分子的光学势大小与分子所处光晶格的具体位置有着密切关系.为了便于描述,引入位相角φ,定义φ=(z/Λ)×360◦,周期为360◦,从而将分子的空间位置转换为角度.在图2(a)中,当位相角0◦< φ<180◦时,随着分子在光场中的位相角不断增加,其光学势能也在不断增加.根据能量守恒定律可知,当分子的势能增加时,动能则在不断减小,分子从而被减速.当位相角180◦<φ<360◦时,随着在光场中的位相角的不断增加,其光学势能在不断减少,由能量守恒定律可知其动能在不断增加,分子从而被加速.对此,我们也可以采用(3)式进行解释,当位相角0◦<φ<180◦时,分子所受到的光场偶极力方向为z轴负方向,与分子的运动方向相反,所以分子进行减速运动.而当位相角180◦<φ<360◦时,分子受到的偶极力方向与分子运动方向相同,所以分子进行加速运动.在光晶格的一个周期范围内,分子在一半的周期范围内被减速,在另一半的周期范围内被加速.
为了更有效地利用光晶格实现分子减速,可以借助于光学方法调制光晶格的空间分布.分子在调制后的光晶格中的光学势如图2(b)所示,分子在势能曲线上不断爬坡,此过程分子速度不断减少.当分子到达势能顶点时,调制光晶格,使分子获得与前半个周期相同的势能分布,分子继续爬坡,从而实现一个周期内的两次减速.再重复上述过程,这样通过分子与调制光学晶格的多次相互作用,就可实现脉冲分子束的不断减速.该方案光晶格被充分利用,分子在光晶格中运动的过程中无自由飞行,从而降低分子束的横向扩散.关于光晶格的调制,在实验上并不难实现,可以利用压电陶瓷的静态特性调制激光场,配合分子束运动的时序,保证分子一直处于爬坡区间.压电陶瓷具有一定的响应时间,对光场调制有滞后,从而会影响减速效果.为此在设计光场调制时序时可将该压电陶瓷的响应时间考虑进去,从而达到实验设计预期,获得较好的减速效果.
由于超声分子束具有一定的速度分布以及空间位置分布,因此对于每一个分子来说,相应的光场时序是完全不一样的.但是减速方案是采用一套时序来控制某一速度群分子的运动,也就是说我们不能满足分子束中所有分子的同步要求,或者说只能使一部分分子的步调与光场的步调一致,从而实现减速,而其他的分子或被加速或保持不变.因此,选择分子束中具有某一速度的分子作为同步分子来调制光晶格.同步分子从光晶格的波腹处开始运动,也就是分子的位相为φ=0◦.分子在光场的作用下势能不断增加,一旦分子到达φ=φ0(该角度定义为同步分子位相角)的位置,调制光晶格,使分子在光晶格中的势能曲线移动,与φ=0◦时的势能曲线相同.分子则继续爬坡,使分子始终处于减速区.之后不断重复这个过程,同步分子在每一级的减速中损失相同的动能.在光晶格被调制后,分子将失去一部分势能,这部分势能由调制的光场带走,此原理与分子的静电Stark减速类似[4−8].其他分子的动能变化情况由光场调制前后它们本身的位置和速度决定.此外,红失谐的光晶格也是周期性光学势阱,分子可以被囚禁在光晶格的波腹处,则本方案可以同时实现分子的减速与囚禁.
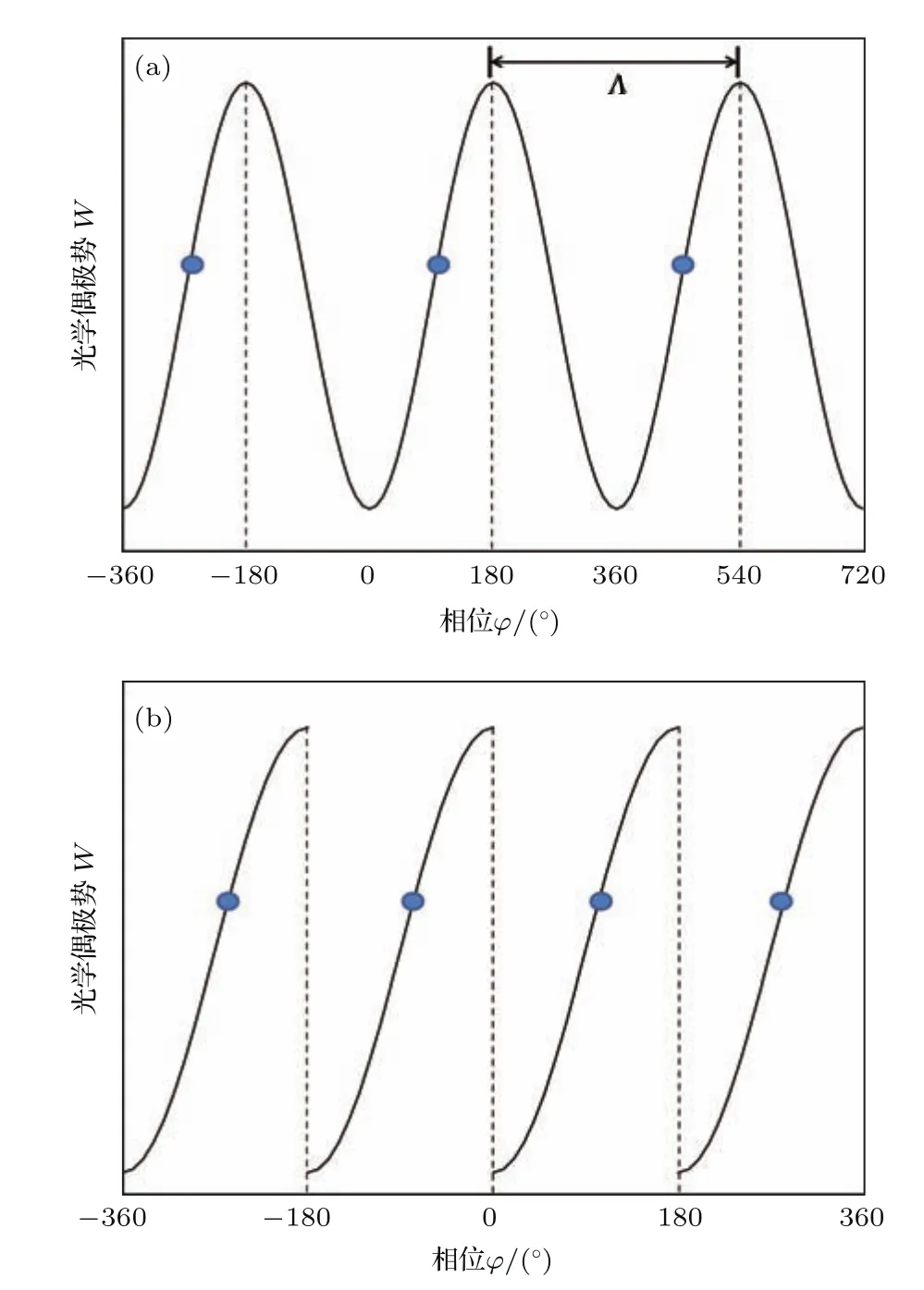
图2 分子的周期性光学势分布图 (a)处于光晶格中;(b)处于调制光晶格中Fig.2. Periodic optical potential distribution of molecules:(a)In optical lattices;(b)in modulated optical lattices.
3 Monte-Carlo模拟结果分析与讨论
为了验证该理论方案的有效性,我们利用Monte-Carlo方法模拟超声分子束在光晶格中运动的动力学过程.选择束流中心速度u=280 m/s,纵向平动温度为1 K的甲烷(CH4)超声分子束[4].超声分子束纵向速度分布为
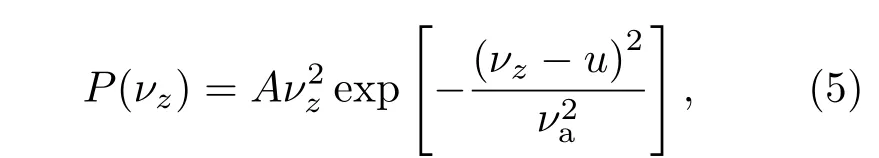
同时,同步分子周围一定范围内的分子将会与同步分子一起慢慢减速,这些分子的具体数目与光场的参数有关.设置同步分子的初始速度为v0,同步分子位相为φ0,光场减速的级数为n,根据前面的分析以及(2)式,得到同步分子在n级减速之后的速度为
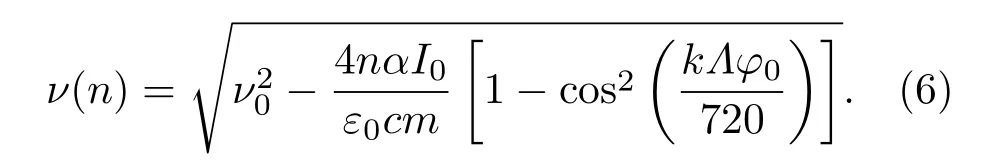
由(6)式可以看出,同步分子的最终速度与同步位相角φ0以及减速级数n都有关系.接下来分别研究在初速度v0相同的情况下,分子减速与减速级数n以及同步位相角φ0之间的关系.
3.1 减速效果与减速级数n的关系
在讨论脉冲分子束的光晶格减速时,光场调制时序设定为当光晶格开始调制时,同步分子在每一级的减速中都处于相同的位置,那么分子在每一级的减速中损失的动能相同.设置φ0=90◦,ν0=280 m/s,模拟的减速分子的时间飞行(TOF)信号如图3所示.图中横坐标是分子从与光场相互作用的开始位置运动到探测位置z=d=0.007 m=7 mm时所需要的时间,纵坐标是分子数占整个分子束分子总数的比例,即相对分子数.图3中四条曲线分别是当减速级数n=0,n=10000,n=14000,n=18000时分子束与光场相互作用后的TOF信号,它是分子位置和速度共同作用的结果.很明显,除了第一条曲线n=0,无减速波包外,其余三条曲线均出现了两个波包,小的波包均在大的波包的右边,它对应的飞行时间长,表示该处是被光场减速的分子.这些分子已从原来的分子速度分布中分离出来,而且随着减速级数的增加,小的波包离大波包越来越远,减速后的分子速度也就越来越低.当n=10000时,同步分子的速度从280 m/s降低到209 m/s;当n=14000时,同步分子的速度从280 m/s降低到173 m/s;当n=18000时,同步分子的速度从280 m/s降低到123 m/s,速度已经小于初始速度的一半.如果我们继续增加减速级数,那么分子的速度还会继续降低,甚至速度被降为零或反向.当减速级数继续增加时,减速波包的峰值强度降低了,但是波包分布宽度变宽了,减速波包内分子数目不变.经过统计,减速波包内的分子数目约占入射分子束中分子总数的2.5%.
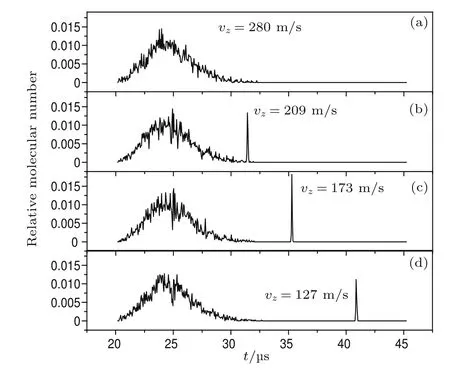
图3 当同步分子的位相φ0=90◦时,不同光场减速级数n时分子束与光场作用后的TOF信号图 (a)n=0;(b)n=10000;(c)n=14000;(d)n=18000Fig.3.Simulated time-of-f l ight signal of molecules after the action of the molecular beam and the light f i eld for the various deceleration stages with the same synchronous phase angle φ0=90◦:(a)n=0;(b)n=10000;(c)n=14000;(d)n=18000.
3.2 减速效果与同步分子初始位相角φ0的关系
不同减速级数条件下,减速波包内分子的位相空间演化,结果如图4所示.同步分子的位相φ0=90◦,光场减速级数分别为n=10000,n=14000,n=18000.横坐标是分子的空间位置z,纵坐标即分子在z方向上的速度.很明显,减速分子的位相空间随着减速级数的增加在不断地扭曲,但是位相空间的面积几乎不变,这是因为同步分子的位相始终保持φ0=90◦不变.这说明减速分子波包内的分子随着同步分子一级级往下减速的同时,它们就在同步分子周围振荡.
由之前的研究结果可知,通过改变同步分子的不同位相角,可改变分子在每一级减速过程中所损失的动能,同时位相稳定区域的面积也发生改变[4].设定分子的光场减速级数n=14000保持不变,v0=280 m/s,分别模拟同步分子的位相角φ0=70◦,φ0=90◦,φ0=105◦,φ0=120◦时分子束与光场作用后的TOF信号,相应结果如图5所示.在模拟过程中激光和分子束的其他参数均与图3相同.很明显,图5中4条曲线均存在两个波包.随着位相角的增加,减速波包离大波包距离增加,说明减速分子的速度越低.同时可以观察到随着位相角的增加,波包的分子数目降低了,这说明位相稳定区域的面积降低了.这是由于同步分子的位相角越大,分子在每一级损失的动能也就越大,减速效果也就越好.但是减速波包里的分子数目降低,所以具体实验时要权衡选择同步位相角.
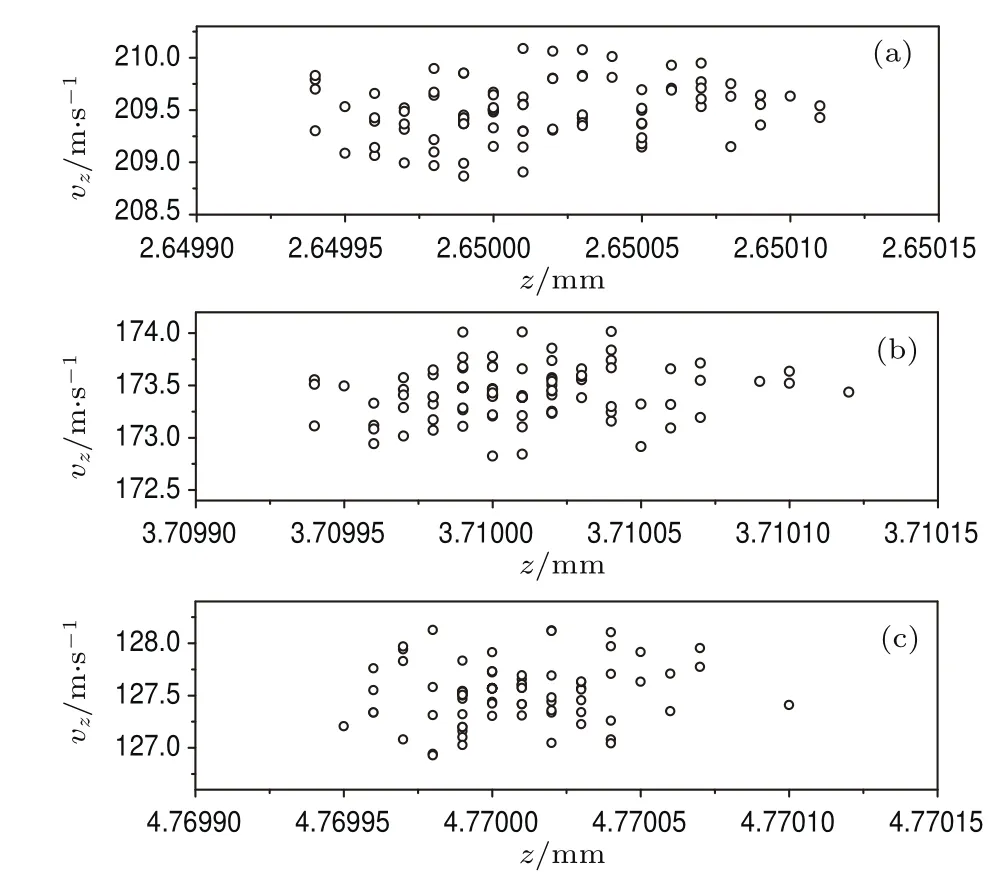
图4 当同步分子的位相φ0=90◦时,不同光场减速级数时,与光场作用后减速分子波包的位相空间演化 (a)n=10000;(b)n=14000;(c)n=18000Fig.4.Simulated phase-space plot of the slowed molecular packet for the same synchronous phase angle φ0=90◦ and dif f erent deceleration stages:(a)n=10000;(b)n=14000;(c)n=18000.

图5 当光场减速级数n=14000时,不同相位时CH4分子与光场作用后的TOF信号图 (a)φ0=70◦;(b)φ0=90◦;(c)φ0=105◦;(d)φ0=120◦Fig.5. Simulated TOF signal of CH4molecules at the outlet of the decelerator for the deceleration stages n=14000 and dif f erent synchronous phase angle:(a) φ0=70◦;(b) φ0=90◦;(c) φ0=105◦;(d) φ0=120◦.
为了更好地描述减速分子波包随着同步位相角的变化,用位相图将减速分子的坐标以及速度展现出来,如图6所示.令光场减速级数n=14000保持不变,位相角分别取φ0=70◦,φ0=90◦和φ0=105◦.由图中可以看出减速波包内的分子随着位相角φ0衍化,为了更好地比较,在绘图时选取同一横坐标,表示不同位相角分子在光晶格中被测量的空间位置相同;速度分布间隔相同的纵坐标,表示被减速后的同步分子的速度.很明显,同步分子的位相角φ0越大,同步分子的速度越低,位相空间的面积越小,速度空间的分布宽度越窄,空间位置的分布宽度也越窄,处于减速波包内的分子数目也越少.同样减速波包内分子的空间位置和速度均在同步分子周围振荡.

图6 光场减速级数n=14000时,不同相位与光场作用后分子减速波包的位相空间衍化图 (a)φ0=70◦;(b) φ0=90◦;(c) φ0=105◦Fig.6. Simulated phase-space plot of the slowed molecular packet for the deceleration stages n=14000 and dif f erent synchronous phase angle:(a) φ0=70◦;(b) φ0=90◦;(c) φ0=105◦.
3.3 相同长度的调制光晶格与静止的准连续光晶格减速效果的比较
本文提出的基于调制光晶格的方案与之前的准连续光晶格减速脉冲分子束的方案相比,主要区别在于是否在减速过程中移动光晶格.现将新的减速方案与之前的方案在减速超声分子束方面做一个详细的比较.选择与原始方案完全相同的分子束参数,晶格参数的选择也与上述模拟时采用的参数完全相同,同步分子的位相角为φ0=90◦,超声分子束初始束流速度u=280 m/s,模拟5×105个分子的减速.当取相同的光晶格长度,即L=3.71 mm时,利用Monte-Carlo法分别模拟了两种情况下CH4分子束的减速,得到的减速后的TOF信号图如图7所示.
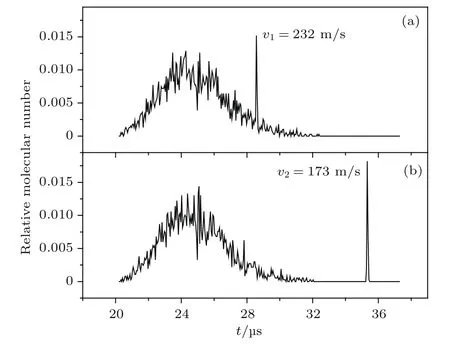
图7 原方案与改进方案减速效果图 (a)原方案;(b)现方案Fig.7.The deceleration ef f ect diagram of the original scheme and the improvement plan:(a)The original scheme;(b)the present scheme.
从图7中可以明显地看出,当光晶格长度相同时,改进方案的减速波包比原方案的减速波包离大波包更远,也就是说现在的速度被减至更低,分子从280 m/s被减速至173 m/s,而原方案的分子被减速至232 m/s,通过比较可知本方案减速效果更好.同时,分子波包内的数目也相较而言有所提高.这是由于本方案在相同的光晶格长度内,完成了双倍的减速级数,即在原方案完成7000级减速的同时,本方案完成14000级减速,同时避免了分子的自由飞行,因此在减速效果提升的同时也减少了分子数的损失.
4 总 结
本文在准连续光学晶格Stark减速分子方案的基础上,提出了一种调制的光晶格减速超声分子束的方案.它能够在相同的光晶格长度下,提高分子束的减速效果,同时被减速的分子数目也有所提高,新的减速方案实现了更高效的中性分子束光学Stark减速与囚禁.以CH4超声分子束为例,本文利用Monte-Carlo方法模拟了调制光晶格中分子减速与囚禁的动力学过程,讨论了减速效果与减速级数n以及相位角φ0的关系.由模拟结果可知,减速的级数n越多,位相角φ0越大,减速后的分子速度越小,但是减速波包内的分子数目也越少.本方案可以作为冷分子的制备方法,为冷分子的应用提供冷分子源[19−22].本方案可以集分子的减速制备、囚禁于一体,是新型的分子光学器件,在冷分子光学、量子信息、冷化学等前沿研究领域中有潜在的应用.
