改进的量子粒子群优化算法对多维多选择背包问题的求解

杨 雪, 董红斌, 董宇欣

(哈尔滨工程大学 计算机科学与技术学院, 哈尔滨 150001)

多维多选择背包(multi-choice knapsack problem, MMKP)是0-1背包的一种变体. 在MMKP问题中, 一些同时占有多种类型资源的物品被分成不同组, 这些物品对应不同的价值. 在每组内选择一个物品放入背包, 使得在满足所有资源限制条件下背包的总价值最小. 这种对不同物品和资源的组合利用使得多维多选择背包问题应用广泛, 如关键字拍卖、 路径规划、 传感器网络配置等. MMKP是典型的NP难问题, 即使只对二维问题也不存在多项式时间解(polynomial-time approximation scheme, EPTAS), 除非P=NP. 对于MMKP问题通常有两种求解思路： 直接求解或启发式算法求解. 直接求解旨在求解目标问题的精确全局最优值[1-3]. 但由于MMKP问题是一种基于约束限制的NP难问题, 所以通常采用启发式算法, 以便在可行时间内获得可接受的近似最优解, 但由于MMKP问题的可行域分散, 启发式算法易陷入局部最优解.

文献[4]提出了使用两种近似算法求解多维多选择背包问题： 第一种是简单应用局部搜索的方法； 第二种使用了一个记忆列表替代原局部搜索策略. 虽然第二种方法的运行速度较慢, 但实际求解结果远好于第一种方法, 在多数情况下都能找到全局最优值. Htiouech等[5]提出了一种代理信息作为选择规则的启发式方法, 该方法是从可行域的两侧进行搜索, 并使用一种约束规范化的方法加强约束. 该方法在有限时间内求解的精度较高. 在群智能算法求解多选择背包问题上, 文献[6]提出了两种新的蚁群克隆算法进行求解, 通过增加随机局部搜索, 提高局部搜索能力和收敛速度.

在求解背包问题时如何保证种群的多样性是算法设计的关键. 演化算法的提出为多项式时间内求解约束优化问题提供了一种新途径. 粒子群算法(PSO)是对鸟类行为模拟基础上提出的一种解空间搜索算法[7-8], 由于其参数少、 易控制、 收敛速度快等优点被广泛应用. 但粒子群算法被证明不能保证收敛到全局最优解[9]. Sun等[10]提出的量子粒子群优化算法(QPSO), 将粒子群中的粒子视为具有动量和能量的粒子, 用波函数表示其运动状态, 通过Monte Carlo测定方法确定粒子的最终位置, 提高了粒子群算法的全局搜索能力[11-12]. 由于QPSO算法高效的全局搜索能力, 在图像处理[13]和聚类[14]等领域中应用广泛.

1 预备知识

1.1 多维多选择背包问题

多维多选择背包问题是指存在一些物品, 这些物品被分成l种不同的类, 第i类有li个物品. 每个物品有一定的价值σi, 并占用m种不同类的资源, 则第i类中第j个物品所占用的资源可用向量rij=(rij1,rij2,…,rijm)表示. 从每类中选择至多一个物品放入背包中, 使背包中的物品所占用的资源数小于可提供的总资源数b=(b1,b2,…,bm), 并使背包内物品的总价值最高. 多维多选择背包问题可以形式化地描述为

(1)

其中σij表示第i类中第j个物品的价值.

1.2 QPSO算法

PSO算法的形式化描述为： 在一个N维的搜索空间中有k个粒子, 第i个个体的属性由两个向量组成(xi,vi), 其中向量xi=(xi1,xi2,…,xin)表示粒子i目前所处的位置; 向量vi=(vi1,vi2,…,vin)表示粒子的速度. 对于第i个粒子, 还记忆两个共享值： 该粒子搜索到的最优位置pi={pi1,pi2,…,pin}和整个种群搜索到的最优位置pgd.

粒子群优化算法步骤如下：

1) 在N维解空间内初始化m个粒子.

2) 对种群内所有的粒子根据

(2)

3) 计算种群的适应度.

4) 更新粒子历史最优位置和全局历史最优位置.

5) 判断种群是否符合终止条件, 符合则算法结束, 否则转2).

由于传统粒子群优化算法存在收敛过快等问题, 所以提出了量子粒子群优化算法. 在量子粒子群优化算法中, 假设粒子群系统是一个量子粒子系统, 每个粒子具有量子行为状态, 用波函数Ψ(X,t)描述, 其物理意义是： 波函数模的平方是粒子空间某一点出现的概率密度. 在确定了粒子的分布概率密度后, 根据Monte Carlo随机模拟的方式测定粒子位置. 与粒子群优化算法不同, 量子粒子群优化算法通过下列公式进行参数更新：

pij(t)=φj(t)·pij(t)+(1-φj(t))·Gj(t)，φj(t)～U(0,1)，

(3)

(5)

其中:φ,β,u是[0,1]内的随机数;Pi是粒子i的个体最好位置. 在量子粒子群优化算法中, 只有α为唯一的控制参数, 称为收缩扩张(contraction-expansion, CE)系数. 文献[10]研究表明,α<1.781是算法单个粒子有界性的充要条件.

2 精英保留协同量子粒子群优化算法

图1 一个二维最大值寻优问题Fig.1 Two-dimensional maximum optimization problem

多维多选择背包问题的强约束性质导致标准量子粒子群优化算法易陷入局部最优值, 特别是对于高维问题, 可行域被分成多个离散空间, 使得启发式算法易局部收敛. 在标准量子粒子群中, 粒子在产生下一代个体时, 没有经过选择过程而是根据全局最优解和粒子历史最优位置而产生的中心吸引点, 在该吸引点附近进行扩张. 但在粒子的进化过程中, 父代个体中较好的基因可能被丢弃, 会损失部分种群多样性, 算法的优化过程将持续在局部最优解附近搜索. 因此, 如何衡量每个粒子的有效性并增加种群多样性是提高QPSO算法对MMKP求解的关键. 基于此, 本文提出一种新的协同进化框架, 当主进化种群内的个体种群多样性降低时, 在保留了进化历史上优质基因个体的副种群中选择个体对主种群中的个体进行变异.

2.1 基于位置信息的粒子可用性度量

为分析粒子群优化算法中的种群多样性, 首先分析一个简单的二维最大值寻优问题： 设在连续问题中Δx为一个无穷小量, 在离散问题中Δx为自变量改变的最小步长,x(t)是第t代的一个个体,x(t+1)是该个体的子代个体,f(x)是问题的适应度函数, 则一个二维问题可表示为如图1所示.

同理, 当x(t+1)向x(t)增加一个小的增量Δx(此时Δx为负值)时, 也可获得与上述定义相同的3种运动趋势. 根据父代个体与子代个体形成的6种不同运动趋势, 粒子与子代个体中可能的运动情形如图2所示.

定义2(吸引运动) 当两个个体相互之间有趋向运动, 即a→b且b→a时, 称两个个体相互吸引, 记为Att(a,b), 如图2(A)所示.

定义5(无指导运动) 当父代个体a或子代个体b无运动趋势时, 即a∝b或b∝a时, 称为无指导运动, 记为No-m(a,b), 如图2(D),(E),(F)所示.

图2 粒子运动趋势Fig.2 Moving trends between particles

由图2可见: 当父代个体与子代个体进行吸引运动、 追逐运动和无指导运动时, 两个个体趋向于在同一个峰值上共同寻优, 所以进行选择时仅保留适应度最大的个体即可保留种群的多样性; 当父代个体与子代个体进行排斥运动时, 父代个体与子代个体可能在不同峰值上寻优, 则需要同时保留父代个体与子代个体, 将父代个体保留至副种群中, 保留基因的多样性. 同理, 粒子的运动也可以推广到多维空间.

2.2 位置扰动

在量子粒子群优化算法中, 中心吸引子的位置在历史最优位置和全局最优位置的联合作用下产生, 随着迭代次数的增加, 新的粒子将会随着种群的多样性增加移动到相同位置. 为了避免这种现象, 在QPSO算法中加入位置扰动.

首先, 当进化种群的多样性低于阈值时, 从副种群中随机选择个体对主进化种群中的最优个体基因进行替换. 本文选取按照位置重心的方法计算种群多样性, 定义如下：

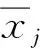
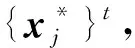
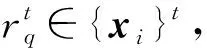
2) 对于每一维, 通过

(9)

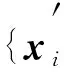
2.3 协同量子粒子群进化算法

基于对量子粒子群优化算法的改进, 本文提出一种精英保留量子粒子群优化算法(D-QPSO). 设在N维搜索空间内有k个粒子, 粒子i由向量(xi,vi)确定, 其中:xi=(xi1,xi2,…,xin)表示粒子i当前的位置;vi=(vi1,vi2,…,vin)表示粒子i的速度. 此外, 粒子也会存储其历史搜索的最优位置pi={pi1,pi2,…,pin}及全局搜索的最优位置pg. 在算法运行过程中, 在每一维度上使用Sigmoid函数将粒子的位置二值化：

(10)

利用粒子迭代过程中产生的启发式信息衡量粒子的可用性. 若两个粒子位置间形成了互斥的运行态势, 则表明两个粒子在不同的峰值上进行寻优, 此时需要将两个位置都记录下来, 从而保证种群的多样性. 引入辅助种群, 将需保留的父代粒子存入辅助种群中. 当整个种群的多样性降低时, 则使用副种群内的粒子信息对粒子位置增加扰动.

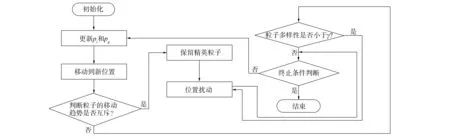
图3 D-QPSO动态多样精英算法流程Fig.3 Flow chart of D-QPSO dynamic and varied elite algorithm

D-QPSO算法的基本流程如图3所示. D-QPSO算法步骤如下:

1) 随机初始化k个粒子{xi(0)=(xi1,xi2,…,xin),i=1,2,…,k}; 设置初始辅助种群A=Ø;

2) 更新个体最优位置pi={pi1,pi2,…,pin}和全局最优位置pg;

3) 通过式(3)～(5)产生新的粒子xi(t+1), 并保留上一代粒子位置;

4) 如果前一代粒子的位置和新的粒子有互斥趋势, 则将上一代粒子移入辅助种群,A={A,xi(t+1)}, 否则转5);

5) 计算新粒子种群{xi(t+1)}的多样性, 如果多样性小于阈值参数γ, 则按式(9)对前t个位置进行扰动;

6) 如果种群满足结束条件则停止, 否则转2).

3 实验结果与分析

下面使用OR-library标准测试数据集测试D-QPSO算法在求解MMKP问题上的性能. 实验比较7种不同算法的结果准确度、 收敛速度及运行时间. 实验使用MATLAB平台, 在处理器为Intel Core 2, 2.66 GHz, 内存为2 GB, 操作系统Windows 7的PC机上运行.

OR-library上的13个标准多维多选择背包测试函数列于表1. 这13个测试用例按个体的分类从5种类别到400种类别不等. 表1中N和n分别表示物品的数量和类数,r表示每类物品内的物品数,m表示资源数量.

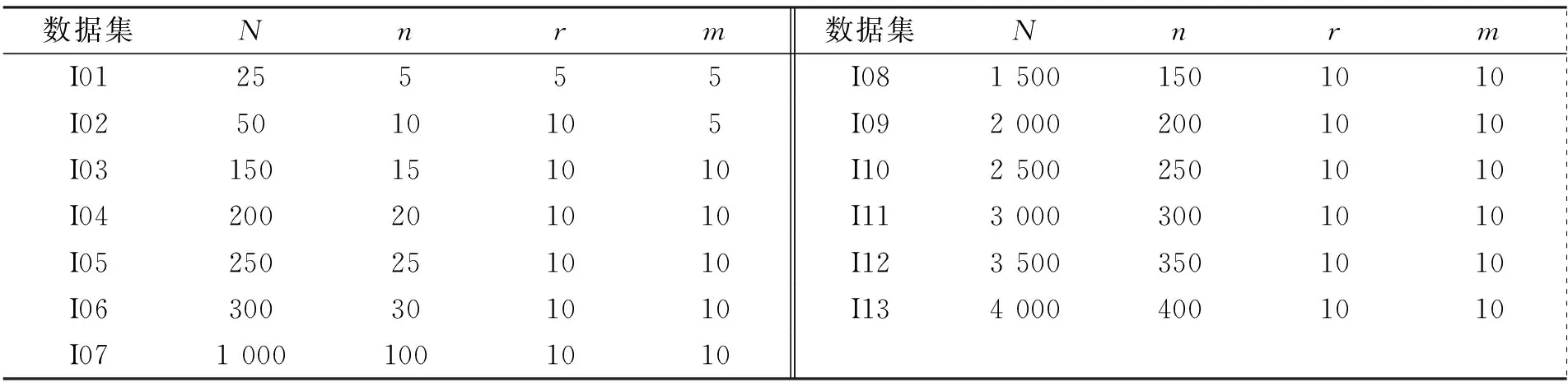
表1 数据集参数Table 1 Parameters of data sets

3.1 最优值比较

实验比较传统粒子群优化算法、 量子粒子群优化算法及两个带有基因变异策略算法的性能. 表2比较了7种不同算法的表现, 包括heu,Cpc,Aut-R,PSO,QPSO,D-PSO和D-QPSO算法. 在参数选择方面, Ant-R算法的参数选择与设置一致; PSO算法是在粒子的运行过程中, 对一定概率的粒子进行Gauss扰动, 惯性权重在运行过程中从0.9到0.4递减, 学习因子C1=C2=0.8,R1和R2是遵循0～1均匀分布的随机数; QPSO算法的吸引收缩因子在[0.5,1]内线性递减; D-QPSO算法中的精英饱和代数定义为t=5, 加速系数rand1和rand2为两个在[0,1]内变化的随机数.

表2 不同算法在13个数据集上的求解准确性比较Table 2 Accuracy comparison of different algorithms on 13 data sets

*表示精确解尚未明确.

由表2可见, D-QPSO算法的求解更接近于全局最优解, 特别当多选择背包内的物品维度较高时优势更明显. 在前7个测试实例中, 由于背包维度不高(n≤100), 所有算法都能获得较好结果. 但当多选择背包内的物品数量增多时, D-QPSO算法获得的值更优. 表明在数据维度增加时, 维度之间的限制更严格, D-QPSO算法跳出局部搜索能力更强, 更易收敛到全局最优解. 虽然在I03,I06和I07上, D-QPSO算法的求解仅次于Ant-R算法, 但两种算法解的差异性较小(0.12%,2.1%,0.03%). 产生这种结果的原因是由于D-QPSO算法在初始化时随机初始化粒子, 而最终结果受初始化影响.

为了更直观地表示, 将所有结果与已有最优值用

(11)

进行归一化比较, 结果如图4所示. 由图4可见, Ant-R,D-PSO和D-QPSO算法的误差率基本小于2%. 加入了精英基因保留策略(D-PSO/D-QPSO)的算法求解值明显好于普通的粒子群优化算法和量子粒子群优化算法, 说明在进化过程中, 采取对有价值信息的保留方法进行变异可增强算法的寻优能力. 当类别数较多时(n>100), D-PSO算法的求解值好于Ant-R算法.

3.2 收敛速度

在背包数量为4 000, 物品种类为400, 每类个体为10个的情形下， 将D-QPSO算法与其他3种算法的收敛情况进行比较, 分别将每种算法运行100次， 计算每种算法每代获得的最优值平均值， 结果如图5所示. 由图5可见, PSO和QPSO算法在处理背包问题时收敛速度较快, 但较易收敛到局部最优解. Ant-R和D-QPSO算法收敛速度较慢, 但能搜索到更优值. 这是因为在D-QPSO算法中增加了对种群多样性的判断, 当种群多样性降低时, 算法加入扰动, 增加了调出局部最优值的可能性, 进而收敛到更优结果.

图4 不同算法的结果误差率比较Fig.4 Comparison of error rates of different algorithms

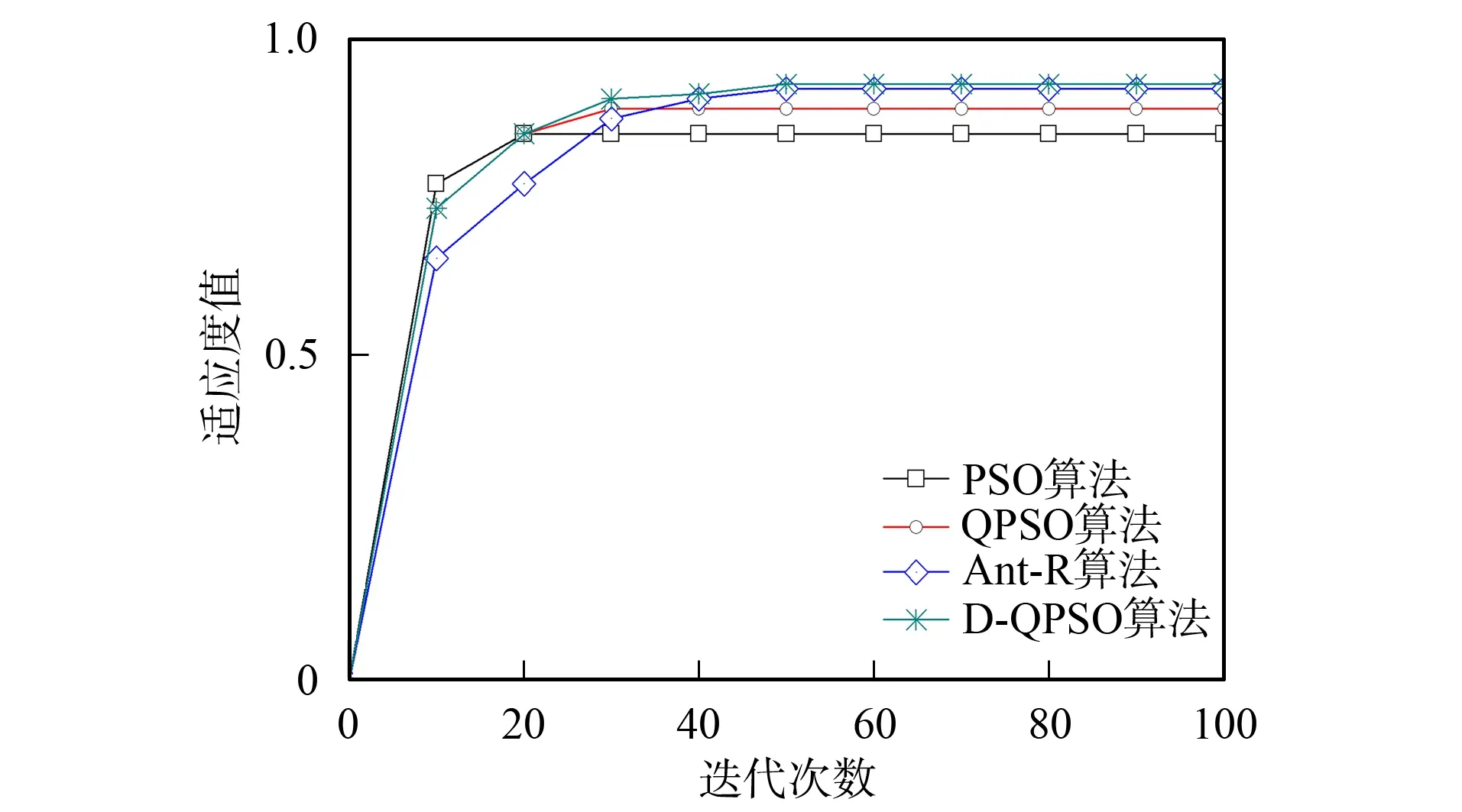
图5 PSO,QPSO,Ant-R和D-QPSO算法的收敛曲线Fig.5 Convergence curves of PSO,QPSO,Ant-R and D-QPSO algorithms

3.3 运行时间

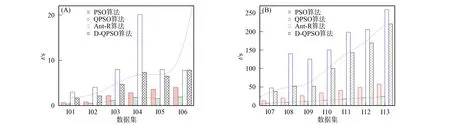
图6 不同算法在13个数据集上的平均运行时间Fig.6 Average running time of different algorithms on 13 data sets

图6是将D-QPSO算法与Ant-R,PSO,QPSO算法分别在13个数据集上运行50次所得的平均运行时间比较结果. 由图6可见, D-QPSO算法的求解时间高于传统的PSO和QPSO算法, 但多数情形下低于Ant-R算法(31.5%). 表明使用量子粒子群优化算法保证了算法的收敛速度. 图6中两条虚线对比了加入精英保留策略与未加入精英保留策略的量子粒子群优化算法求解时间. 结果表明, 虽然增加了精英基因保留策略的算法所消耗的时间高于原始的量子粒子群优化算法, 但随着问题维数的增加, 其增加的时间是多项式倍数的, 可以接受.

综上所述, 本文针对多维多选择背包问题面临的强约束限制、 复杂性高、 易收敛到局部最优解的问题, 提出了一种改进的量子粒子群优化算法. 该算法在进行迭代过程中增加了对基因有效性的判断, 保留了对种群进化意义较大的染色体. 当种群的多样性降低时, 根据已保留的精英基因对现有种群内的个体进行变异, 使算法更易跳出局部最优解. 对本文算法在标准测试数据集上进行了测试, 证明了算法的有效性. 虽然增加了基因有效性判断使算法的时间复杂度增加, 但仍在可接受的范围内.