Theoretic Diffraction Research on the Order-Disorder Effect ofTransition Metal in Li(Ni1/3Co1/3Mn1/3)O2
2018-11-28ChunhuiCaoJianZhangChuanzhengYangandBaojiaXia
Chunhui Cao, Jian Zhang, Chuanzheng Yang and Baojia Xia
(1.Shanghai Institute of Microsystem of Information Technology, Shanghai 200050, China;2.University of Chinese Academy of Sciences, Beijing 100049, China)
Abstract: After describing research status of super-structure for Li(Ni1/3Co1/3Mn1/3)O2, diffraction patterns of Li(Ni1/3Co1/3Mn1/3)O2 in different order parameters have been researched by Powder-cell program, including crystal structure, X-ray and neutron diffraction pattern, anomalous diffraction pattern and comparison of Ni Co Mn in different positions. The influence of order parameters on intensity of matrix and super-lattice diffraction lines has also been analyzed and the summarization and prospect have been made lastly.
Keywords: Li(Ni1/3Co1/3Mn1/3)O2; order-disorder; diffraction
1 Introduction
Due to its high cost and toxicity, commercial cathode material LiCoO2in lithium ion batteries is gradually replaced by Li(Ni, Co, Mn)O2, among which Li(Ni1/3Co1/3Mn1/3)O2is the most competitive for its over-all properties[1-4]. All of these cathode materials have a rhomboidal structure with trigonal symmetry (space group: R-3m, No.166), which is layer-structural with α-NaFeO2. Usually, transition metal ions Me (Ni, Co, Mn) are located in octahedral 3b(0 0 1/2) sites and oxygen anions are in a cubic close-packing, occupying the 6c(0 0z) sites. Lithium cations reside at Wyckoff 3a(0 0 0) sites, represented as [Li]3a[Me]3b[O2]6c. In addition, there are three symmetry operations in this structure, including (0,0,0), (1/3,2/3,2/3), (2/3,1/3,1/3).

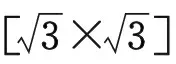
(a) Superlattice of Piled-up
Fig.1StructuralmodelofLi(Ni1/3Co1/3Mn1/3)O2(ReprintedwithpermissionfromKoyamaetal.[11]Copyright2003,Elsevier)

(a) [22.1] (b) [00.1] (c) [11.0]
Fig.2ElectrondiffractionpatternsofLi(Ni1/3Co1/3Mn1/3)O2(ReprintedwithpermissionfromYabuuchietal.[12]Copyright2005,theElectrochemicalSociety)

The super lattice diffraction lines may appear after ordering treatment the order degree has an effect on the diffraction intensity of super lattice line; sometimes the super lattice diffraction lines do not appear but the diffraction intensity of matrix diffraction lines change[19-22]. So we can calculate the order degree by diffraction intensity data, which depends on the crystal structure[23]. In this paper Powder-cell was used to simulate diffraction patterns and intensity of the super and matrix lattices.
2 Crystal Structure


Table 2 The atom positions in different order degree
3 X-ray and Neutron Diffraction Pattern
Figs.5 and 6 show the diffraction patterns of X-ray and neutron at differentS, and the specific data is listed in Table 3. As we can infer from the comparison data, there are obvious difference between the XRD pattern and neutron diffraction pattern. Three strength lines are distinct, the first strength line is different. The second strength lines decrease with the increase ofS, but the third lines are almost constant. This is because that the scattering factors of Ni, Co, Mn have little difference for X-ray, while the difference for neutron is much larger. So the problem of order occupying position of neighboring atom is often studied by neutron diffraction[7].

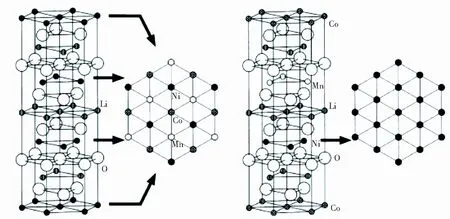
Fig.4 The crystal structure model of Li(Ni1/3Co1/3Mn1/3)O2 when S was 0 and 1
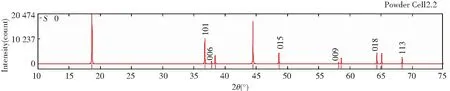
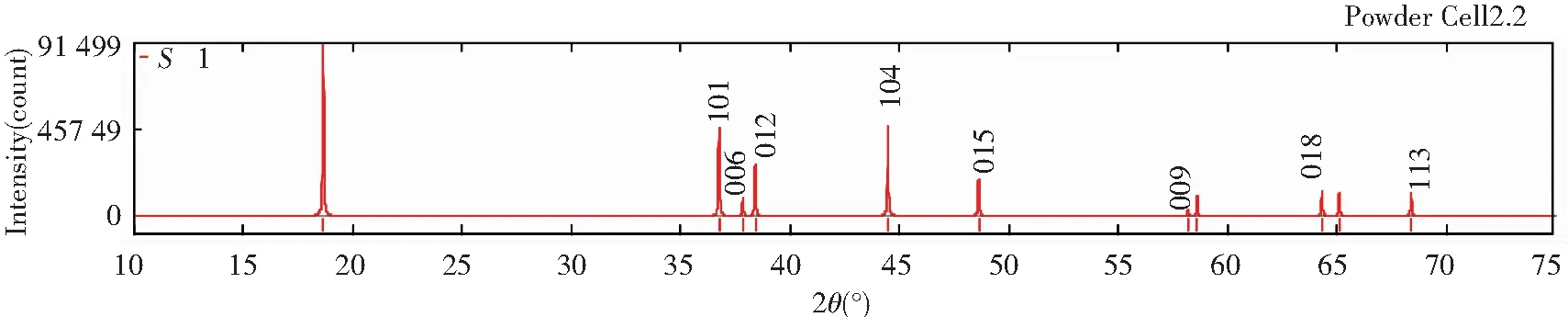
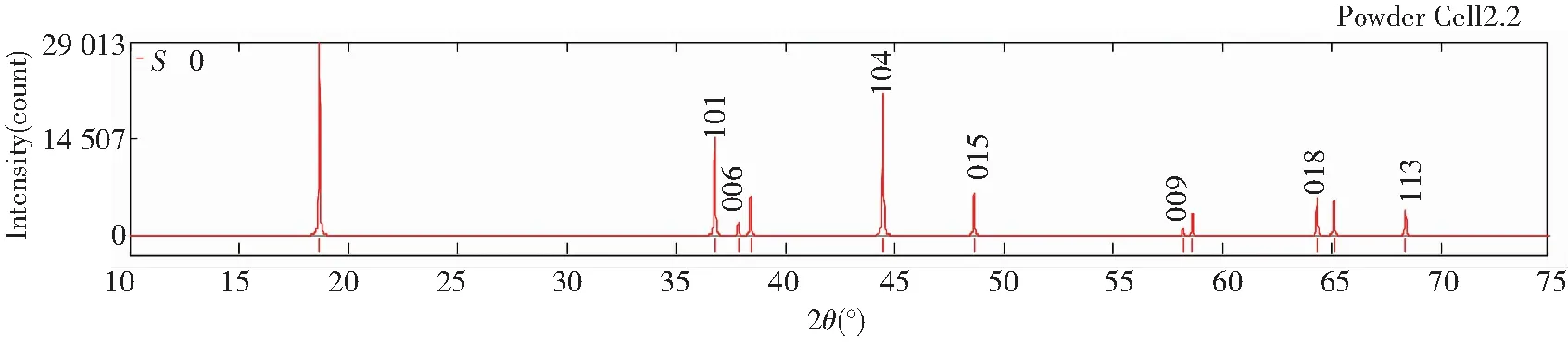
Fig.5 XRD patterns of Li(Ni1/3Co1/3Mn1/3)O2 at S=0, 0.5 and 1 (λ=1.540 6 Å)



Fig.6 Neutron diffraction patterns of Li(Ni1/3Co1/3Mn1/3)O2 at S=0, 0.5 and 1 (λ=1.540 6 Å)

Table 3 Relative diffraction intensity of X-ray and neutron at different S (λ=1.540 6 Å)
4 Comparison of Ni, Co, Mn Occupied in Different Positions
The diffraction data was listed in Table 4 whenS=1 and Ni, Co and Mn occupied in different position. It is known from the comparison that three strength distribution and relative intensities are the same and their structure amplitudes are similar.

Table 4 Diffraction data when Ni, Co and Mn occupy in different positions (λ=1.540 6 Å)
5 Anomalous X-ray Diffraction Pattern
The anomalous diffraction is a diffraction experiment one using the radiation of some element’s absorbing wavelength as incident ray, called as the anomalous scattering or anomalous diffraction, which is also called diffraction of choosing elements.
When there is anomalous diffraction, the total atomic scattering factor is given by:
(1)
wheref′ andf″ are the real and imaginary parts of anomalous diffraction correction,f′ andf0have the opposite phases, the phase off″ is 90°. Andfis:
(2a)
The approximate form is:
(2b)
The effects of anomalous diffraction on total scattering factor are as follows:
1) Anomalous diffraction can be ignored when the incident ray’s wavelength is far from absorbing limit;
2) Near the absorption limit, anomalous scattering correction is quite large and increases with the scattering angle;
3) When the incident ray’s wavelength is equal to absorption limit, anomalous diffraction can play a dominant position at high diffraction angles;
4) Anomalous diffraction correction is related to the atom number of the scattered due to different element has different absorbing limit.
So we can study the long range order of neighboring atoms by anomalous diffraction in principle. As seen from Table 5, the position of diffraction lines increases with the wavelength and moves to the high angle, while the relative intensity has no change. It seems that anomalous diffraction has no effect, but actually possible cause is that Powdercell could not carry out the correction of the anomalous scattering.

Table 5 Comparison of anomalous diffraction data at S=1
6 Influence of Order Degree on Intensity of Matrix Diffraction
The analysis shows that the order of Ni, Co and Mn in the 3bposition has little effect on the matrix diffraction relative intensity for both the conventional and anomalous X-ray diffraction.
Under symmetric Bragg reflection geometry condition in the X-ray powder diffraction, the relative integral intensity for single-phase can be expressed as follows:
(3)
wherePhklis the multiplicity factor of crystal plane (hkl),Fhklis structure factor, the last is angle factor. The formula of structure factor is:

lzj)+isin2π(hxj+kyj+lzj)]
(4)
wherefjis the scattering factor ofjatom.xj,yj,zjis the coordinate ofjatom. Summation is for all atoms in single cell. Specifically for Li(Ni1/3Co1/3Mn1/3)O2, they contain 3 Li atoms, 3 transition metal atoms and 6 oxygen atoms. The position parameters of main diffraction lines are listed in Table 6.
Supposef3a,f3b,f6care the atom scattering factor of atoms on 3a, 3band 6cposition, then we get the following formula for Li(Ni1/3Co1/3Mn1/3)O2:
(5)
f3bis complicated, whenS=0,
(6)
whenS=1
f3b=fNi+fCo+fMn
(7)
when 0 f3b=S×(fNi+fCo+fMn)+ (8) Eq.(8) shows that, when 0 Similarly,the diffraction angle factor(1+cos22θhkl)/ (sin2θhklcosθhkl) decreases with 2θincreasing. The specific values can be calculated or obtained from professional books. Thus,main characters of each diffraction lines of Li(Ni1/3Co1/3Mn1/3)O2can be summarized as follows: (1)Considering the contribution of oxygen on 6cposition to diffraction intensity, it can be divided into: No contribution: 003,101,015,009,107,018,113; The addition: 104, 110; The subtraction: 006, 012. Table 6 Atom position parameters of (2)Considering the contribution of atoms on 3aand 3b, it can be divided into: The addition: 006, 012, 104, 110, 018; The subtraction: 003, 101, 015, 009, 107, 113. (3)The“addition” and “subtraction” relationship reveals a very important rule. Take 003, 101 and 104 as examples,Fhklis : (9) The diffraction line 104 is stronger than 101. The first part in the formula is the contribution of Li atoms; the second part is the contribution of orderly Ni, Co,Mn on 3b; the third part is the contribution of randomly Ni, Co, Mn on 3b; the fourth part is the contribution of oxygen on 6c. It can be inferred from Eq.(9) that the contribution of 3aand 3bto 003 and 101 is subtraction, for both 003 and 101 oxygen have not contribution. While contribution of 3aand 3bto 104 is addition. WithS=0, 0.2, 0.4, 0.6, 0.8, 1.0, the relative intensity of the calculation results (as shown in Table 8) and analysis results show that there is no influence of order degree on diffraction intensity matrix lines. In other words, the diffraction intensity of matrix lines has no relationship with order and disorder in the 3bsite. Therefore the order degree,S, cannot be solved from the diffraction data of matrix lines. It is known from the above research that the ordering on 3bpositions does not show diffraction lines of super-lattice for Li(Ni1/3Co1/3Mn1/3)O2belong to the No.166 space group structure. In order to prove whether it is right, the author has made a simulated study diffraction patterns of the classic AuCu3super structure. The result shows that only when the use of crystallographic position are the same, but space group (extinction rule) is different, (No.225, Fm-3m and No.221, Pm-3m), diffraction pattern calculated can show the super-lattice lines. It can derive from his conclusion that above simulated diffraction patterns using No.166 space group do not appear super-lattice lines cannot prove that the diffraction pattern of Li(Ni1/3Co1/3Mn1/3)O2with super-structure cannot appear super lattice lines. In the rhombohedral system with space group (No.143-No.167) was not found corresponding space group whichx,y,zcoordinates are the same with (3b) positions in No.166 space group and the extinction conditions are different. That No.166 after (3b) ordering has symmetry of P3112 (No.151)18is questionable, becausex,y,zcoordinates of atoms are obviously different and extinction rule is similar between No.151 and No.166 space group. To this end, wecalculated the crystallographic position parameters of space group No.166 may appear the super-lattice lines: 001, 002, 004, 111, as shown in Table 7. Table 7 Position parameters of space group No.166 We can conclude from analysis of Table 7: (1)The 3aand 6cposition atoms are no contribution to the diffraction intensity of 001, 002, 004 and 111. (2) 3bposition atoms contribution to the diffraction intensity are more complex; when disordered (S=0) occupation, the atomic scattering factors for each position are equal to (fNi+fCo+fMn)/3 the same, such as, factor scatter factor for each position, the contribution of three position is equal to zero; when totally ordered (S=1) occupation, the scattering factors of three position are different, the contribution of three positions is not zero, then the super-lattice lines can appear; and the larger the difference of atomic scattering factor between the three positions is, the stronger super-lattice line is. Therefore, using the anomalous diffraction techniques or/and neutron diffraction is beneficial to studying a super-lattice structure. (3)When 0 The effect of order degree on the diffraction intensity has calculated using the data given in Table 8, because 104 and 111 almost overlap, so only for four diffraction of 002, 003, 004, 101 was calculated. The results are given in Table 9. We can see from analysis of Table 9: (1) The matrix diffraction intensity does not change withS, in other words, the diffraction intensity of matrix line is not influenced byS; (2) Diffraction intensity of super-lattice lines increases with the increase ofS, which can solve an order degree,S, according to the intensity data super-lattice diffraction lines or super-lattice and matrix diffraction lines. (3) The relative intensity of super-lattice lines is very weak, evenS=1, the relative intensity of 002 and 004 super two points front is only 0.225% and 0.043%. So the general diffraction experiment is very difficult to detect the super-lattice lines. Table 8 The relative parameters of several matrix and super-lattice lines Table9Calculatedintensityandrelativeintensityofseveralmatrixandsuper-latticelinesandinfluenceoforderdegree SIntensity002003004101Relative intensity0020030041010.00635 262.9630321 050.8750100.00050.540.218.164 0635 262.96310.910 0321 050.8750.002 9100.000.001 750.540.4228.926 0635 262.96343.476 0321 050.8750.036 0100.000.006 850.540.6515.106 3635 262.96397.831 4321 050.8750.081 1100.000.015 450.540.81 216.302 1635 262.963173.793 2321 050.8750.191 5100.000.027 450.541.01 431.104 0635 262.963271.747 0321 050.8750.225 3100.000.042 850.54 For Li (Ni1/3Co1/3Mn1/3)O2, when Ni, Co, Mn ordered occupied in 3b, diffraction intensity of the matrix lines is not influenced by order degreeS; but the diffraction intensity of super-lattice lines increase with the order degree. Theoretically, one can solve an ordering degree,S, according to the intensity data super-lattice diffraction lines or super-lattice and matrix diffraction lines, but it is very difficult because diffraction intensity of the super-lattice lines is very weak, in general diffraction experiments. Therefore,whether orderly occupying is existed in 3bof Li(Ni1/3Co1/3Mn1/3)O2and forms of super structure still need further study in the following aspects: 1) To explore the optimal process of ordering treatment for Li(Ni1/3Co1/3Mn1/3)O2material under the appropriate medium temperature; 2)To enhance the detection ability of diffraction experiment, use strong X-ray source, such as synchrotron radiation X-ray source, use high efficient detector, super fine experimental operation, such as slow speed scan and anomalous diffraction techniques or/and the neutron diffraction technique; 3) According to the relationship between diffraction intensity increases with the order degree increases, to determine the order degree of material; establish the relationship among ordering treatment process, order degree and materials (battery) performance.
7 Influence of Order Degree on Intensity of Super-lattice Diffraction Line


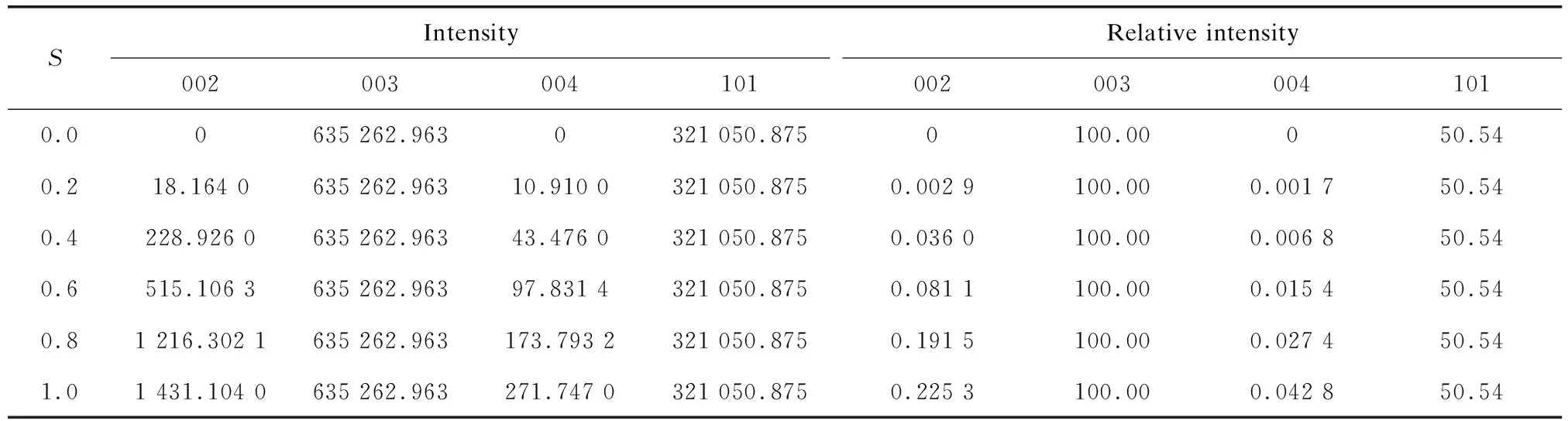
8 Conclusion and Prospect
杂志排行
Journal of Harbin Institute of Technology(New Series)的其它文章
- Review:A Survey of Single Gimbal Control Moment Gyroscope forAgile Spacecraft Attitude Control
- Inverse Synthetic Aperture Radar Imaging of Multi-TargetsBased on Image Processing Technique
- Dynamics Analysis of Square Unit and its Combined Mechanismwith Joint Clearance
- Experimental Study on Shear Behavior of New-TypeSteel-Concrete Composite Bridge Deck
- Review:A Critical Assessment on the Predictability of 14Micromechanics Models for the Stiffness and Strength ofUD Composites
- Three-Dimensional Normal Stress for Controlling Electronic Structureand Magnetic Property of Fe2Ge
