基于偏最小二乘回归的高速公路运营期碳排放计量模型∗

岳鹏程

（山西省交通科学研究院 太原 030006）

1 引言

高速公路运营阶段，车辆行驶所产生的碳排放量被称为高速公路运营期碳排放量［1］。近年来，随着私家车保有量的激增以及快递行业的快速发展，高速公路运输量成几何增长，造成高速公路运营期通行碳排放成为我国温室气体污染的重要来源［2～3］。研究高速公路运营期通行碳排放的计量技术具有重要的现实意义，能够为高速公路实现低碳运营提供科学的数据支撑，为管理部门科学制定合理的减排目标以及评价减排措施实施效果提供决策依据［4］。

我国碳排放检测技术的发展尚处于初级阶段，存在颇多缺陷，传统的化学检测为接触性检测技术，时效性差，不能用于实时监测。新兴的光学检测技术可支持非接触性检测、响应时间短，但是测量精度受环境因素影响显著，且造价高昂［5］。而高速公路运营期通行碳排放测量环境为户外，长期受气象条件（温度、湿度、压力等）影响，且碳排放源为高速移动的车辆，显然，依靠硬件设备的碳排放检测技术不能满足计量要求［6］。与设备计量技术相比，软测量技术计算灵活，时效性好，节约成本，无需专人维护，符合可持续发展理念，可满足高速公路碳排放的计量要求。

目前，对交通碳排放软测量的研究大致分为两种方式［7～10］：一种是“自上而下”的方式，即考虑工业化水平、人口、能源消耗强度、人均GDP等宏观因素与碳排放之间的关联关系，构建碳排放计量模型，常被用于区域交通碳排放的研究中，国际上常用的模型包括 STIRPAT 模型［11］、COPERT 模型、CMEM模型等，不适用于高速公路碳排放计量。二是“自下而上”的方式，即研究车流量、里程、车型、自然因素等微观影响因素与碳排放之间的定量关系，该计量方式能够具体到某条高速公路、某个路段、某个时间段，符合高速公路运营期通行碳排放计量的实际要求［12～15］。长安大学的刘荔等应用“自下而上”的方式在高速公路运营期通行碳排放方面做了些研究，她假设变量间相互独立，对车辆运行速度与碳排放、道路坡度与碳排放、路面平整度与碳排放的定量关系分别进行了单独拟合，建立了碳排放的计量模型［16］。但是，研究表明高速公路运营期通行碳排放的影响因素之间并不完全相互独立，还存在相关关系，如果不考虑因素间的相关关系而直接通过非线性拟合建立模型，模型的精度和稳健性都会受到影响［17］。本文旨在改进当前碳排放模型的建模方法，消除因素间的多重相关性对建模造成的影响，提高模型的精度。

2 PLS在高速公路运营期碳排放中的应用

在高速公路通行碳排放的回归建模与分析工作中，研究人员往往为了更完备地描述系统，不遗漏每一个系统特征，会尽可能多地选取包括气象条件、道路因素、车辆因素、驾驶员行为等可能影响交通碳排放的因素。事实上，这些影响因素间存在同步波动的趋势，彼此间有影响，这样的多变量系统中必然会存在变量多重相关的问题。变量间的多重共线性严重损害建模时回归系数的估计，进而降低模型的稳健性，损害模型精度［18］。

本文将偏最小二乘回归方法应用于高速公路运营期通行碳排放的回归分析中，改进了传统的“自下而上”的交通碳排放软测量技术。偏最小二乘回归（Partial Least-squares Regression，PLS）是1983年由伍德和阿巴诺等提出的一种新型多元统计数据分析方法，在解决自变量多重相关性危害回归模型的问题上具有独特优势。该方法有别于传统回归方法，在回归建模中，不直接考虑因变量与自变量总体的回归建模，而是采用成分提取技术和综合筛选的方式处理回归系统中的数据信息，获得若干对因变量具有最佳解释能力、最大影响力的新的综合变量，所建模型辨识了系统中的信息和噪声，能有效克服回归建模中自变量间存在多重相关性对模型造成的不良影响［19～20］。

3 数据处理和模型构建

本文旨在探讨消除因素间相关关系对高速公路运营期通行碳排放计量模型精度的影响，因此在所有高速公路运营期通行碳排放影响因素中选取相关关系显著的车辆运行速度和道路坡度两个碳排放因素作为主要研究对象，通过对比试验验证消除此两因素间的相关关系能有效提高模型精度。

基于长深高速公路山东段小汽车的试验数据，应用偏最小二乘回归确定模型的系数，建立基于偏最小二乘回归的高速公路运营期碳排放计量模型。

3.1 标准化和多重相关性校验

对车辆运行速度x（1km/h）、道路坡度x（2%）和每百公里碳排放量y（kg/100km）的样本矩阵按式（2）和式（3）进行标准化处理，消除不同变量间数量级和量纲上的差别。记因变量y的标准化矩阵为B0=(̂)n×1，自 变 量x1和 x2的 标 准 化 矩 阵 为A0=()n×2，n表示样本数据容量。

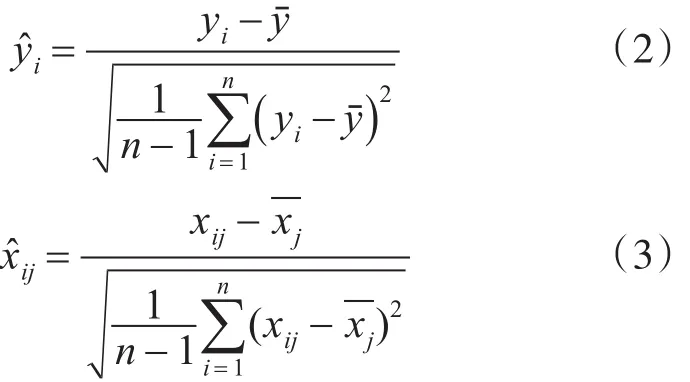
表1 相关系数矩阵

从表1列出的相关关系矩阵可以看出车辆运行速度x1与道路坡度x2的相关系数rx1x2=-63.22%的绝对值小于小汽车每百公里的碳排放量y与道路坡度x2的相关系数rx2y=88.03%，但是大于小汽车每百公里的碳排放量y与车辆运行速度x1的相关系数rx1y=-42.34%的绝对值，即自变量间的相关关系大于因变量与自变量的相关关系，可见车辆运行速度与道路坡度并不独立，变量间存在共线性，且会对碳排放模型产生严重影响，需要重新提取对因变量解释能力更强的特征值。

3.2 影响碳排放的新综合变量的提取

通行碳排放模型研究的是碳排放与各影响因素之间的数学关系，只有一个因变量碳排放，属于单因变量的偏最小二乘回归范畴，成分提取时只处理自变量数据阵X。自变量数据阵包括车速的平方、车速和道路坡度三个因素，即X的秩r≤3最多提取三个成分u1、u2和u3，提取的步骤具体如下：

1）第一成分的提取

从自变量数据阵X中提取第一个成分u1，u1表示为自变量集的线性组合，如式（5）。

带入自变量标准化矩阵，得第一成分u1的得分向量为 û1，如式（6）。

根据主成分分析原理与典型相关分析的思路，u1应尽可能多地提取自变量阵的变异信息，且与y的相关程度最大，数学表达式为

利用Lagrange乘数法推导第一主轴w1的计算公式为式（8）：

2）建立X和Y对u1的回归模型

假定回归模型为

式中 p1和r1分别表示回归模型中的参数向量，最小二乘估计为，A1和B1分别表示回归方程的残差矩阵，表达式为式（10）：

3）用残差矩阵 A1、B1代替 A0、B0重复以上步骤

检查模型拟合精度，残差阵A1中元素的绝对值大于0，继续令 A0=A1，B0=B1，对残差矩阵进行新一轮的成分提取和回归分析，得到成分u2。即

X和Y对u1和u2的回归模型：

同理可得到u3。

4）成分解释能力和交叉有效性检验

通常，偏最小二乘回归分析方法在建立回归方程式时并不需要将所有成分都选用进来，而是有针对性地选用其中的一部分就可以得到预测能力较好的回归模型［21］。通过解释能力、累积解释能力和交叉有效性检验来确定建模所需提取的成分。成分提取校验表如表2。

表2 成分提取校验表

从上表可以看出在进行交叉有效性校验时，主成分u1对碳排放的解释能力R2高达84.63%，前两个成分u1和u2的累积能力R2累积达到92.77%，而u3对碳排放的解释能力只有1.93%，虽然u3成分的交叉有效性值也大于0.0975，但是它对因变量y的解释能力有限，因此偏最小二乘回归时只提取前两个成分，最终得到偏最小二乘回归模型为

绘制的三维曲面图如图1所示。

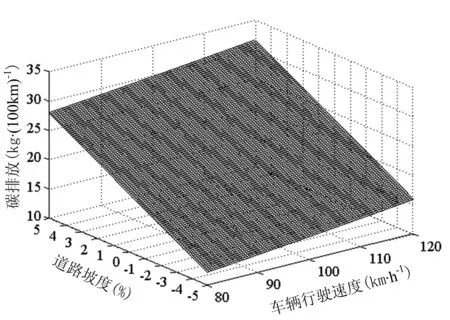
图1 模型三维曲面图

4 结语

样本数据的偏最小二乘拟合回归结果与最小二乘拟合回归结果对比如表3，两种方法的拟合值和实际值拟合曲线分别如图2和图3所示。可以看出偏最小二乘拟合回归的拟合值和实际值的最大相对误差仅为8.7%，拟合值和实际值拟合曲线的斜率为0.9296，模型拟合效果好，相关系数的平方为0.94121，而最小二乘拟合的拟合值和实际值的斜率为0.6402，相关系数的平方为0.8080，最大相对误差为25.95%，约为偏最小二乘回归的最大相对误差的3倍。

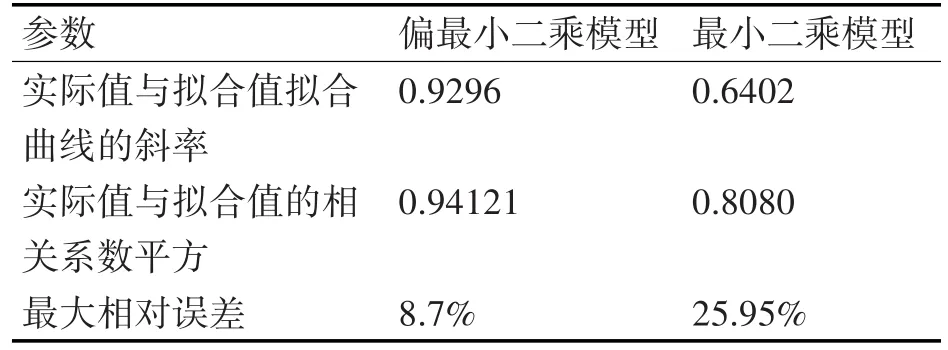
表3 两种模型的比较结果

综上所述，在计算高速公路车辆碳排放时，如果不考虑影响因素间的相关关系，直接建立拟合模型，模型的精度和稳定性得不到保证，也说明本文将偏最小二乘方法应用于高速公路车辆碳排放的预测模型中，能够消除变量间相关关系给模型造成的不良影响，与最小二乘回归结果的比较，预测值与实际值的最大相对误差仅为8.7%，远小于最小二乘回归模型，模型精度得到有效提高。但是文中只是有针对性地选取存在相关关系的两个影响因素对高速公路碳排放的影响，验证了方法在高速公路车辆碳排放应用的可行性，后续研究还可以将气象条件、道路因素、车辆驾驶员行为等更多的影响因素考虑进来，丰富不同车型数据，建立更加全面的碳排放计算模型。所建模型对城市交通的碳排放量计量同样具有参考价值。

图2 PLS模型实际值和拟合值的关系曲线

图3 LS模型实际值和拟合值的关系曲线