基于功率平衡策略的可再生能源电网储能机制研究∗

陈明彩

（山东科技职业学院建筑工程系 潍坊 261053）

1 引言

与高渗透率电网不同［1］，可再生能源电网是风电、光电（光伏发电、光热发电）等不确定性可再生能源为主力电源的电网［2～4］。由于其不确定性，风电、光电等可再生能源的发电功率不具备平衡随机性负荷的能力［5］。解决不确定性问题的消纳法对低渗透率、高渗透率电网行之有效，但对可再生能源电网却力不从心［6］，可谓“防渗不防漏”，必须依赖储能设施。储能设施，如抽水蓄能电站［7］，由于其响应速度快、可储可发，能有效地平抑风、光等能源产生的功率波动，将“劣质”能源转换为受端可接受的优质清洁能源，实现能量在时间上“腾挪”。在可再生能源电网中，为了应对其随机波动的失衡功率，要求储纳式抽水蓄能电站容量更大、随动性更强、状态切换更频、利用小时更长［8］。

本文聚焦基于大容量储能设施的储纳机制，阐述其核心内涵，描绘其整体廓线，并探讨可再生能源电网规模与储能设施之间合理的容量关系。

2 可再生能源电网

电网发电功率具有不确定性，调度运行须用不确定性的发电功率去平衡随机性的负荷［9］。除非采取措施，否则将出现不平衡功率，即失衡功率，不确定性可再生能源电源（UREP）比重越大。问题越严重。

自然功率是完全由不确定性一次能源决定的UREP发电功率。在任意时刻t，设Pu(t)为UREP自然功率，Pl(t)为负荷功率，前者不确定，后者随机。将UREP与负荷合并为等效负荷，不确定性的等效负荷功率PΔ(t)为Pl(t)-Pu(t)。约定等效负荷功率具有负荷属性，就是PΔ(t)≥0。等效负荷的概念将可再生能源电网功率平衡问题转化为用确定可控的电源平衡不确定的负荷。设Pc(t)为常规电源功率，Pn(t)为网络损失功率，电网的失衡功率ΔP(t)为 PΔ(t)+Pn(t)-Pc(t)。若不计网络损失功率，简化为

显然，ΔP(t)＞0，失衡功率为负荷属性，ΔP(t)＜0 ，失衡功率为电源属性。时段 [t0，t]内，失衡功率ΔP(t)积累成的失衡能量E(t)为

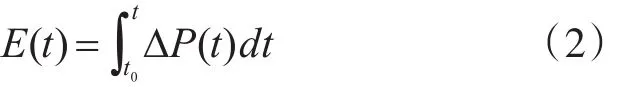
定义失衡度δ(t)为失衡功率ΔP(t)与自然功率Pu(t)的比值，是UREP功率损失的相对值，即

均方根失衡度T描述时间周期[0，T]内电网整体的功率失衡情况，定义为

取T=8760h，由式（4）表达年均方根失衡度δY。三种电网，年均方根失衡度δY的范围分别为

1）δY＜10%，低渗透率电网；

2）10%≤δY＜30%，高渗透率电网；

3）δY≥30%，可再生能源网。

可再生能源电网有多种规模形式，诸如可再生能源微网、配网、市网、省网和大区网，可再生能源电网已经在丹麦诞生，在中国即将诞生［10］。研究可再生能源电网的规划设计、调度运行，意义重大。

3 储能设施运行

储能设施在容量约束下运行，包括装机容量PM、能量容量EM。设PsM、PgM分别为储能装机容量、发电装机容量，两者相等可统一为PM。设Pst(t)为储能设施功率，Pst(t)＜0是储能功率，Pst(t)＞0是发电功率，设Est(t)为存储能量。这样，功率约束为

能量约束为

图1是储能设施运行状态图。图中，上界是能量库容EM，下界对应零能量状态；左界是储能装机，右界是发电装机。M(t)是运行点，M(t0)是初始点。左边是储能状态，右边是发电状态，纵轴对应储能、发电的状态切换，或对应停机状态。

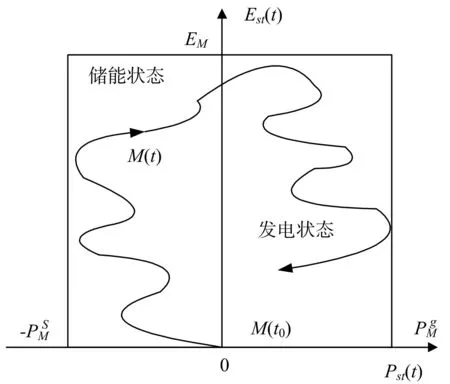
图1 储能设施运行状态图

储能设施的存储能量Es(t)为

其中，ρst是效率系数，储能状态、发电状态有各自的效率系数 ρst，Es(t0)是初始存储能量。运行轨迹具有单调性，储能状态时存储能量Es(t)单调上升，发电状态时存储能量Es(t)单调下降。运行点具有时变性，M(t)总处于运动之中，除非处在纵轴上。可再生能源电网需要容量大、技术成熟、成本低廉的储能设施，抽水蓄能电站是目前的最佳选择［11］。

4 储纳运行机制

4.1 储纳机制

以图2的四元单母线可再生能源系统为背景阐述储纳机制。

三层调度过程［12］：第一步是日前发电计划，电源功率平衡负荷功率日前预测值；第二步是实时发电计划，调整电源功率，平衡负荷实时预测值与日前预测值的差值；第三步是自动发电控制，AGC装置自动平衡负荷实际值与实时预测值的差值。完整调度周期示意如图3所示。

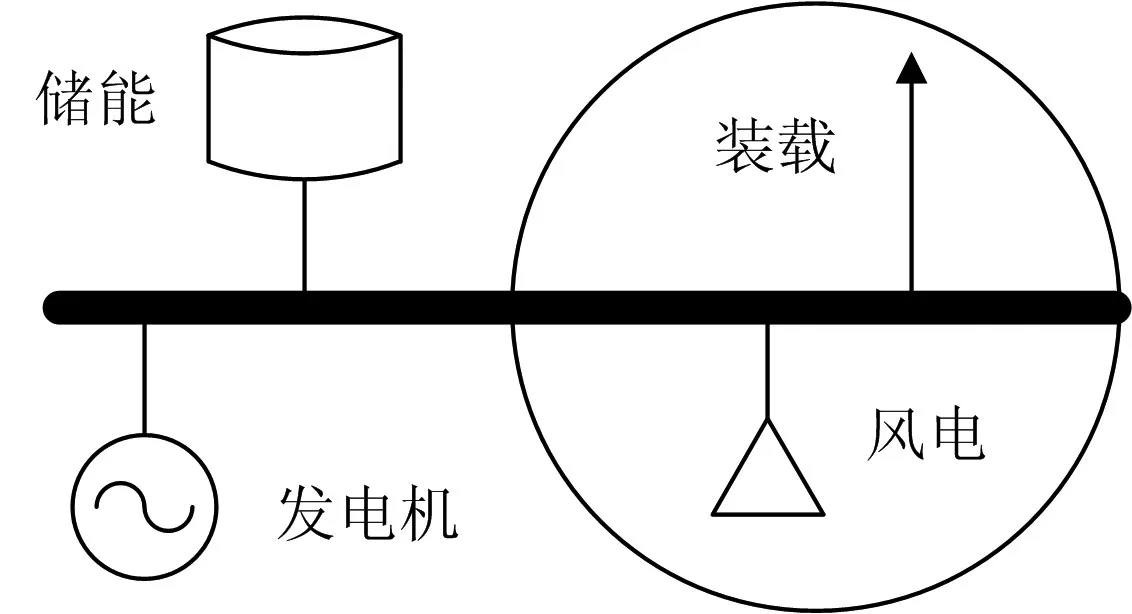
图2 四元单母线可再生能源系统

图3 完整调度周期示意图

日前发电计划：用常规电源功率Pc(t)平衡等效负荷功率PΔ(t)日前预测值(t)，即

实时发电计划，储能设施功率Pst(t)可正、可负，兼具发电、负荷属性，以平衡等效负荷功率PΔ(t)实时预测值(t)与日前预测值(t)的差值，即

自动发电控制，AGC功率Pa(t)平衡等效负荷功率 PΔ(t)实际值 PΔ(t)与实时预测值的差值(t)，即

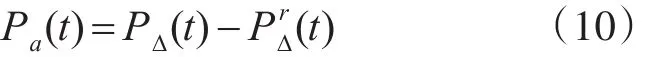
上述三式相加，得到功率平衡方程

即

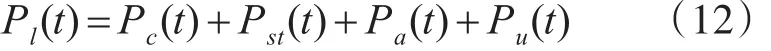
上式表明，日前调度、实时调度及自动发电装置前赴后继，在UREP发电功率极大化的前提下实现了电网功率平衡目标［13］。以往的电网，用可控的常规电源去平衡随机的负荷，可再生能源电网，用可控的常规电源、可控的储能设施去平衡不确定的等效负荷 Pl(t)，两者既相似又不同［14］。将式（11）变形为

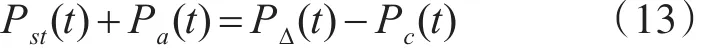
比照式（1），有

此式与式（12）本质相同，却更体现储纳法的核心内涵：失衡功率ΔP(t)由储能设施和自动发电控制装置平衡，或者说，失衡功率ΔP(t)主要由储能设施平衡。

4.2 约束运行

储能设施必须在其装机容量、能量容量限定的范围内运行。超出边界，须调整常规电源弥补储能设施能力的不足。储纳法与消纳法相结合，呈现出储纳为主、消纳为辅，合力平息功率不确定性的局面。

储能设施的四种约束运行状态对应四种储纳［15］、消纳的结合状态，具体如下：

1）运行点处于能量容量时，失去继续储能的能力，此时，须减小常规电源功率，消纳多余的电能；

2）运行点处于零能量时，失去继续发电的能力，此时，须增加常规电源功率，弥补电源的不足；

3）运行点处于储能装机容量时，储能功率不能继续增加，此时，须减小常规电源功率，消纳多余的发电功率；

4）运行点处于发电装机容量时，发电功率不能继续增加，此时，须增加常规电源的功率，弥补发电功率的不足。

4.3 失衡成因

式（9）、式（10）相加，有

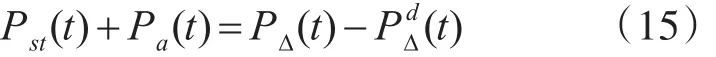
比照式（14），有

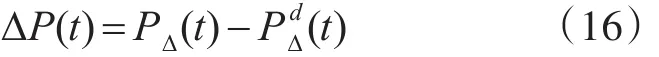
即失衡功率ΔP(t)完全由日前预测误差引起。不确定性表现为难以预测性，式（16）刻画了UREP功率不确定性的本质。

5 储能设施容量

储能设施的容量应满足可再生电网平息功率不确定性的需求。容量不足的储能设施将频繁触界，能量吞吐作用受到限制［16］。UREP的发电功率具有不确定性，规划和设计储能设施容量时应采取概率统计的方法。

5.1 装机容量

储能设施应具备吞吐失衡功率ΔP(t)的能力。将年度均方根失衡度δY等效为

其中，ΔP(t)是按年统计的年失衡功率，Pu(t)是按年统计的年自然功率。储纳设施的功率容量PM应满足平衡年失衡功率ΔP(t)的条件，即

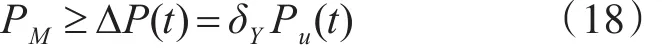
5.2 能量容量

日最大失衡负能量指每日连续负值失衡功率绝对值|ΔP(t)|时间积分的最大值。第i日的日最大失衡正能量为

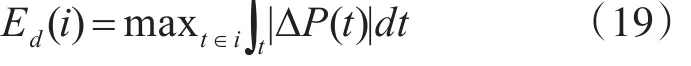
据此，年均方根失衡正能量EY定义为如下的概率统计值：

考虑储能效率系数 ρst，储能设施的能量容量EM应满足关系：

定义储能利用小时T如下：

即储能利用小时T描述了装机容量、能量容量之间的关系。

6 算例分析

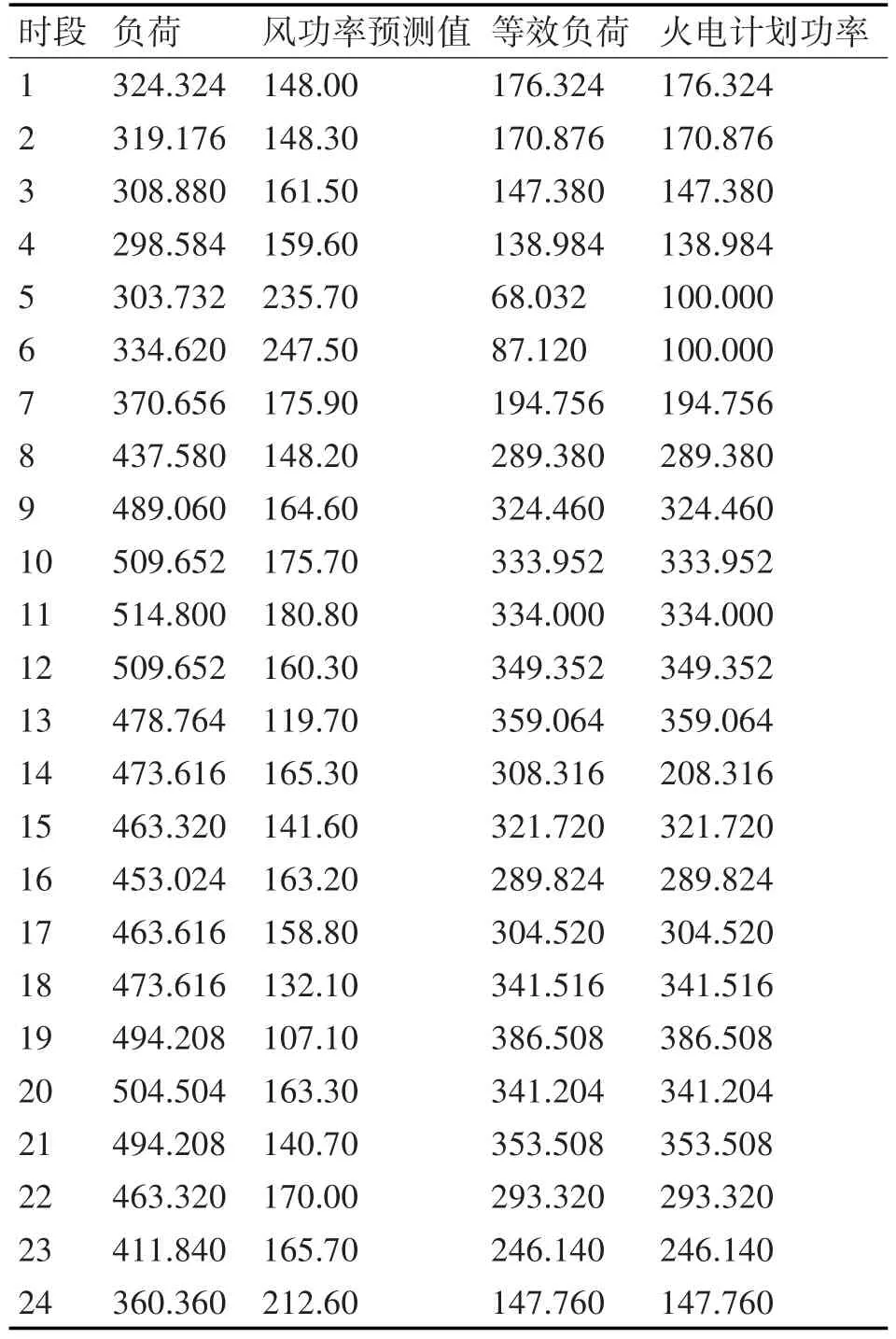
表1 简单系统日前发电计划值（/MW）

站，一个风电场，一个负荷，采用本文所提的储纳机制进行调度运行。选取IEEE-RTS 96负荷及NREL公布的某风电场3月15日数据作为典型日数据进行分析。假设抽水蓄能电站的额定功率PM=100MW，能量库容EM=1000MWh。抽水蓄能电站的初始能量库容设定为0.5(Emax+Emin)。简单系统次日各时段的日前发电计划值如表1所示，简单系统各时段的实时调度值如表2所示。

表2 简单系统实时调度值（/MW）

在实时调度过程中，抽水蓄能电站能量—功率运行状态如图4所示。抽水蓄能电站在3：00～4：00、10：00～12：00运行于功率约束边界，没有达到过能量库容的上限。

图4 抽水蓄能电站能量-功率运行图

7 结语

可再生能源电网是不确定性可再生能源为主力电源的电网。针对可再生能源电网产生的失衡功率，本文提出平衡功率的储纳法，并基于储纳法阐述用于可再生能源电网调度的储纳机制。储纳运行机制由日前调度、实时调度及自动发电装置三个环节衔接而成，分别平衡等效负荷功率的日前预测值、实时预测值与日前预测值的差值、实际值与实时预测值的差值。

储能设施是制约储纳机制实施的关键因素。在装机容量和能量容量的约束下，储能设施以能量腾挪、功率平衡为基本特征平息电网的功率不确定性。储能设施的运行轨迹具有单调性，运行点具有时变性。并且可再生能源电网规模应该与储能设施容量协调适应，储能设施容量应满足可再生能源电网的需求。

利用四元单母线可再生能源简单系统算例，验证了本文所提策略的可行性。结果表明，抽水蓄能电站应对不同的调度过程，能快速切换“储能-发电”状态，可以有效地平抑可再生能源发电的不确定性。