兼顾带宽和开销的网络最优路径算法∗

马慧慧 卢 昱 陈兴凯

（1.军械工程学院信息工程系 石家庄 050003）（2.军械工程学院装备指挥与管理系 石家庄 050003）

1 引言

随着网络技术的发展，人们对于大数据量传输的需求持续增加，迫使研究者不断寻求新的解决办法来满足这种需求。最优路径问题是网络分析的关键课题，是网络优化问题的一个重要分支。在复杂的网络中寻找最优路径，能够有效提高网络数据的传输性能，从而为用户提供更好的QoS保障［1］。最短路径问题已经有了很长的研究历史，且算法理论也在不断取得进步，著名的最短路径算法有Di⁃jkstra 算法［2］、Bellman-Ford 算法［3］、Floyd 算法［4～5］、SPFA 算法［6］等。

带宽（Bandwidth）和开销（cost）是衡量网络中一条通道性能的重要指标。带宽是指在单位时间内能传输的数据量。开销是指对网络进行路由管理而产生的代价的度量信息，比如延迟、链路状况、跳数等。在网路选择中，人们希望获得的路径开销更小而带宽更大，但在路由计算时，却往往将两者分开来考虑。现在针对于最优路径的研究，大多是以这两个中的某一个作为参量来进行计算的。文献［1］从保证通道带宽入手，研究了基于端到端的最优化流量控制。文献［8］提出的寻找最大带宽路径对算法同样是以带宽作为选路的依据。文献［9～11］则是以寻求最小的开销作为目标，研究了适应于实际需求的Dijkstra算法优化策略。多参数约束的路由问题大多数都是NPC（NP-Complete）问题，文献［12］指出带宽和延迟、代价、延迟抖动、丢失率之一结合的两参数路由问题是多参数路由中仅有的非NPC问题。

一条路径的带宽决定了吞吐量的大小，开销决定了数据流传输的时延。单纯以最小开销或最大带宽作为依据而构建的路径往往不是最优路径。最短路径开销最小却难以获得最大带宽，而带宽最大路径又不能保证开销最小，这都会成为数据流在这条路径上传输性能的短板。为了使所选路径具有最佳传输性能，本文兼顾带宽和开销，对经典的Dijkstra算法进行了合理化改进。

2 算法设计

2.1 Dijkstra算法介绍

Dijkstra算法是求单源最短路径的经典算法［13］。它采用标记法按照路径长度递增的顺序寻找最短路径，首先从源点开始，找出长度最短的一条路径及节点，然后从新节点出发，通过迭代得到从源点到其余各节点的最短路径［9］。

Dijkstra算法的基本过程［14］如下：在整个网络中设置两个集合，集合T是经过计算加入到最短路径树中的节点，集合S是还未加入到最短路径树中的节点［9］。假设每个节点 vj都有一对参数 (dj，pj)，dj是从源节点vs到节点vj的最短路径长度，pj代表节点vj在最短路径中的父亲节点。

步骤一：初始化，T=∅，S包含了网络中的所有节点。设置所有节点dj=∞，pj=［.］。

步骤二：将源节点vs加入集合T，并从S中删除，设置ds=0，ps∈∅。

步骤三：检验集合T中的所有节点vi到的S中节点vj的距离lij，其中vi到vj必须是直接连接的，中间无其他节点。设置dj=min[dj，di+lij]。

步骤四：选取dj最小的节点vj，将其从集合S中删除，并加入到集合T中去，该节点成为最短路径树中的一个新节点。

步骤五：找到新节点vj的父亲节点 pj，并记录该节点的两个参数(dj，pj)。

步骤六：重复步骤三到步骤五的过程，直到网络中的所有节点全部加入到集合T中，此时集合S=∅，完成整个过程。

2.2 问题描述及参量设置

2.2.1 问题描述

假设存在图1所示的无向加权网络G=(V，E)，V表示G中节点的集合，E表示G中的边的集合，|V|=n，| E |=m。G中的节点用vi(i=1，2，3，…，n)来表示，图中已经给出了源节点vs和目的节点vt。如果两个节点之间有物理连接，则称这两个节点之间存在一条边，每条边eij=[vi，vj]存在一对参数，该边的开销 h(eij)和带宽 b(eij)，记为（h(eij)，b(eij)）。 G 中的一条路径表示为 P={v1，v2，v3，…，vr}，(r≤n)。定义路径P的开销为P中包含的所有边的和值；路径P的带宽为P中所有边带宽的最小值［15］。

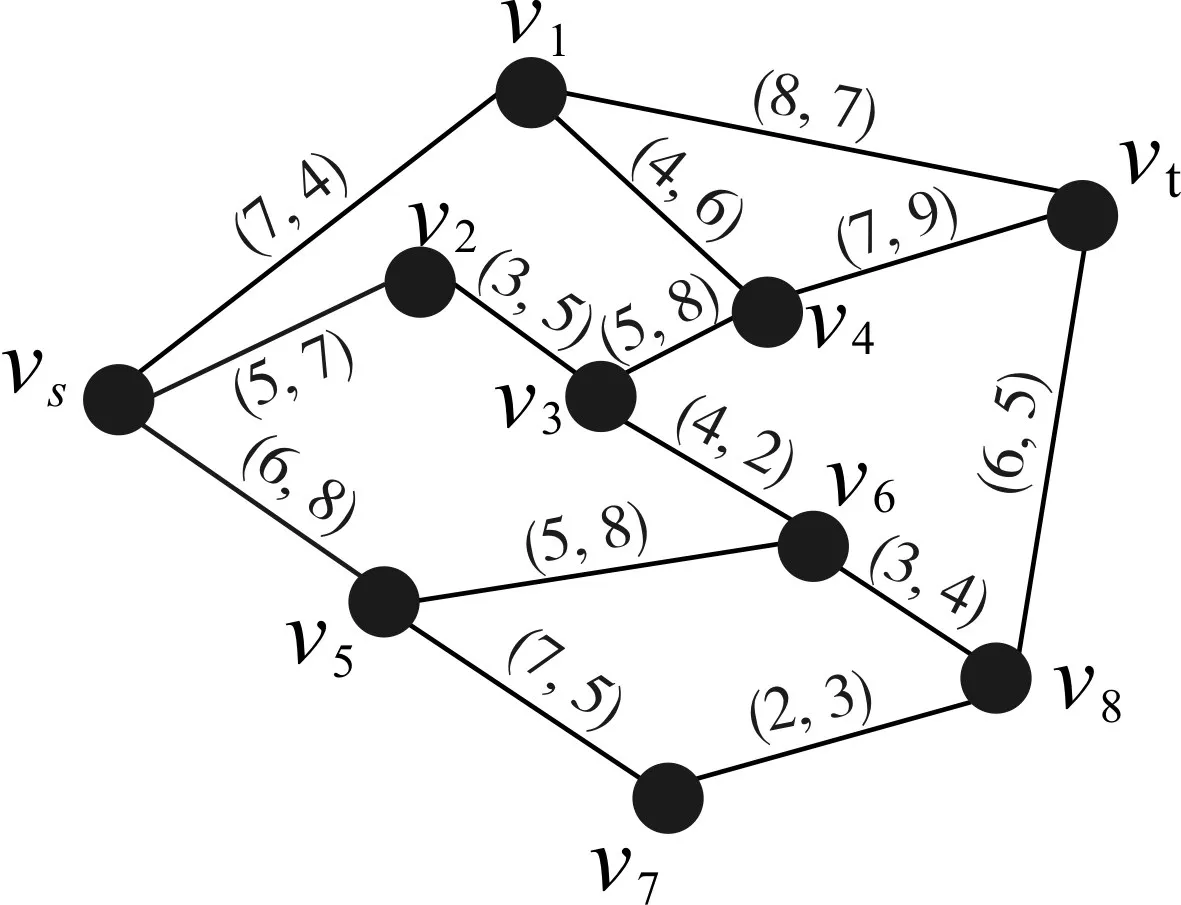
图1 加权网络图

使用Dijkstra算法在该网络中来寻找最短路径，仅仅利用了了每条边两个参数中的一个参数，即开销h(eij)，使得路径上的所有边的开销之和最小。使用Dijkstra算法解算出的最短路径树如图2所示，源节点vs到树中的任意节点都有唯一一条最短路径，当然指定的目的节点vt到源节点vs的最短路径也就找到了。

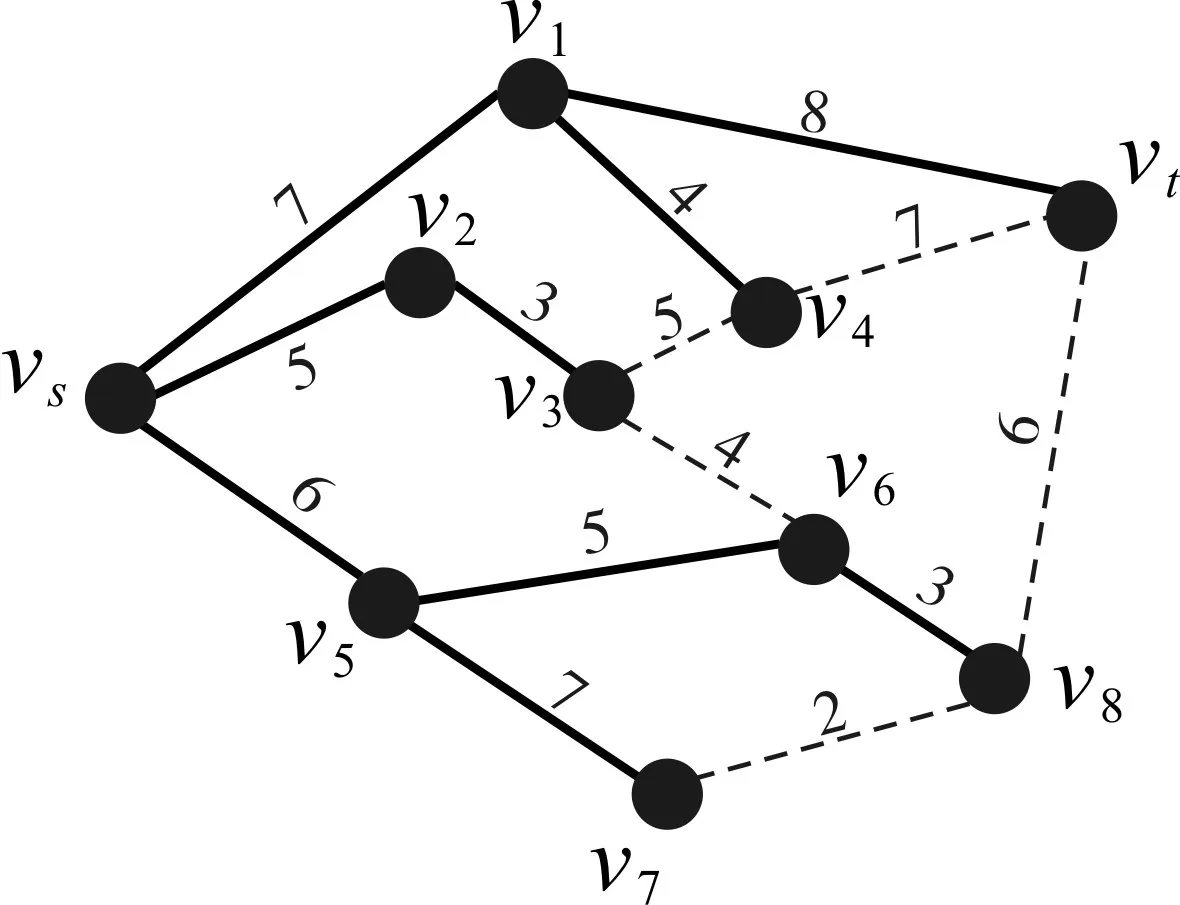
图2 使用Dijkstra算法计算的最短路径树

表1显示了从vs到vt所有可能路径的带宽，从表中可以看出，Dijkstra算法找出的最短路径P={vs，v1，vt}虽然开销最小，但它的带宽不是所有路径中最大的。带宽最大的路径是第2、第3条路径，但是它的开销也不是最小的。仅以一个参量作为选路依据，难免会使另一个参量成为制约通道性能的制约因素，成为数据传输的“瓶颈”。因此需要一个更加合理的参量，能够兼顾带宽和开销两个参量，综合性地描述一条边的性能。依据新的参量计算出的路径，可能不是开销最小的，也不是带宽最大的，但是能使其传输性能在网络中更加优化。

表1 vs到vt所有可能路径的带宽

2.2.2 参量设置

按照上节中对新参量的期望，我们进行如下定义：

定义1 加权无向网络G=(V，E)中两个节点形成的边eij=[vi，vj]含有带宽和开销两个参数，把开销和带宽的比值称为这条边的优秀值，即

f(eij)反映了一条边的质量的好坏。带宽和开销在选路中是两个互相矛盾的参量。我们在选择路径时总是希望一条边的带宽越大越好，开销越小越好，f(eij)值越小，说明这条边的质量越好，在路径计算时选择这条边的概率就越大［16］。为了使带宽和开销在数值上具有可比性，对两个参量进行归一化处理。用 h(eij)/∑h(eij)来代替 h(eij)，用h(eij)/∑h(eij)来代替b(eij)，其中∑h(eij)表示网络G中所有的边开销的总和，∑b(eij)表示网络G中所有的边带宽的总和。归一化消除了两个参量单位上的不统一，f(eij)成为一个只有数值没有单位的参量，它的表达式变成

2.3 算法实现

该算法是在Dijkstra最短路径算法的基础上，以边的“优秀值”作为新的度量，寻找源节点vs到目的节点vt的“度量最小的路径”［17］。算法过程分为三个阶段。

第一阶段：进行初始化操作。根据网络G中边的参数 (h(eij)，b(eij))以及公式 f(eij)=计算出每条边的“优秀值”作为寻路的新的度量。

第二阶段：构建“最优路径树”，实质上是对Di⁃jkstra最短路径算法的改进。将网络G中所有节点分为两个集合T和S。T是最优路径树中的节点集合，S是待判断的节点集合。对于已经加入到树T 中的节点 vj赋予3个参数 (dj，bj，pj)，dj是从源节点vs到节点vj的最短路径开销，bj是源节点vs到节点vj所形成路径的带宽，pj代表节点vj在最短路径中的父亲节点。每一次迭代过程都寻找当前节点vr到源节点vs的最优路径，并将vr添加到树中，记录vr的3个参数，直到所有节点或目的节点被包含到“最优路径树”当中为止。

第三阶段：路径建立过程。“最优路径树”计算完成后，所有节点3个参数(dj，bj，pj)都被记录了下来。利用这些参数，反向寻找某一节点的父亲节点，能够从目的节点vt反向一步一步构建起到起点节点vs的路径，并且获知该路径的开销带宽信息［18］。算法1详细描述了该算法的实现过程：

算法1

Input：网络G，源节点vs和目的节点vt；

Output：从vs到vt的最优路径 P

1.for alle∈Edo

2.计算 f(e)=(h ( e)/∑h(e))/(b ( e)/∑b(e))

3.end for

4.for allv∈Vdo

5. d(v)=∞，b(v)=-∞，p(v)=[.]

6.end for

7.addvstoT ，d(vs)=0，b(vs)=∞，p(vs)=0，f(ess)=0

8.do｛

9. for allvi∈Tdo

10. for allvj∈Sdo

11. 计算 f(esj)=f(esi)+f(eij)

12. f(esk)=min[f(esj)]

13. d(vk)=d(vi)+h(eik) ， b(vk)=min[b(vi)，b(eik)] ，p(vk)=vi

14. addvktoT，i=k

15. end for

16. end for

17.｝while(T=V or vs∈ T)

18.addvttoP

19.whilevt≠vsdo

20. p(vt)=vr

21. adderttoP

22. vt=vr

23.end while

根据新的度量值计算形成的最优路径树如图3所示，与图2所示的根据开销计算的最短路径树结果有所不同。由图2得到的最短路径是[vs，v1，vt]，开销值为15，路径的最大带宽值为4；由图 3 得到的最优路径是 [vs，v2，v3，v4，vt]，开销值为20，路径最大带宽为5。使用优化之后的算法得到的路径开销虽然不是最小，但是在路径的最大带宽上较之前相比有提升。虽然这个例子只是为了说明算法优化之后的运算效果，节点数目比较少难免可能出现路径开销和最大带宽都降低的极端情况。但在实际网络中，当节点数目达到一定数量的时候，才能够统计意义上来讲，优化后的算法能够达到开销和带宽的平衡。

图3 最优路径树

3 实验验证

为了证明本文提出的改进算法的正确性，用程序代码分别实现了3个算法。生成N个点作为网络节点，N取［100，1000］，取样间隔为100。以矩阵的形式表示各节点之间的连接关系以及开销、带宽两个参数，用两个矩阵来描述一个网络。矩阵一，描述开销，随机生成［30，80］中的任意数值，有数值代表两个节点之间有连接，两个节点之间没有连接则数值为无穷大（实际上就是系统最大值）；矩阵二，描述带宽，与开销矩阵所表示的节点连接关系一一对应，带宽值随机生成［15，85］中的任意值，两个节点之间没有连接的带宽值为0。在网络中指定源节点vs和目的节点vt，用3种算法分别计算出对应路径，统计在不同节点数目下3中算法运行完成所需要的时间以及获得路径的开销和带宽值，以此来比较3种算法的性能。

图4 3种算法的模拟测试结果

从实验结果中来看，图3（a）显示3种算法的运行时间相当，这是因为3种算法的核心都是Dijkstra算法，具有相同的时间复杂度，因此实验结果与预期是相符的。图3（b）比较的是3种算法计算出的路径的开销状况，最小开销算法以开销作为选路依据，所以路径的开销值能够维持在一个比较小的水平上；兼顾带宽和开销算法以最小开销算法作为蓝本，融入了带宽因素，与最小开销算法数值相当；最大带宽算法目的是获得最大带宽路径，完全不考虑开销的影响，因此所计算出的路径开销最大。图3（c）比较的是三种算法计算出的路径的带宽状况，最大带宽算法以带宽作为选路依据，计算出的路径具有最大带宽，相比之下最小开销算法和兼顾算法计算的路径带宽值较小，但是就整体趋势而言，兼顾算法所得带宽仍比只以获得最小开销的算法获得的带宽大，由此证明引入带宽因素提高了算法性能。兼顾带宽和开销的最优路径算法相比其他两种算法而言是具有一定优势的。

4 结语

关于路由算法的研究大多是以路径的开销或带宽作为考察依据的，但是选路中无论是以开销优先还是带宽优先，都会造成对另一个参数的忽略，难以获得最“优”的路径。路径的开销和带宽都影响着网络数据的传输性能，因此我们更希望算法能够计算出开销和带宽都比较好的路径。

本文以上述观点作为指导思想，研究了一种能够兼顾带宽和开销的路由算法。选择路由算法中经典的Dijkstra算法作为改进的对象，对权值进行重新定义，以开销和带宽的比值作为新的权值，再用Dijkstra算法计算出权值最小的路径。通过理论研究和实验验证，证明了改进后的算法在时间复杂度上与传统算法相当，在保证开销仍然较小的情况下，带宽性能有所提高。这一研究对于多因素影响的路由问题提供了一种解决思想，对于平衡多种选路参量，获得最佳网络传输性能具有重要意义。