考虑鼓胀变形影响的散体材料桩单桩极限承载力修正计算

陈君炜，谭 鑫

(1.广西交通投资集团柳州高速公路运营有限公司，广西 柳州 545000；2.湖南大学，湖南 长沙 410082)

0 引言

散体材料桩复合地基能够有效提高地基承载力，增强其稳定性，控制沉降，且施工简便、快速，工程造价较低，是适合我国国情的一种人工地基。散体材料桩复合地基承载力的提高，除取决于散体材料桩的数量布置外，还取决于散体材料桩桩体自身的承载力。绝大多数散体材料桩承载力的丧失是由于散体材料的径向鼓胀变形持续发展所导致。怎样合理地计算散体材料桩桩周土体所能够提供的极限侧向土压力是其承载力计算的关键问题，而现有的计算方法没有考虑到桩体鼓胀变形模式对桩周土体极限侧向土压力的影响，与工程实测比较仍存在较大的误差。

1 弧形墙面计算模型与分析方法

1.1 基本假设

采用数值方法对散体材料桩鼓胀变形模式的桩侧土体极限侧向约束力进行分析研究，由于对埋入土体内的散体材料桩缺乏精密而有效的测量方法，散体材料桩鼓胀变形的测试结果文献中记录并不丰富。本文从文献中选取了一些典型的散体材料桩单桩模型试验的鼓胀变形测量结果，并将鼓胀变形无量纲化后描绘在图1(a)中，鼓胀变形用桩身的侧向应变(εr=Δr/r)表示。从单桩丧失承载力后的鼓胀变形轮廓看出，大部分桩体鼓胀发生在桩体上部2～2.5倍桩径范围内，最大侧向变形通常发生在鼓胀段中部，破坏时最大径向应变在20%以内(0.1倍桩径)，鼓胀轮廓多呈现中间大两端小的外凸弧形模式。

(a)假设鼓胀轮廓形状

(b) 数值计算模型

1.2 建立数值计算模型

根据无量纲后的鼓胀轮廓线，将最终鼓胀变形简化假设成一段圆弧(图1a中的虚线)，圆弧半径为3倍桩径，圆弧高度为2倍桩径。圆弧中部凸出部位为最大鼓胀径向应变对应的侧向变形，即0.1倍桩径。建立数值模型尺寸为4d×6d(d=1 m)，模型及边界条件见图1(b)，鼓胀变形通过在鼓胀变形段网格节点赋予水平方向的速度，沿竖向分布，大小采用图1鼓胀变形分布形状。土体采用摩尔库伦本构模型，变形模量取E=1 MPa，ν=0.35，强度参数分别取粘聚力c为7.5 kPa、10 kPa、12.5 kPa，内摩擦角φ为7.5°、10°、12.5°。数值计算过程中记录鼓胀段变形过程中受到的来自土体的侧向土压力，并与Rankine被动土压力理论计算值进行对比分析。

2 数值分析结果

鼓胀变形最大处的土体侧向应力随侧向应变的发展曲线见图2。由于采用同样的变形模量，不同强度参数的应力应变曲线在初始加载段线性上升，随着部分土体单元发生塑性屈服，曲线偏离线性阶段，当塑性区域逐渐扩大并贯通至地表，侧向应力达到极限值，极限值随强度参数提高而提高。土体在鼓胀变形发展下(图2中a、b、c阶段)的破坏过程见图3。

图2 鼓胀变形最大处土体侧向应力发展曲线图

图3 不同鼓胀变形阶段土体侧向应力分布曲线图

从塑性区发展过程上看[图4(a)]，随着鼓胀变形的发展，塑性区从鼓胀段下端开始产生，然后逐渐向上发展直至最终贯通地表形成整体剪切破坏区域，但是对比Rankine被动土压力的极限平衡滑动面，弧形鼓胀模式产生的塑性区面积远大于Rankine被动土压力的假设；最大剪应变云图[图4(c)]也说明了这一点，土体产生剪切变形的区域远大于Rnakine被动土压力理论中滑移面包围的区域，往更深更广的区域发展。土体侧向应力分布如图4(b)所示，靠近鼓胀段中部的土体侧向应力随径向应变增长而迅速增长，并最先达到极值，最终鼓胀中下段的侧向应力也都将达到极值。

(a)塑性区发展

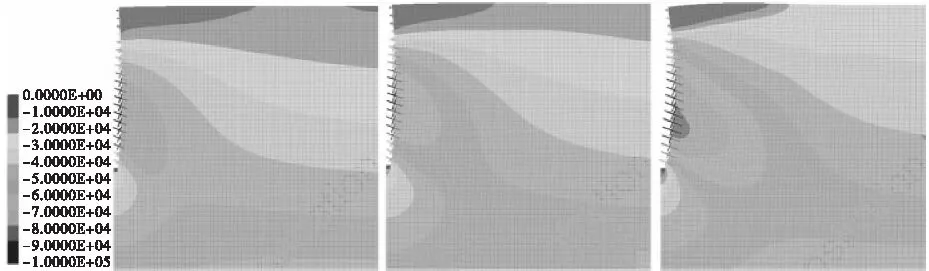
(b)土体水平应力发展

(c)剪切应变发展

将不同侧向应变下侧向应力沿整个鼓胀变形段的分布曲线提取出来(见图3)，在鼓胀初始阶段(εr=1%)侧向应力分布随深度增加；随着鼓胀变形继续发展，鼓胀段中部侧向应力增加迅速，而鼓胀段两端应力增长较缓慢，当径向应变发展到εr=5%时(对应于图2中a点)，鼓胀段中部侧向应力就已经超过了Rankine被动土压力在该段的计算值；侧向应力分布呈中间大、两端小的抛物线型(εr为5%和7%时)，抛物线最大值越来越突出，且有往深处移动的趋势；直到径向应变发展到εr>10%以后，侧向应力基本达到极限值不再增加，此时土体的极限侧向应力较Rankine被动土压力计算值有较大程度的提高，这在鼓胀端中部表现得尤为明显。

3 参数分析

在不同强度参数下，土体极限侧压力分布与Rankine被动土压力分布和鼓胀段被动土压力分布的形式类似(见图5)，但鼓胀变形计算值较Rankine计算值均有所增加，增加的幅度随着强度参数产生变化。选取不同强度参数进行计算，粘聚力c取0～60 kPa，内摩擦角φ取0°～25°。为了便于与Rankine被动土压力进行比较，定义了一个侧土压力比，为数值计算中鼓胀段中点土体极限侧向应力与同深度Rankine被动土压力的比值。且为了不至于高估土体极限侧向应力，应力值均选取在土体整体剪切滑移区形成之前(见图2中b点)。该比例系数与强度参数的关系见图6、图7。

(a)粘聚力固定、内摩擦角不同条件下

(b)粘聚力不同、内摩擦角固定条件下

由图6、图7可见，由于鼓胀变形模式的影响，鼓胀段中部受到来自周围土体的极限侧向应力始终大于Rankine被动土压力强度在该深度的计算值，故侧土压力比始终>1。比值随粘聚力c、内摩擦角φ值的增大而增大，但增大的幅度与c、φ取值范围有关。在摩擦角<25°范围内，侧土压力比大致随着摩擦角线性增大(见图5)。在粘聚力<20 kPa范围内，侧土压力比随粘聚力增大；在粘聚力>20 kPa但<60 kPa的范围内，侧土压力比随粘聚力增大幅度不明显(见图7)。

图6 侧土压力比随土体内摩擦角变化图

图7 侧土压力比随土体粘聚力变化图

根据图6、图7计算得到的结果，并考虑到软土摩擦角一般取值较小而粘聚力变化范围较大，所以重点分析侧土压力比随粘聚力的变化关系。选取指数函数对侧土应力比随粘聚力的变化关系进行拟合，拟合关系式为：

y=1+y0-0.14e(-0.1cu)

(1)

图8 系数y0的拟合关系式示意图

其中y0为不同摩擦角对应的拟合参数，该参数代表侧土应力比与摩擦角的线性关系。将y0与摩擦角正切值的关系表述在图8中。两段式线性拟合能够很好地表示两者的关系：

y0=0.5tanφ+0.3(φ≤10°)

y0=0.2tanφ+0.36(φ>10°)

(2)

综上，鼓胀变形模式的土体极限侧向约束力可以利用上述侧土压力比在Rankine被动土压力式(5)的基础上进行修正，修正公式为：

(3)

则散体材料桩单桩极限承载力公式采用如下修正形式：

(4)

其中

(5)

设某场地软土重度γs=18 kN/m3、散体材料桩直径d=1.0 m、碎石内摩擦角φp=38°。不同计算方法计算得到的碎石桩单桩极限承载力结果对比见图9。

图9 不同单桩承载力计算结果比较图

本文提出的修正方法仍采用摩尔库伦强度参数进行修正，便于工程应用。由于考虑鼓胀变形模式带来土体极限侧向约束力的增加，修正后的散体材料桩单桩极限承载力与被动土压力法相比在低剪切强度(<20 kPa)桩周土情况下降低，而在高剪切强度(>20 kPa)桩周土情况下增加；与Brauns和Hughes & Withers相比在低剪切强度(<20 kPa)桩周土情况下增加，而在高剪切强度(>20 kPa)桩周土情况下降低，更接近工程实践观测到的结果，并且土体极限侧向约束力取至鼓胀段中部鼓胀变形最剧烈处，比修正前更符合散体材料桩鼓胀破坏的机理。

4 结语

散体材料桩单桩极限承载力计算中对桩周土体提供的极限侧向土压力缺乏正确的计算方法，无法考虑到桩体鼓胀变形模式对其侧向土压力大小及分布的影响，与散体材料桩鼓胀破坏的模式不尽符合。本文从典型散体材料桩单桩模型试验的鼓胀变形测量结果入手，以数值模拟揭示随着鼓胀变形的发展，桩周土体侧向土压力的变化及分布，并通过相关参数分析，在被动土压力方法的基础上对散体材料桩单桩极限承载力公式进行了修正。修正后的散体材料桩单桩极限承载力公式更接近工程实践观测到的结果，且更符合散体材料桩鼓胀破坏机理。