固体火箭发动机破片冲击起爆阈值计算①

2018-11-26徐秉恒郭运强

固体火箭技术 2018年5期

杨琨，徐秉恒，郭运强，吴秋

(中国航天科技集团公司四院四十一所，西安 710025)

0 引言

固体火箭发动机作为导弹武器的动力装置，一旦发生危险，会对周围的人和物造成巨大的伤害。20世纪60年代，美国海军军事装备频频出现意外。例如，1967年福莱斯特(Forrestal-class aircraft carriers)和1969年美国企业号(USS Enterprise)航空母舰上的弹药意外，都造成了严重的人员伤亡和财物损失。随之，美国海军逐渐开始重视弹药的安全性，并联合美国空军和陆军以及北约有关国家制定了一系列的弹药安全性标准[1-3]。

随着国内武器弹药的高能化需求，弹药的安全性问题也越来越突出，引起了相关单位和专家的重视，出台了《固体推进剂快速烤燃试验方法》 (QJ 20153—2012)、《固体推进剂慢速烤燃试验方法》(QJ 20152—2012)和《空-空导弹最低安全要求》(GJB 357—87)等标准。目前，主要的安全性试验有快速烤燃、慢速烤燃、破片冲击、子弹冲击、殉爆和聚能射流等[4-5]。

本文采用试验加数值模拟的方法，对固体火箭发动机的破片冲击安全性进行研究。对某型号固体火箭发动机进行破片冲击试验。试验证明，m=19.18×10-3kg、d=40 mm的破片以v=2375 m/s的速度冲击某型号固体火箭发动机引起爆燃。简化破片冲击某型号固体火箭发动机模型，采用非线性有限元动力学ANSYS/LS-DYNA软件，对破片冲击某型号固体火箭发动机过程进行数值模拟，并分析影响破片冲击固体火箭发动机起爆阈值的因素，为固体火箭发动机安全性设计提供借鉴。

1 破片冲击固体火箭发动机试验

1.1 试验过程

图1为试验用发动机结构简图和试验布置示意图。破片发射器发射高速破片，冲击发动机，用超压传感器和验证板确定发动机反应级别。表1为破片和发动机参数。图2为试验用破片示意图，表2为试验破片规格。图3为破片冲击发动机响应瞬间，破片冲击发动机后产生明显的响声，并能观察到飞散的火球。

(a)发动机简图

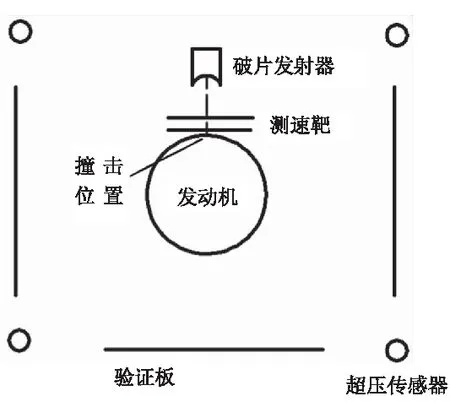
(b)试验布置示意图

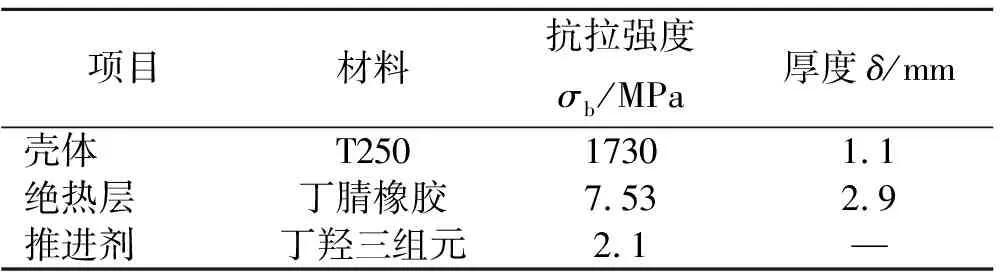
项目材料抗拉强度σb/MPa厚度δ/mm壳体T25017301.1绝热层丁腈橡胶7.532.9推进剂丁羟三组元2.1—

表2 破片规格参数

(a)俯视图 (b)侧视图

(a)冲击起爆 (b)剧烈燃烧

1.2 试验结果

图4是试验后壳体复原图，发动机中间部分破碎，最大破损长度700 mm，两端部分保留在工装上，收集到4块发动机壳体碎片。

图4 试验后壳体复原图

表3为破片冲击固体火箭发动机试验结果与爆燃反应等级评判依据的比对。

根据反应等级评判依据，反应现象与爆燃等级评判依据一致，判定破片冲击某型号固体火箭发动机的反应等级为爆燃。

综上所述，质量为19.18×10-3kg、直径为40 mm的破片，以v=2375 m/s的速度冲击某型号固体火箭发动机，推进剂被起爆。

2 破片冲击固体火箭发动机数值模拟

试验很难得到破片冲击发动机时推进剂的反应过程。因此，利用有限元软件ANSYS/LS-DYNA，对上述破片冲击固体火箭发动机试验进行模拟，计算破片冲击起爆推进剂的反应过程。

表3 破片冲击试验结果与爆燃反应等级评判依据比对

2.1 材料模型及验证

2.1.1 材料模型

固体推进剂作为含能材料，具有和炸药相似的爆炸性能。因此，计算推进剂在破片冲击下的起爆响应，推进剂模型用点火增长反应模型和和JWL状态方程[6-8]，通过查看推进剂内部连续单元的压力升降来判断推进剂是否起爆，压力升高，推进剂起爆，压力降低，则推进剂未起爆。

点火增长反应模型方程形式为

G2(1-F)eFgpz

(1)

式中F是反应率，p为压力，μ为压缩冲程，I、G1、G2、a、b、c、d、x、y、e、g和z均为常数。

式(1)表示的点火与增长过程为三项式点火与增长模型，第一项表示部分推进剂在冲击压缩下点火，第二项表示推进剂快速反应产生爆轰气体的过程，第三项为反应后相对缓慢的扩散控制。其中，a是临界压缩度，当压缩度小于a时推进剂不能被点火，y定义燃烧项的压强指数，点火和燃烧项的燃耗阶数b=c=2/3，表示向内的球形颗粒燃烧，I和x控制点火热点的数量，G1和d控制了点火后热点早期的反应生长持续时间的函数，G2和z确定了高压下的反应速率。根据文献[9]，推进剂点火增长反应模型参数如下：I=7.4×1011、G1=7、G2=800、a=0、b=0.667、c=0.667、d=0.111、x=800，y=1.5、e=0.333、g=1.0、z=2.0。爆轰产物的JWL方程为

(2)

式中p为爆轰产物的压力；V为爆轰产物的相对比容；A、B、R1、R2、ω和E为待定参数，可通过圆管试验来标定。

冲击试验的应变率范围为102～104s-1，远高于准静态试验应变率。应变率的提高，使得材料的屈服极限、强度极限提高，延伸率下降、屈服滞后和断裂滞后等[10]。Johnson-Cook模型适用于大应变和高应变率计算，其表达式为

(3)

式中ερ为有效应变；ερ*为应变率；TH= (T-Troom)/(Tmelt-Troom)；A、B、C、n和m为常数。

上述试验破片为10#钢、壳体为T250钢，力学性能见表1和表2。由于该型号钢缺少Johnson-Cook模型参数，本文选用ANSYS材料库中与上述两种材料力学性能相近的低碳钢steel 1006和超高强度钢steel S-7进行替代，表4列出了2种钢材料以及后续计算要用到铝合金的Johnson-Cook模型材料参数。

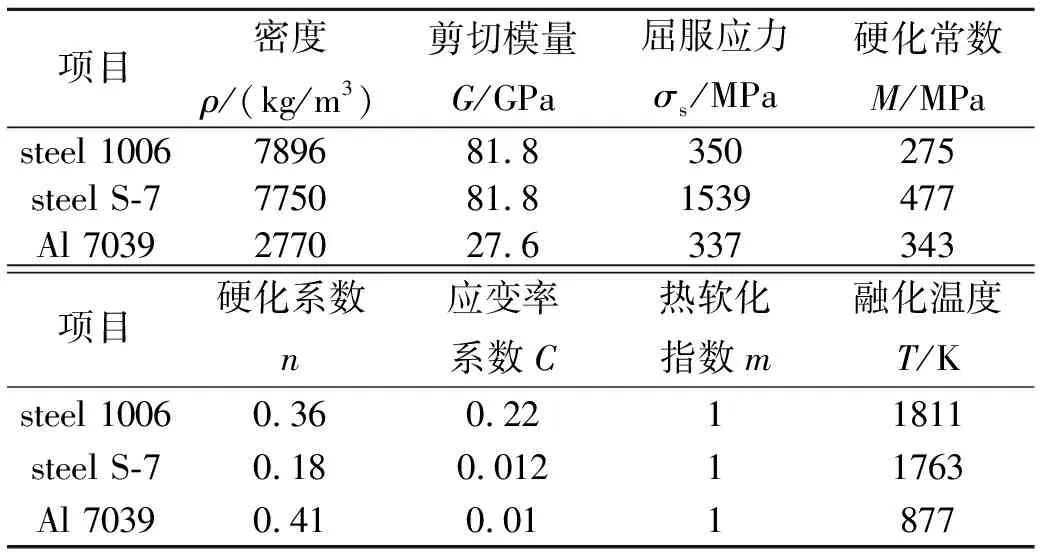
表4 Johnson-Cook模型材料参数

根据文献，对于采用橡胶材料的绝热层，材料模型用双线性弹塑性模型[11]，即用两条斜率不同的线段表示材料的应力-应变曲线，其表达式为

(4)

式中E为弹性模量；E1为切线模型，取值范围为0～E；σs为屈服应力；εs为屈服应变。

橡胶材料参数为密度ρ=1000 kg/m3，弹性模量E=1 MPa，切线模量取E1=1/2E，泊松比μ=0.49。

2.1.2 推进剂材料模型验证

文献[8]中利用拉氏分析试验，对固体推进剂冲击起爆特性进行研究，试验过程为雷管引爆炸药透镜，炸药透镜产生平面冲击波作用加载药柱起爆，通过铝隔板衰减后的冲击波作用于推进剂，试验测得推进剂不同位置的压力值。本部分对该试验进行数值模拟，计算推进剂不同位置压力值，与试验结果进行比对，以验证后续计算用材料模型的准确性。

图5为试验装置图和数值模拟模型。其中，TNT炸药直径80 mm，厚度10 mm；铝隔板直径100 mm，厚度50 mm；推进剂直径50 mm。数值模拟模型为“准二维”对称模型，TNT炸药起爆方式为面起爆。

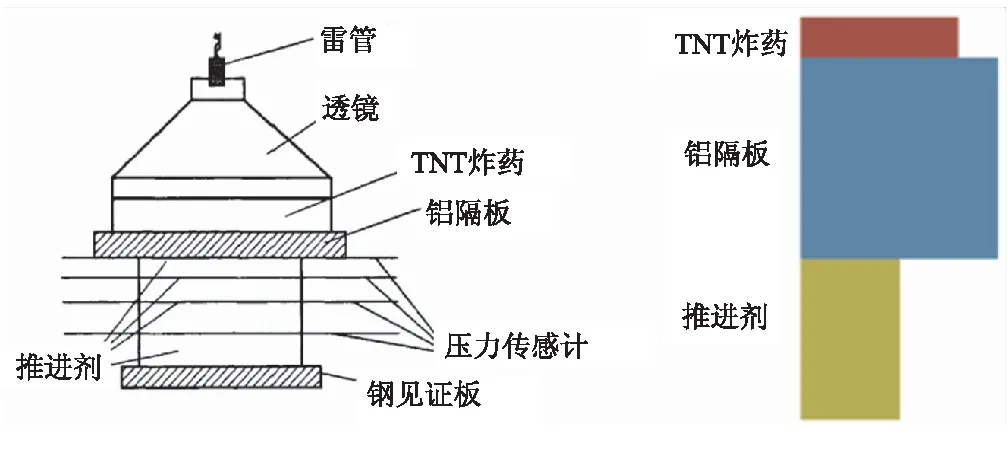
(a)拉氏试验装置 (b)数值模拟模型

表5将计算得到的压力值与试验测得压力值和文献中数值模拟得到的压力值进行对比。从表5可看出，本文采取的推进剂材料模型能很好地计算推进剂起爆过程。

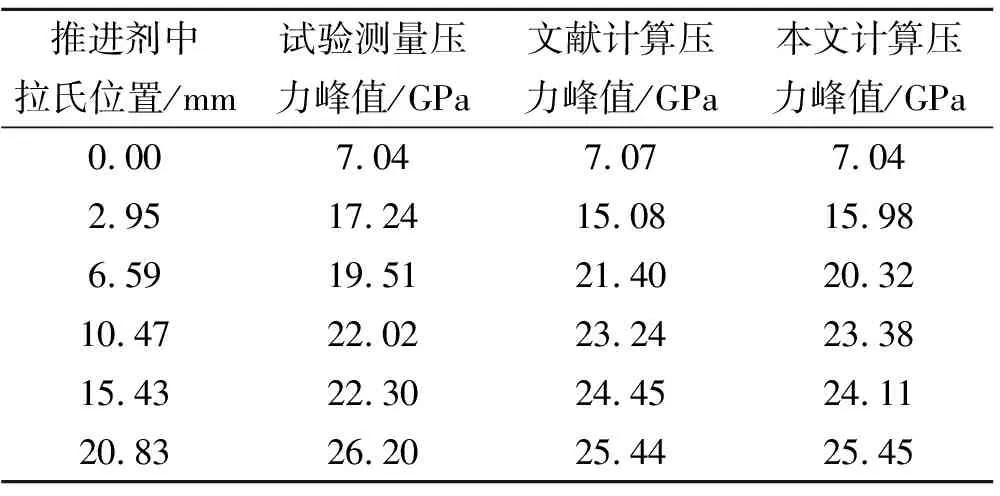
表5 计算测点压力值与文献试验、计算压力值的比较

2.2 破片冲击固体火箭发动机结构模型

固体火箭发动机结构主要包括壳体、绝热层和推进剂。由于破片体积相对于固体火箭发动机很小，且破片冲击发动机的影响区域有限，对破片冲击固体火箭发动机的模型进行简化，考虑对称性，建立1/4模型进行计算，对上述试验简化后的模型如图6所示。破片、壳体、绝热层和推进剂之间定义侵蚀接触算法，壳体、绝热层和推进剂边界定义非反射边界。

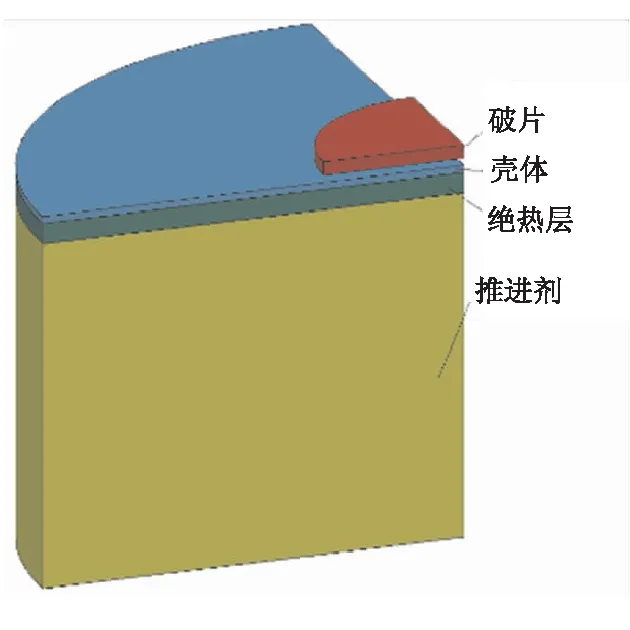
图6 破片冲击固体火箭发动机简化模型

2.3 计算结果

图7为破片冲击固体火箭发动机起爆过程，破片速度v=2375 m/s。

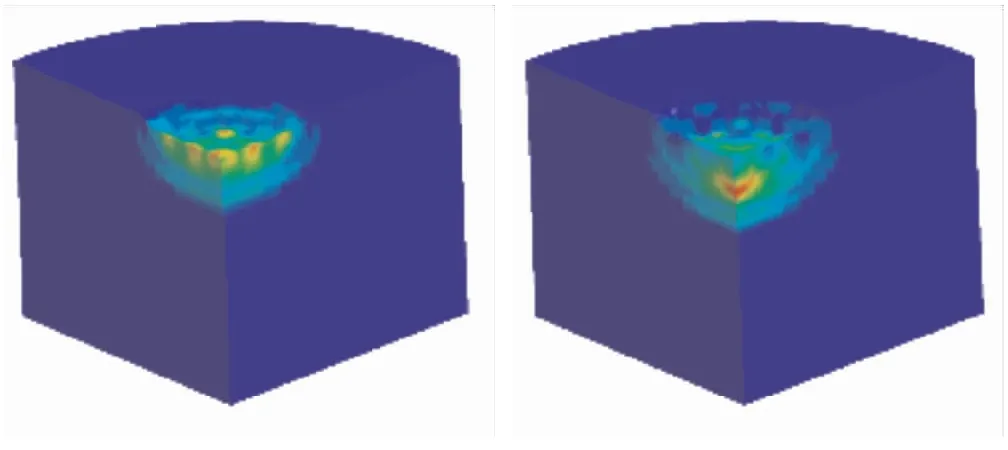
(a)t=5 μs (b)t=6 μs

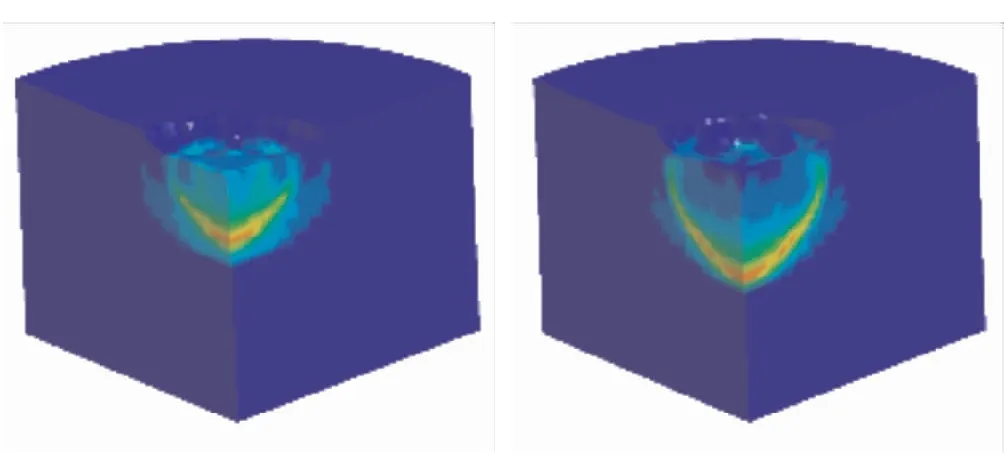
(c)t=7 μs (d)t=8 μs

由图7可看出，破片冲击发动机，在推进剂中形成高压区域，高压区域以球形面的方式迅速向外传播，点燃外部推进剂，从而引起推进剂爆炸。沿破片冲击发动机的方向选定推进剂内部连续单元，给出v=2375 m/s和v=1750 m/s的压力曲线，图8给出了选取的推进剂内部单元示意图和不同冲击速度下单元的压力。

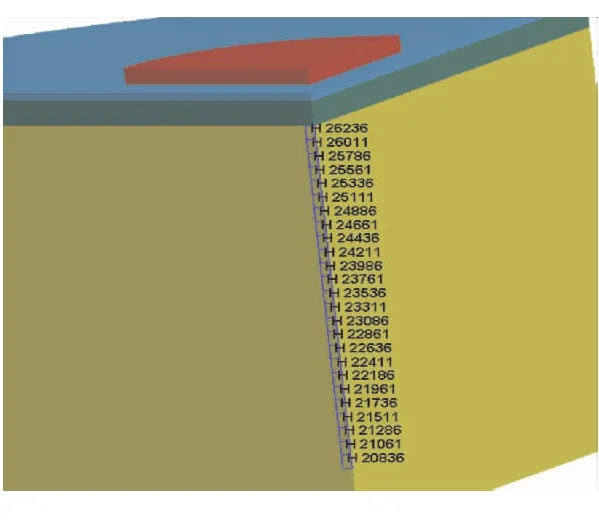
(a)推进剂内部单元选取示意图

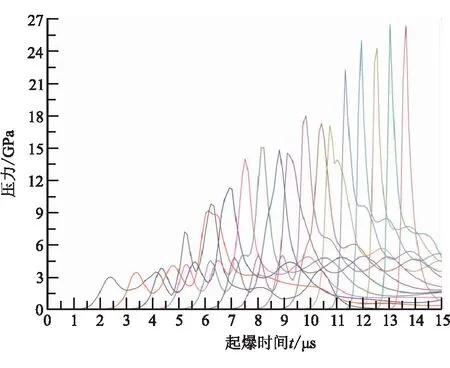
(b)v=2375 m/s单元内部压力

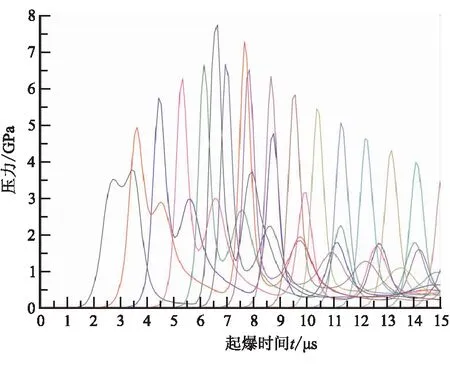
(c)v=1750 m/s单元内部压力

从图8可看出，破片速度v=2375 m/s，推进剂内部压力呈上升状态，最终达到稳定值，破片速度v=1750 m/s，内部压力先升高、后下降，说明破片速度v=2375 m/s时，推进剂起爆，破片速度v=1750 m/s时，推进剂未起爆。破片以v=2375 m/s的速度冲击发动机，推进剂压力开始较低，接着持续升高，最终达到一个稳定的阶段，分别对应燃烧阶段、快速反应阶段和爆轰阶段，初始燃烧阶段压力较低，为3～4 GPa，当压力达到7～8 GPa后，推进剂快速反应并最终达到稳定的爆轰阶段，爆轰压力在26～27 GPa之间，这与上述拉氏试验测到的爆轰压力一致。通过“升-降”法对该试验的起爆阈值进行计算，得到该工况下起爆阈值vcr=1781 m/s。

通过有限元方法，对上述破片冲击固体火箭发动机试验进行模拟。模拟结果显示，m=19.18×10-3kg、d=40 mm的破片，以v=2375 m/s的速度冲击某型号发动机能起爆推进剂，与试验结果相符。

3 破片冲击固体火箭发动机起爆阈值计算及影响因素

为了进一步分析影响破片冲击发动机起爆阈值的因素，利用上述数值模拟方法，计算不同工况下破片冲击发动机起爆阈值。

根据美军标MIL-STD-2105D和北约STANAG 4439钝感弹药评估和试验标准[2，12-13]，冲击发动机用破片规格为边长为12.7 mm的钢制立方体。采用“升-降”法，计算不同条件下破片冲击发动机起爆阈值，分析影响起爆阈值的因素。

3.1 不同壳体和绝热层厚度起爆阈值计算

分析壳体厚度和绝热层厚度对破片冲击发动机起爆阈值的影响。选择12.7 mm×12.7 mm×12.7 mm立方体破片，控制绝热层厚度δ=2 mm不变，以0.5 mm为步长，计算壳体厚度从2～5 mm破片冲击发动机起爆阈值。继续控制壳体厚度δ=2 mm不变，以0.5 mm的步长计算绝热层厚度从2～5 mm破片冲击发动机起爆阈值。破片和壳体材料均为高强度钢。图9为不同壳体和绝热层厚度工况下破片冲击发动机起爆阈值趋势图。

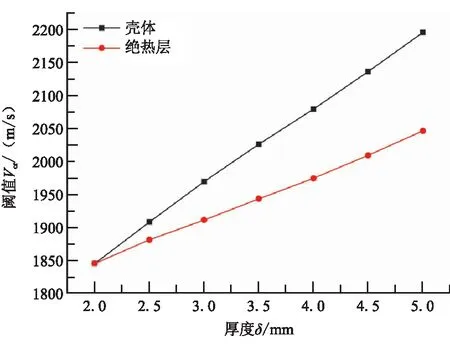
图9 不同壳体和绝热层厚度破片冲击发动机起爆阈值

壳体和绝热层厚度的增加，均使得破片冲击发动机的起爆阈值增加。壳体厚度从2 mm增加到5 mm，破片冲击发动机的起爆阈值近似线性增长，增长幅度约为120 m/(s·mm)。绝热层厚度从2 mm增加至5 mm，起爆阈值近似线性增长，增长幅度约为67 m/(s·mm)。

3.2 不同壳体材料起爆阈值计算

破片冲击发动机的工况之一是发生爆炸的发动机产生的破片对周围发动机的影响。依据实际情况，分析钢破片冲击钢壳体、钢破片冲击铝合金壳体和铝合金破片冲击铝合金壳体3种条件下起爆阈值变化。破片形状尺寸与上述一致，绝热层厚度不变，壳体厚度从2 mm增加至5 mm。图10为上述3种情况破片冲击发动机起爆阈值趋势图。

钢破片冲击铝合金壳体起爆阈值最低，铝合金破片冲击铝合金壳体起爆阈值最高。破片材料和壳体材料相同时，起爆阈值随壳体厚度增加近似线性增长，其中铝合金破片冲击铝合金壳体增幅为142 m/(s·mm)，钢破片冲击钢壳体增幅为120 m/(s·mm)。钢破片冲击铝合金壳体起爆阈值增幅随壳体厚度增加而增大。

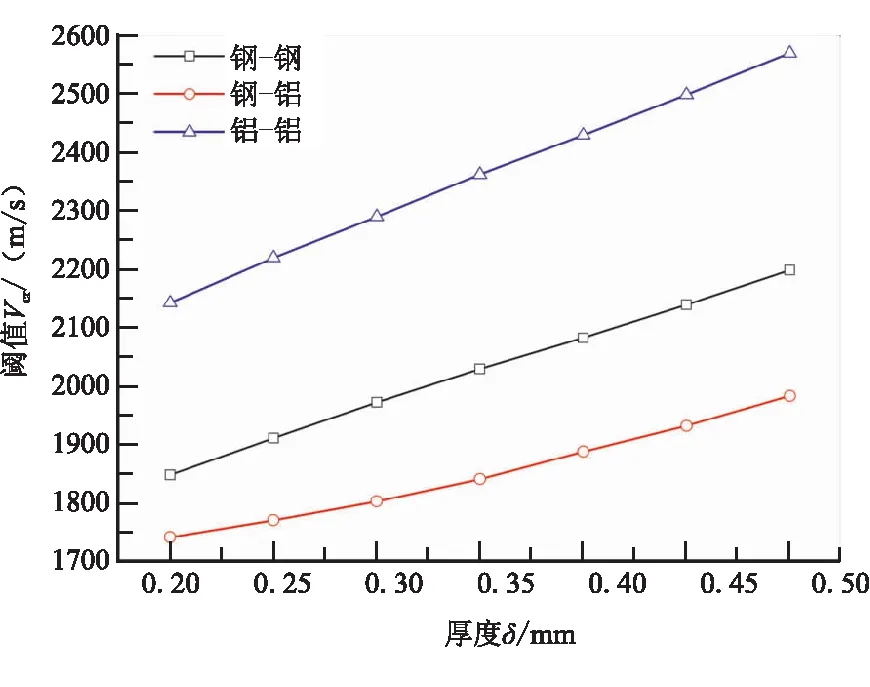
图10 不同壳体材料起爆阈值

3.3 不同破片形状起爆阈值计算

固体火箭发动机爆炸形成的破片形状是不规则的，一般将破片简化为球形破片、立方体破片和圆柱破片3种[14]。图11为3种破片冲击发动机示意图。壳体和破片材料均为高强度钢，控制绝热层厚度不变，3种破片质量相等，立方体破片和圆柱破片底面面积相等。计算随壳体厚度增加3种破片起爆阈值变化，立方体破片和平头圆柱破片以最大接触面积冲击发动机，图12为3种破片冲击发动机起爆阈值趋势图。

立方体破片和平头圆柱破片起爆阈值相近，随着壳体厚度增加，立方体破片起爆阈值略高于平头圆柱破片；球形破片起爆阈值远高于立方体破片和平头圆柱破片。3种破片起爆阈值都随壳体厚度增加近似线性增长，且增长幅度相近。

3.4 不同破片长宽比起爆阈值计算

保持射弹质量不变的情况下，改变射弹的长径比，引爆带壳炸药的起爆阈值速度也相应改变[15]。保持破片质量基本不变，定义长方体破片高度与底面边长之比H/L为长宽比，分析长方体破片长宽比对破片冲击发动机起爆阈值的影响。破片和壳体材料为高强度钢，图13为不同长宽比破片冲击发动机起爆阈值。可看出，破片冲击发动机起爆阈值随长宽比的增加呈非线性增长，增长幅度随长宽比增大有所减小。

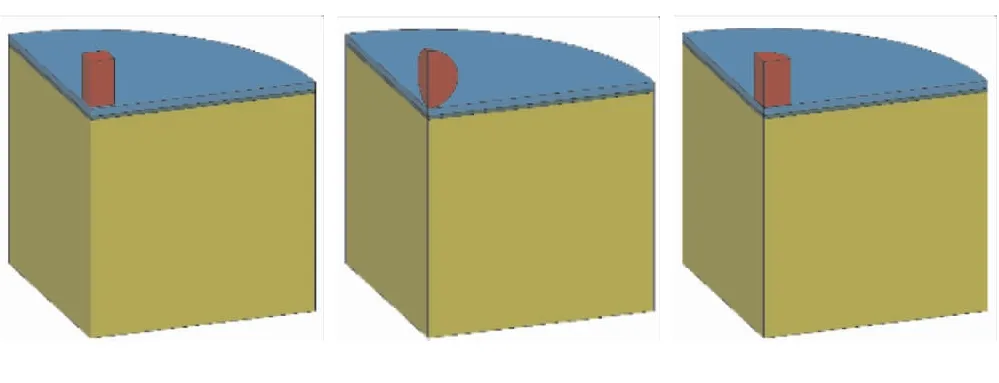
(a)立方体破片 (b)球形破片 (c)圆柱破片

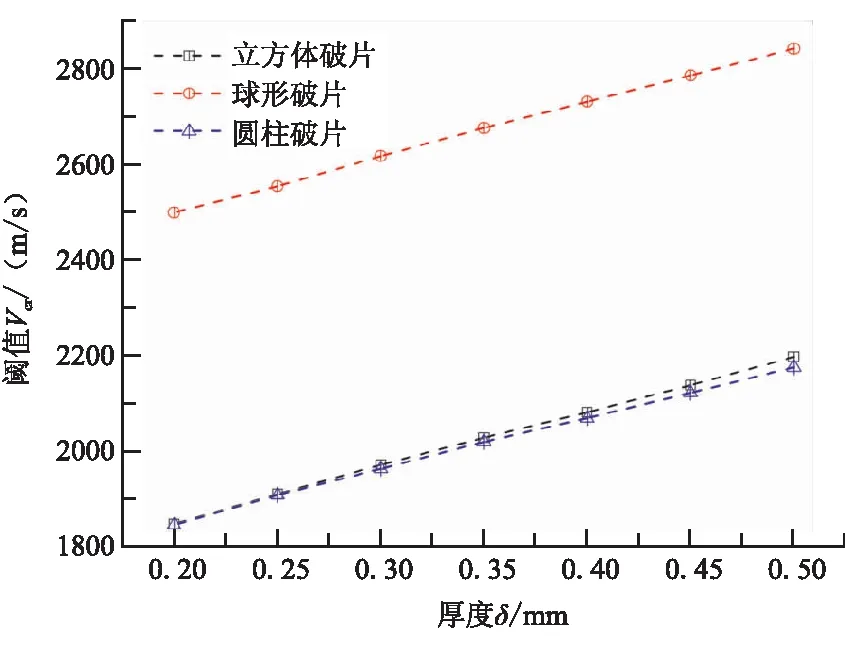
图12 3种破片冲击发动机起爆阈值

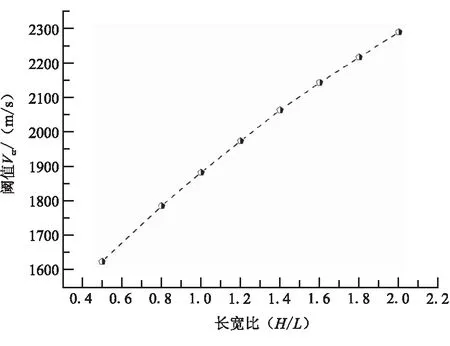
图13 不同长宽比破片冲击发动机起爆阈值

3.5 分析与讨论

从上述趋势图可看出，壳体厚度、绝热层厚度、壳体材料、破片材料、破片形状和长宽比等对破片冲击发动机起爆阈值都有不同程度影响。

由冲击理论可知，高速破片冲击发动机时，在破片和壳体内会形成两道强冲击波，冲击压力pc可用式(5)进行计算[10]：

(5)

式中pc为冲击产生的压力；ρp为破片的密度；Cp为破片的压缩波速；ρb为壳体的密度；Cb为壳体的压缩波速；v为破片的速度。

压缩波速的表达式为

(6)

式中E为材料的弹性模量；μ为材料泊松比；ρ为材料密度。

假设破片速度v=1800 m/s，利用上述理论计算得到钢破片冲击钢壳体、钢破片冲击铝合金壳体、铝合金破片冲击铝合金壳体产生的压力分别为42.39、23.13、15.90 GPa，数值模拟得到的压强分别为44.87、23.81、17.77 GPa，理论与数值模拟相符。破片与绝热层、破片与推进剂、绝热层与推进剂之间的冲击产生的压强，相比破片与壳体冲击产生的压强要小很多，可忽略。

冲击产生的压强以冲击波的形式在介质中传播，传播过程中会被稀疏，材料对冲击波的稀疏能力和材料的波阻抗(ρC)相关，波阻抗越大，稀疏能力越强。钢和铝合金的波阻抗分别为17.67×106kg/m3·m/s和47.10×106kg/m3·m/s，说明钢材料对冲击波的稀疏能力更强。

基于以上计算，对不同破片材料、壳体材料和壳体、绝热层厚度对破片冲击发动机起爆阈值的影响进行分析：

(1)数值模拟结果显示，壳体和绝热层厚度的增加，使破片冲击发动机起爆阈值升高，且增加相同厚度，壳体带来的起爆阈值升高更显著。这是因为壳体和绝热层厚度的增加会增加冲击波传播的距离，使得传递到推进剂的冲击波压强减小，而壳体材料的波阻抗大于绝热层材料的波阻抗。所以，壳体厚度的增加，对起爆阈值的提高更显著。

(2)相同壳体和绝热层厚度下，钢破片冲击铝合金壳体起爆阈值最低，铝合金破片冲击铝合金壳体起爆阈值最高。破片速度相等条件下，铝合金破片冲击铝合金壳体产生的冲击波压强最小，所以其起爆阈值最高；虽然钢破片冲击铝合金壳体产生的冲击波压强小于钢破片冲击钢壳体产生的冲击波压强，由于铝合金壳体的波阻抗小于钢壳体的波阻抗，钢破片冲击铝壳体的起爆阈值最小。

(3)受到冲击的推进剂能否起爆和初始点火热点的数量有关，初始点火热点越多，推进剂越容易起爆，破片与发动机接触面积越大，产生的初始点火热点越多。球形破片与发动机壳体的接触面积远小于圆柱破片和立方体破片，球形破片的起爆阈值远高于圆柱破片和立方体破片，而圆柱破片和立方体破片接触面积相同。因此，它们的起爆阈值也相近。长宽比的增加，使得冲击接触面积减小，起爆阈值也随之增加。