动滑轮系统对延伸喷管展开动力学的影响①
2018-11-26任全彬尤军峰
陈 鹏,任全彬,尤军峰
(中国航天科技集团公司四院四十一所,西安 710025)
0 引言
在延伸喷管的结构中,作动筒是提供展开动力的重要机构,其动力学特性决定了喷管整体的展开过程。而双级延伸喷管中的作动筒不仅要提供动力,同时对喷管的展开起重要的限制和导向作用,保证了双级延伸锥到位的平稳与同步性。
在展开的整体系统中,作动筒中的动滑轮结构属于冗余结构,加入前后系统的自由度并不产生变化,但动滑轮的预紧力会通过影响作动筒内部以及与筒身连接处转动副的摩擦力,来对系统的动力学特性产生不可忽视的影响。由于布置在作动筒的内部,动滑轮系统不易加工装配,在运输与装配过程中,也可能产生扭转和脱开,对系统展开产生影响。为提高系统的可靠性,进一步了解动滑轮系统特性与展开特性之间的关系,对动滑轮系统进行动力学分析是十分必要的。
由于套筒式延伸喷管机构较为复杂,现有的理论研究大多是采用简化的整体系统,无法解决实际结构上遇到的具体问题。王成轩等[1]对作动筒的受力情况进行了简化,采用质心运动的分析方式对双级延伸喷管进行了动力学分析,但其中一、二级作动筒简化为质点,且对系统转动副摩擦力及展开到位的摩擦与碰撞未加考虑;阎德元等[2]基于达朗贝尔原理,对作动筒支座处的支反力进行了求解,但未考虑作动筒整体动力学特性,求解也较为保守;尤军峰等[3]通过对系统拉格朗日动力学方程的求解,分析了在燃气发生器作用下延伸喷管的展开特性,考虑到了实际系统中的各种阻力因素与展开到位的情况,计算得出了系统的展开动力学参数,但由于分析中将阻力简化为轴向的等效阻力,对阻力的产生没有具体考量,不利于系统的进一步优化分析;董飞等[4]在ADAMS中对延伸喷管进行了动力学仿真,对整体的动力学特性有较好的仿真重现,但其中对于阻力的定义同样是基于轴向等效阻力。
在文献中尚未有关于动滑轮系统对喷管展开动力学影响的分析,对动力学特性的仿真计算工作也较为少见。一方面,由于延伸喷管系统较为复杂,设计思路较多,为进行更加细节的分析,在仿真时需要调节大量参数,并根据实验数据进行校核,已有的仿真对展开力与摩擦力均采取了一定程度上的近似;另一方面,在实验中发现了喷管展开特性与动滑轮预紧力之间有一定的关系,需要进行进一步探究。
本文通过对简化模型的理论计算[5-7],以及在模型中基于实验进行的参数调节与仿真[8-11],分析了动滑轮预紧力对延伸喷管系统动力学特性的影响,将理论与仿真相结合,为动滑轮系统与延伸喷管整体的优化设计提供参考。
1 理论计算
1.1 方法与模型
由于在延伸喷管的周围,4个锁紧转折片和作动筒均匀间隔分布,径向力为对称分布的内力,作用在延伸锥体上,故计算模型中可对1/4模型轴向力进行考虑。因为主要研究对象是作动筒,将锁紧转折片的阻力简化为作用在作动筒上的轴向力,对作动筒进行力学分析。
简化前后的模型见图1。模型中,m0、m1、m2、m3分别是基础部分(包括内筒和基础喷管)、二级延伸锥部分(包括中筒和二级延伸锥)、一级延伸锥部分(包括外筒和一级延伸锥)和作动筒(包括内筒、中筒和外筒)的质量,简化模型中,平动参数通过各部分所受的轴向合力计算,而转动参数由作动筒整体受外力计算。
对模型的受力分析见图2。图2中,F为展开主动力,作用在外筒上,与端面保持垂直;F0、F02是滑轮力,根据动滑轮理论,F02的大小是两倍的F0;F1是中筒对外筒的正压力,F2是内筒对中筒的正压力;f1、f2是作动筒内摩擦力;fz1、fz2是等效轴向摩擦力,包括密封圈与转折片的影响;Fk1、Fk2是内力提供的径向力;FT1、FT2、FT3是连接作动筒与延伸锥的支座力,由于径向没有加速度,FT1、FT2的y向分量与Fk1、Fk2分别相等,x向分量的反作用力为延伸锥提供轴向加速度,且三者在y向上合力为0,在x向上的合力为作动筒提供加速度;L1是作动筒长度,随着展开过程变化,l0是二级支座上方的作动筒长度。

(a)延伸锥模型
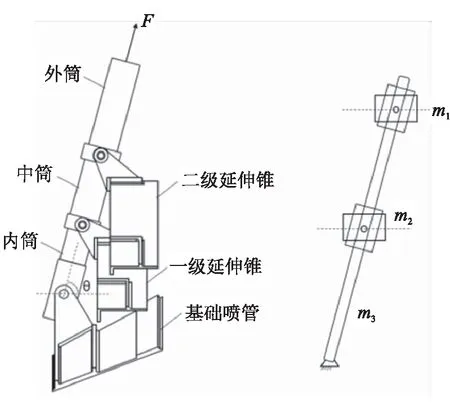
(b)简化后计算模型

图2 简化模型的受力分析
列式有
(1)
式中Tf为转动副的摩擦力矩;rf1、rf2、rf3为摩擦圆半径;T1、T2是外筒和中筒的预紧力,影响空载时的摩擦力;m4、m5分别是二级延伸锥和一级延伸锥的质量;2ωv1r为转动产生的科氏加速度。需要注意的是在运动的过程中,滑轮力的变化可能带来F1方向的变化。
由式(1)中第一个分式可知,当
Fcosθ-f1cosθ-F0cosθ-fz1-m1a1<0
(2)
时,F1反向,此时令
(3)
其他条件相同。
1.2 简化与求解
为讨论动滑轮预紧力F0对加速度的影响,需要在加速度的表达式中找出F0前的系数,进一步分析二者的关系。使转动副摩擦力矩Tf,作动筒额外长度l0为0,忽略科氏加速度,则有
对式(1)求解,得
(4)
其中
(5)
作动筒展开时的工作角度为25.74°<θ<75.03°。设μ1=μ2=0.2,易知当sinθ-μ1cosθ>0,cosθ-μ2sinθ>0,sin2θ+μ1cos2θ+μ2cos2θ-μ1μ2sin2θ>0,即11.31°<θ<78.69°时,m1、m2、m3、m4、m5前系数均为正值,包含了一般的工作状态,此时滑轮预紧力F0对加速度a1的影响由系数L5的正负值决定。
1.3 结果分析
在不考虑转动副摩擦Tf、作动筒额外长度l0以及科氏加速度的影响时,当滑轮预紧力小于临界值,L5=0,预紧力对展开没有影响;当滑轮预紧力大于临界值,L5<0,预紧力对展开起阻碍作用。
图3展示了基于理论模型,在不同预紧力下,延伸锥展开到位前的位移情况。由仿真结果可知,在预紧力较小时,预紧力对展开的影响不大;而在其较大时,随着预紧力的增加,展开的平均速度迅速降低。其变化趋势与简化后的理论计算结果基本一致。

图3 理论模型0.28 s展开位移
2 仿真结果与讨论
2.1 动力学特性仿真计算
由于理论计算的简化因素较多,难以进行定量分析,故对参数的具体讨论主要基于多体动力学软件的仿真计算。在ADAMS中对1/8喷管的实际模型进行动力学仿真,模拟在不同滑轮预紧力条件下,初始位置到展开到位前的动力学特性,并与实验所得展开位移曲线进行比较,结果见图4。

图4 延伸锥展开位移的实验与仿真数据对比
图4对仿真获得的位移曲线与实验曲线进行了比较。由图4可见,在忽略相位误差的情况下,实验获得的展开位移曲线与仿真有较好的一致性。在展开初期,实验曲线的加速度更大,中期的走向基本一致,而在展开末段,实验曲线与计算曲线基本重合。
仿真中假设模型受力情况完全对称,并采用1/8模型进行计算,但在实验中会产生振动与不对称的附加力;另外,实验中作动筒内压的加载与仿真中的主动力曲线有一定的差别。这些可能是误差产生的原因。
图5~图7中,展示了在不同预紧力下,第二级延伸锥的轴向位移、速度和加速度。0 N表示滑轮预紧力F0为0时的位移,40 N为滑轮预紧力40 N 时,以此类推。可看出,在不同的动滑轮预紧力下,作动筒均能在0.4 s内展开至平衡位置,展开曲线总体上保持了一致性,变化范围不大。随着预紧力增大,展开曲线总体呈现先加快后减慢的过程:在预紧力为40 N时,展开的平均速度要大于预紧力为0的情况;当预紧力达到150 N,展开的平均速度则要小于预紧力为0时。
在展开的不同阶段,速度和加速度变化并不保持一致。在展开初期,随着预紧力增大,加速度先增大后减小;但在展开末段,加速度随着预紧力的增大而增大。另外,速度与加速度的最大值均表现出增大趋势。
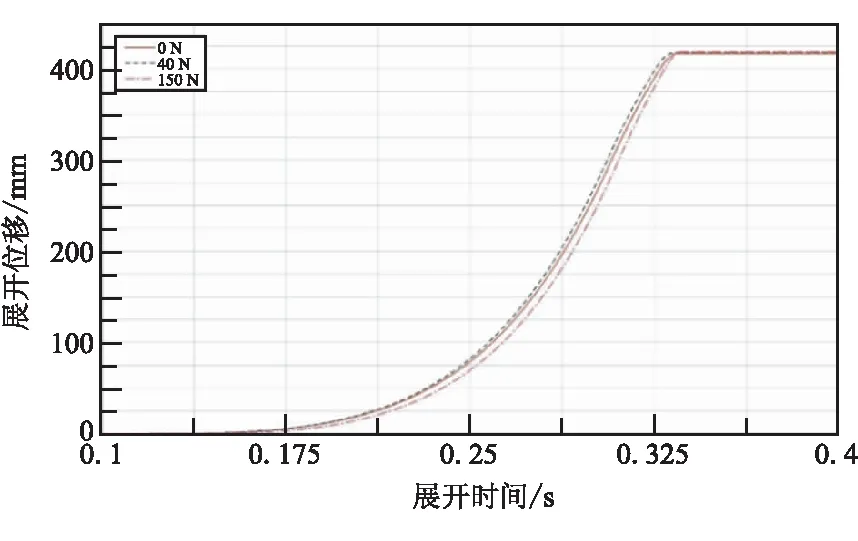
图5 不同预紧力下延伸锥展开位移
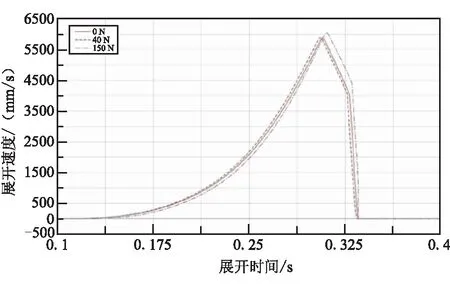
图6 不同预紧力下延伸锥展开速度
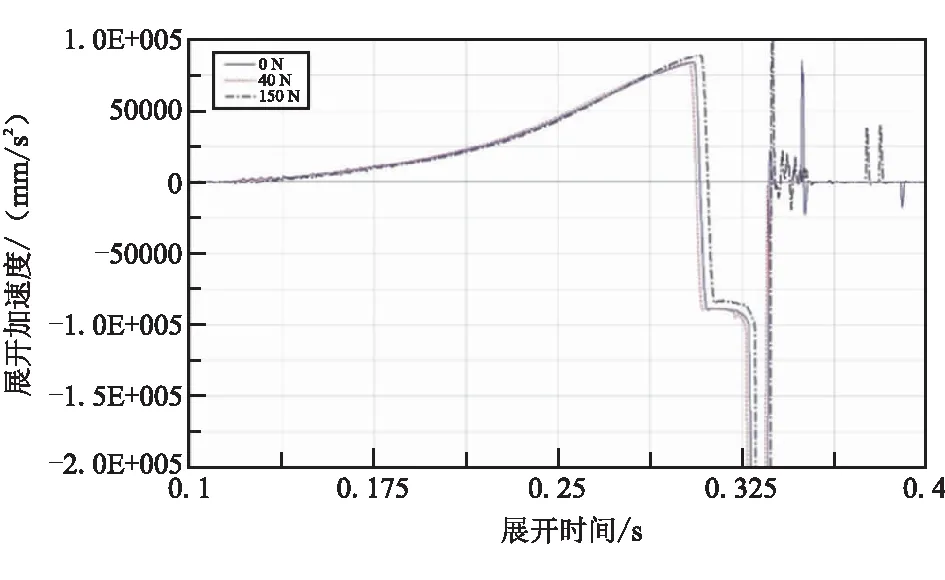
图7 不同预紧力下延伸锥展开加速度
图8给出了在展开即将到位(0.32 s)时,预紧力的变化对二级延伸锥展开位置的影响。从图8可看出,在展开到位之前,随着预紧力增大,延伸锥的展开位置呈现先增大后减小的趋势,即延伸锥展开的平均速度先增大后减小,且在预紧力约40 N时达到最大。这说明预紧力的适当增大,对延伸锥的展开起促进作用,但过大的预紧力会使展开的平均速度降低。
2.2 锁紧机构到位情况
实验中发现,动滑轮预紧力的大小与锁紧机构最终的到位情况有密切的联系。在动滑轮上的力过小甚至脱开的情况下,延伸喷管的展开无法到位,转折片无法完全锁紧。

图8 0.32 s时二级延伸锥位移情况
图9中展示了展开到位的不同情况。若转折片停在弹簧锁片上,锁紧机构无法完全到位,在工作压力与振动的作用下,延伸锥可能会产生回弹,造成延伸喷管的失效,对发动机的工作造成严重的影响,必须要避免这种情况的发生。

图9 展开到位的不同情况
在预紧力为0时,观察展开至平衡状态的模型,转折片停留在弹簧锁片上,在轴向拉力作用下,延伸锥容易产生回弹,锁紧机构工作失败。图10展示了在不同预紧力下的展开位移的变化。由计算结果看出,考虑到计算误差,随着预紧力的增大,延伸锥的展开位移也逐渐增大,在滑轮预紧力达到约65 N之后,展开位移达到最大值并保持稳定。观察此时的展开状态,发现锁紧机构完全到位,轴向拉力无法将延伸锥拉回,锁紧机构工作正常。因此,为避免发生回弹事故,动滑轮预紧力需大于65 N。
2.3 动滑轮的脱开
实验中发现,展开后的预紧力要比展开前的预紧力更小,这可能是由制造与装配误差导致的动滑轮系统脱开造成的。例如,理想状况下,若绳索半径1 mm,弹性模量E为1×105MPa,有效长度645.95 mm,预紧力15 N时,计算可知预紧力带来的绳索伸长量约为0.015 mm。因此,在运动过程中,预紧力会不断减小,直至中筒与外筒的相对位移差值大于0.015 mm之后,绳索会因为预紧力归零而脱开。

图10 展开到位位移的变化
图11所示为模型中一二级作动筒的相对位移差值。当位移差值大于预紧力带来的预拉伸量后,滑轮力归零,动滑轮脱开;预紧力足够大,使预拉伸量大于位移差值时,动滑轮可始终保持受力状态。图12给出了在理想状态下动滑轮系统最终的受力情况。由曲线可知,在初始预紧力达到62 N以上时,滑轮系统可避免脱开。
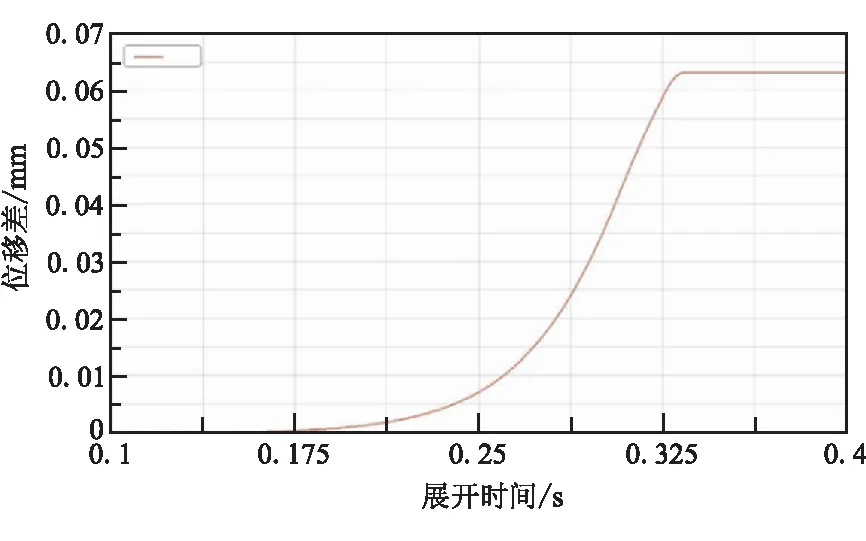
图11 一、二级作动筒之间的相对位移差

图12 初始预紧力与脱开情况
制造与装配误差同时也可能导致滑轮系统越拉越紧。若一二级作动筒之间的位移差值为负,则会导致展开后的预紧力比展开前的更大。
3 结论
(1)数值仿真得到的位移曲线与实验数据有较好的一致性,仿真模型可再现实验中的到位情况,可靠性较好。
(2)随着动滑轮预紧力的增大,展开到位前平均速度呈现先增大后减小的趋势,在40 N附近达到极大值,在约105 N时,达到与0 N时相同的水平,随后迅速降低。
(3)在预紧力较低时,锁紧机构无法在预定位置锁紧,可能会造成回弹事故,随着预紧力的增大,平衡状态下锁紧机构的逐渐到位,与实验观察的结果一致。当动滑轮预紧力大于65 N时,锁紧机构可完全到位。
(4)动滑轮系统会产生脱开的现象,造成预紧力的下降,以致动滑轮的失效。其原因可能是制造装配误差与动滑轮绳索的弹性拉伸。理想状况下,初始预紧力大于62 N时,可避免动滑轮系统的脱开。
(4)对动滑轮预紧力与展开动力学特性关系的研究,为优化延伸喷管的结构设计提供了理论参考,有助于进一步提高延伸喷管可靠性。
