拨开云雾见正解
2018-11-26张朝娣
张朝娣

了解数据的集中趋势和离散程度,可以更加有效地认识、利用数据.在学习本章时,同学们可能会出现以下一些错误,希望你们通过对以下题目的学习,能正确运用相关概念,分析数据的集中趋势和离散程度.
一、概念理解不清
例1 某商场为了了解产品A的销售情况,在上个月的销售记录中,随机抽取了5天A产品的销售记录,其售价x(元/件)与对应销量y(件)的全部数据如下表:
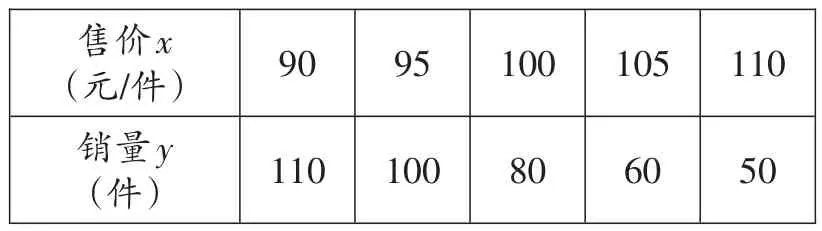
50售价x(元/件)销量y(件)90 95 100 105 110 110 100 80 60
则这5天中,A产品平均每件的售价为( ).
A.100元 B.95元
C.98元 D.97.5元
【错解】A或B.
错解原因:错误地认为A产品平均每件的售价与件数无关,是一个定值.本题中产品A的平均售价是由总销售额除以总销售量得到的.
【正解】

故选:C.
二、众数不是最大的数
例2 某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某一天每个工人的生产件数,获得数据如下表:

15 1生产件数(件)人数(人)10 1 11 5 12 4 13 3 14 2
则这一天16名工人生产件数的众数是( ).
A.5件 B.11件
C.12件 D.15件
【错解】D.
错解原因:把众数当成出现的最大的数据了.
【正解】众数是一组数据中出现次数最多的数据.
故选:B.
例3 10名工人某天生产同一零件,生产的件数分别是:15,17,14,10,15,19,17,16,14,12,则这一组数据的众数是________.
【错解】15.
错解原因:一组数据中出现次数最多的数据就是这组数据的众数,根据众数的意义,一组数据有时可以有不止一个众数,也可以没有众数.如2,3,4,7,9,这组数据中没有众数.
【正解】14,15,17这3个数各出现两次,且两次为最多次数,所以这组数据的众数为14,15,17.
三、审题不清
例4 一组数据2,4,6,4,8的中位数为( ).
A.2 B.4 C.6 D.8
【错解】C.
错解原因:没有对数据排序.将一组数据按照从大到小(或从小到大)顺序排列好,当这组数据的个数为奇数时,中位数就是中间那个数据,当这组数据的个数为偶数时,中间两个数据的平均数就是这组数据的中位数.
【正解】对数据排序:2,4,4,6,8(或8,6,4,4,2),中间数据为4.
故选:B.
例5“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中3个年级推选出来的15名领操员进行比赛,成绩如下表:_______________________

_______________________________________10________________________________________4成绩/分______人数/人______7______2_____8______5_____9__________4_________
中位数是________.
【错解】8.5或4.5.
错解原因:将成绩7,8,9,10排序,8和9的平均数是8.5;将人数2,5,4,4排序,5和4的平均数是4.5.对于这种求表格中数据中位数的题目,首先要看清楚研究对象,此处要求成绩的中位数,则确定要分析的是以成绩为对象的那组数据.
【正解】若从小到大排列成绩,则为2个7,5个8,4个9,4个10,则中位数为第八个数,中位数为9.
四、求最值时没有分类讨论
例6 已知一组数据:-2,1,5,x的极差为11,则x的值为________.
【错解】9.
错解原因:一组数据中最大值与最小值的差叫做这组数据的极差.即极差=最大值-最小值.本题中错解错误地认为-2是最小值,x是最大值,这样,求出x为9,忽视了当x为最小值时的情况.
【正解】因为5-(-2)=7<11,所以x可能是最大值,也可能是最小值.x-(-2)=11,x的值为9;5-x=11,x的值为-6.所以x的值为9或-6.
五、记错公式或概念
例7 甲、乙两名同学的5次射击训练成绩(单位:环)如下表._____________________

__________________甲__________________乙7____6____8____10____9____9_____8____7_____8__8__
比较甲、乙这5次射击成绩的方差s甲2,s乙2,结果为:s甲2____________s乙2.(选填“>”“=”或“<”)
【错解】“=”或“>”.
错解原因:方差是反映一组数据波动大小的一个量,通常用s2表示.计算时,经常要用到公式:

记错公式及计算能力不过关是造成错误的主要原因.
【正解】x甲=8,x乙=8,所以s甲2==2.
故填:“<”.
例8 已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是( ).
A.3,2 B.3,4
C.5,2 D.5,4
【错解】D.
错解原因:认为数据的平均数不变,方差不变,记错结论.
【正解】由平均数的定义可得,a+b+c=15.
那么数据a-2,b-2,c-2的平均数为:

数据a-2,b-2,c-2的方差为:

故选:B.
六、综合应用
例9 某商场甲、乙、丙3名业务员5个月的销售额(单位:万元)如下表:

销售人员月份甲乙第一月第二月第三月第四月第五月7.2 9.6 9.6 7.8 9.3 5.8 9.7 9.8 5.8 9.9丙 4 6.2 8.5 9.9 9.9

(1)根据上表中的数据,将下表补充完整:

销售人员统计量甲乙丙8.2平均数(万元)中位数(万元)众数(万元)9.3 9.6 7.7 8.5 5.8
(2)甲、乙、丙3名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.
【错解】(2)赞成甲、乙、丙3名业务员中的一位,但同时否定另两位.
错解原因:审题不清,应用统计量概念不合理.
【正解】(1)x甲=8.7.
将乙组数据从小到大排列为:5.8,5.8,9.7,9.8,9.9,其中处于最中间的数为9.7,所以乙的中位数为9.7.
因为丙组数据中出现次数最多的数据是9.9,所以丙组数据的众数为9.9.
(2)若从平均数的角度分析,甲的平均数最大,所以甲的销售业绩最好.
若从中位数的角度分析,乙的中位数最大,所以乙的销售业绩最好.
若从众数的角度分析,丙的众数最大,所以丙的销售业绩最好.
同学们,每个人都不可避免犯错,错误伴随着我们学习、成长,只要我们善于总结错误的原因,那么我们会更接近成功.让我们灵活运用所学,让错误助力成功,加油哦!
