学会思考掌握方法

邵 娟

学会思考，对同学们来说，是一生中最有价值的本钱.近几年“数据的集中趋势和离散程度”在中考中出现的频率越来越高，相信同学们通过以下的学习，能对初中数学中“数据的集中趋势和离散程度”的解题策略方法有所了解与掌握.

一、熟知概念，直击要害

例1 据统计，某住宅楼30户居民5月份最后一周每天实行垃圾分类的户数依次是：27，30，29，25，26，28，29，那么这组数据的中位数和众数分别是（ ）.

A.25和30 B.25和29

C.28和30 D.28和29

【解析】从小到大排列此数据为：25，26，27，28，29，29，30.数据29出现了两次，所以29为众数；中间的数是28，所以28是中位数.

故选：D.

例2 一组数据2，1，2，5，3，2的众数是（ ）.

A.1 B.2 C.3 D.5

【解析】在数据2，1，2，5，3，2中，2出现3次，出现次数最多，所以众数为2.

故选：B.

【点评】例1、例2属于基础题，考查了同学们确定一组数据的中位数和众数的能力.部分同学往往对这个概念理解不清楚，求解方法不明确.大家注意，找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个数来确定中位数.如果数据是奇数个，则正中间的数即为中位数；如果数据是偶数个，则找中间位置两个数的平均数.注意众数可以有不止一个.

例3 体育课上，某班两名同学分别进行了5次短跑训练，要判断哪一名同学的成绩比较稳定，通常需要比较两名同学成绩的（ ）.

A.平均数 B.方差

C.频数分布 D.中位数

【解析】方差反映一组数据波动大小，是反映这组数据稳定程度的量.方差越大，表明这组数据偏离平均数的程度越大，即波动越大，反之也成立.故要判断哪一名同学的成绩比较稳定，通常需要比较这两名同学5次短跑训练成绩的方差.故选：B.

二、熟记公式，直接套用

例4 某排球队6名场上队员的身高（单位：cm）是：180，184，188，190，192，194.现用一名身高为186cm的队员换下场上身高为192cm的队员，与换人前相比，场上队员的身高（ ）.

A.平均数变小，方差变小

B.平均数变小，方差变大

C.平均数变大，方差变小

D.平均数变大，方差变大

【解析】方法一（计算）.

原数据的平均数为：

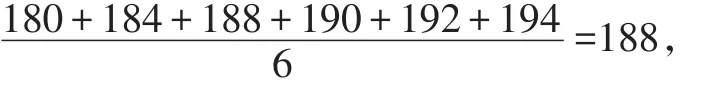
原数据的方差为：

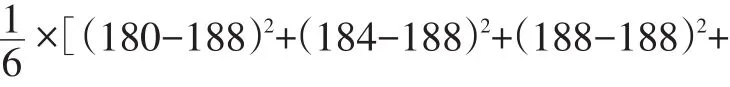
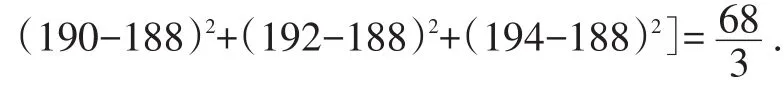
新数据的平均数为：

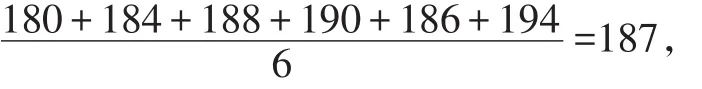
新数据的方差为：

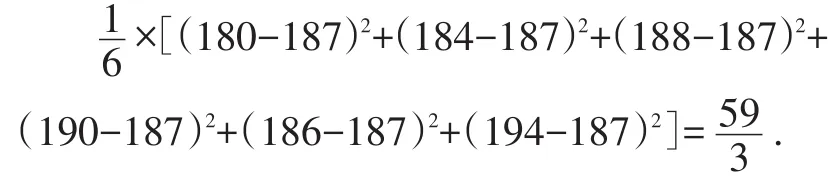
所以平均数变小，方差变小.

方法二（观察）：从题意可知，192＞186，所以平均数一定变小.同时，这组数据呈上升趋势，将192换成186，上升趋势变缓，方差变小.

故选：A.

例5 为了帮助市内一名患“白血病”的中学生，东营市某学校数学社团15名同学积极捐款，捐款情况如下表所示，下列说法正确的是（ ）.

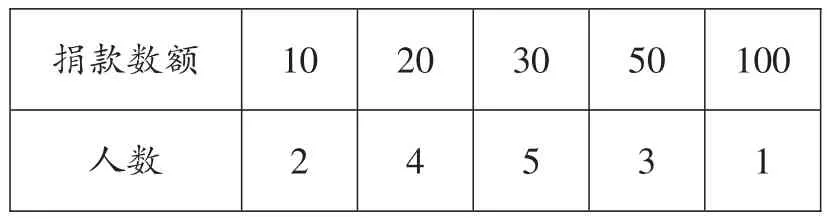
捐款数额10 20 30 50 100人数2 4 5 3 1

A.众数是100 B.中位数是30

C.极差是20 D.平均数是30

【解析】该组数据中出现次数最多的数是30，故众数是30，不是100，所以选项A不正确.

该组共有15个数据，其中第八个数据是30，故中位数是30，所以选项B正确.

该组数据的极差是100-10=90，故极差是90，不是20，所以选项C不正确.

该组数据的平均数是：

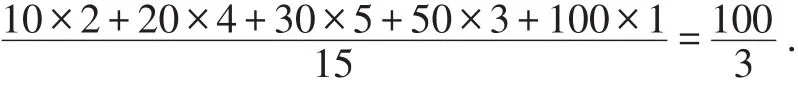
平均数不是30，所以选项D不正确.

故选：B.

【点评】这两题属于中档题，考查同学们对平均数、极差、方差公式的运用，所以在平常的学习中，同学们一定要熟记本章节的公式，做到“公式不离手，概念不离口”.

三、分析数据，巧用结论

例6 甲、乙、丙、丁4支仪仗队队员身高的平均数及方差如下表所示：

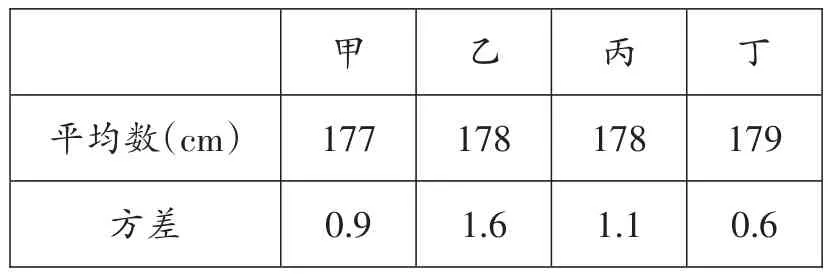
乙甲丙丁179 0.6平均数（cm）方差177 0.9 178 1.6 178 1.1

哪支仪仗队队员的身高更为整齐？

A.甲 B.乙 C.丙 D.丁

【解析】因为甲、乙、丙、丁4支仪仗队队员身高的方差中丁的方差最小，所以丁仪仗队队员的身高更为整齐.

故选：D.

例7 如果一组数据6，7，x，9，5的平均数是2x，那么这组数据的方差为（ ）.

A.4 B.3 C.2 D.1

【解析】根据题意，得：

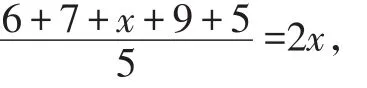
解得：x=3.

则这组数据为6，7，3，9，5，其平均数是6，所以这组数据的方差为：×［（6-6）2+（7-6）2+（3-6）2+（9-6）2+（5-6）2］=4.

故选：A.

【点评】方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数的程度越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数的程度越小，即波动越小，数据越稳定.

四、生活数学，数学生活

例8 超市销售人员在一段时间内销售了同一品牌不同尺码的鞋子，它们的销售量如下表：

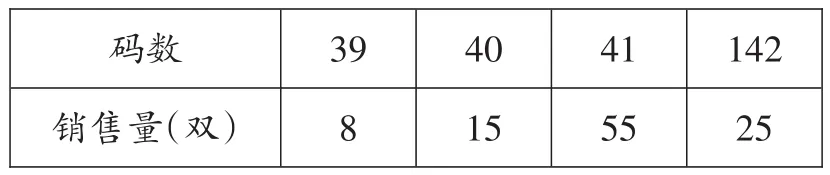
142 25码数销售量（双）39 8 40 15 41 55

建议超市将（ ）的鞋子进货多一些.

A.39码 B.40码 C.41码 D.42码

【解析】在4个码数的销售量中，41码的鞋子销售量最多.

故选：C.

例9 11名同学参加数学竞赛初赛，他们的得分互不相同，按从高分到低分进入复赛的原则，取前6名同学参加复赛.现在小明已经知道自己的分数，如果他想知道自己能否进入复赛，那么还需知道所有参赛学生成绩的（ ）.

A.平均数 B.中位数

C.众数 D.方差

【解析】11人成绩的中位数是第六名的成绩.参赛选手要想知道自己是否能进入前6名，只需要了解自己的成绩以及全部成绩的中位数，比较即可.由于总共有11个人，且他们的分数互不相同，第六名的成绩是中位数，要判断自己是否进入前6名，故应知道中位数.

故选：B.

【点评】数学来源于生活，而又服务于生活.本题考查了我们实际生活的问题，把实际问题数学化.例8中41码的鞋子的销售量比较多，超市肯定将销售量最多的进货多一些，考查了同学们的生活经验.

其实这一章节的内容在中考中对于大多数同学来说是送分题，它主要考查的是基本的概念和公式.希望同学们在学习中理清概念，熟记公式，那么考试时所有的问题都能轻松应对.

小试牛刀

1.某小区20户家庭的日用电量（单位：千瓦时）统计如下：

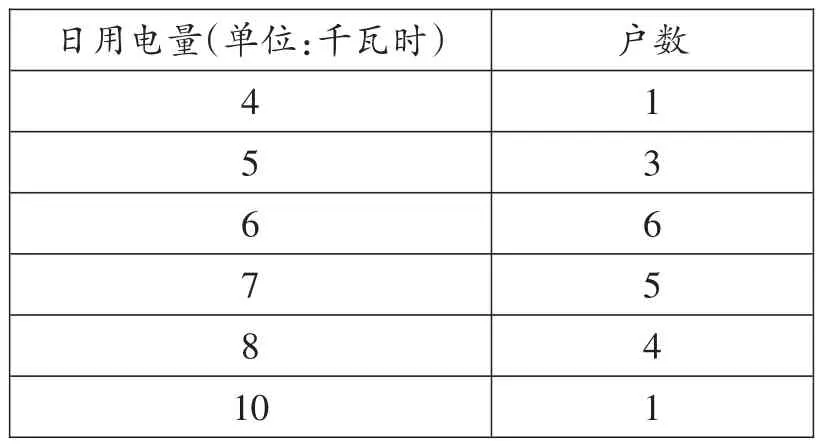
日用电量（单位：千瓦时）户数4 5 6 7 8 1 0 1 3 6 5 4 1

这20户家庭日用电量的众数、中位数分别是（ ）.

A.6，6.5 B.6，7

C.6，7.5 D.7，7.5

2.九年级一班和二班每班选8名同学进行投篮比赛，每名同学投篮10次，对每名同学投中的次数进行统计.甲说：“一班同学投中次数为6个的最多.”乙说：“二班同学投中次数最多的与最少的相差6个.”上面两名同学的议论能反映出的统计量是（ ）.

A.平均数和众数 B.众数和极差

C.众数和方差 D.中位数和极差

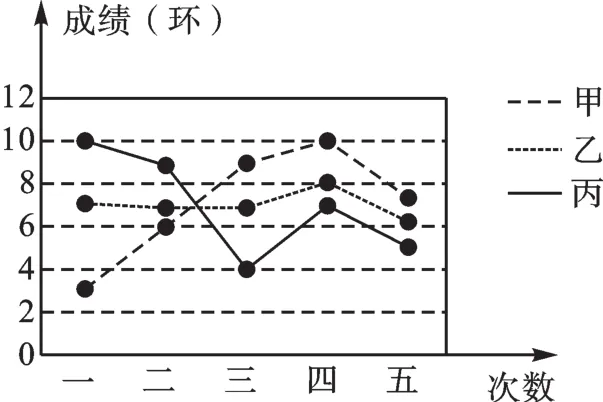
3.甲、乙、丙3人进行飞镖比赛，已知他们每人投5次的成绩如图，那么3人中成绩最稳定的是 .

4.学校商店在一段时间内销售了4种饮料共100瓶，各种饮料的销售量如下表：

品牌销售量（瓶）甲乙丙丁12 32 13 43

建议学校商店将（ ）品牌的饮料进货多一些.

A.甲 B.乙 C.丙 D.丁

扫二维码关注公众号，输入“2018年11月数学”查答案。