“数据的集中趋势和离散程度”难点解析

李兆龙

难点一 求众数和中位数

例1 某校对部分参加夏令营的中学生的年龄（单位：岁）进行统计，结果如下表：

人数月收入／元45000 18000 10000 5500 4800 3400 3000 2000 1 1 1 3 6 1 1 1 1

17 1年龄人数13 1 14 2 15 2 16 3

则这些学生年龄的众数和中位数分别是（ ）.

A.16，15 B.16，14

C.15，15 D.14，15

【解析】根据图表数据，可知16岁的人数最多，共3人，所以众数是16岁；这9名学生的年龄从小到大排列后，第五名学生的年龄是15岁，所以中位数是15岁.故选：A.

【点评】一组数据中出现次数最多的数据就是这组数据的众数.找中位数时，必须先把数据按照从小到大（或从大到小）的顺序排序.如果数据的个数是奇数，则中间那个数据就是这组数据的中位数；如果数据是偶数个，则中间那两个数据的算术平均数就是这组数据的中位数.中位数和众数不同，众数指出现次数最多的数，一组数据有时可以有不止一个众数，也可以没有众数，而中位数只能有一个.

难点二 “三数”的应用

例2 某公司共有25名员工，下表是他们月收入的资料.

（1）该公司员工月收入的中位数是______元，众数是_____元.

（2）根据上表，可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由.

【解析】（1）根据题意，可知员工月收入的中位数是3400元，众数是3000元.

（2）答案不唯一，用中位数和众数来描述更为恰当.如选择中位数理由如下：这组数据中有差异较大的数据，这会导致平均数较大.该公司只有3人的月收入达到了6276元，用平均数来反映全体员工的月收入水平不合适.该公司员工月收入的中位数为3400元，除去月收入为3400元的员工，一半员工收入高于3400元，一半员工收入低于3400元.因此，利用中位数可以更好地反映这组数据的集中趋势.

【点评】平均数反映一组数据的“平均水平”，与每一个数据都有关，易受极端值的影响；众数反映一组数据的“多数水平”，其大小只与部分数据有关，有时不唯一，有时也没有；中位数反映一组数据的“中等水平”，当一组数据的个别数据偏大或偏小时，用中位数来描述该组数据的集中趋势就比较合适.

难点三 方差

例3 小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示.通常新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是 .

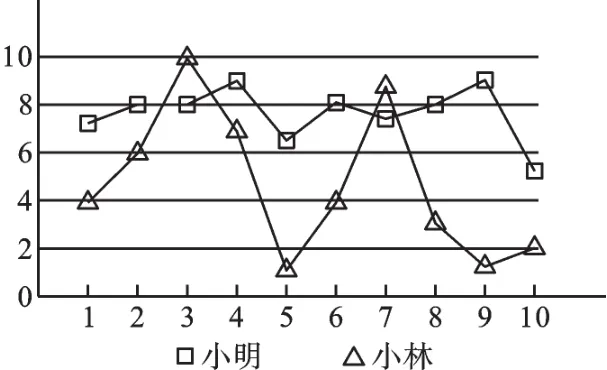
【解析】我们通过观察图像，可以看出，小明的成绩比较集中，波动较小，即方差比较小，而小林成绩波动较大.根据方差的意义，可以知道，波动越大，成绩越不稳定.又已知通常新手的成绩不太稳定，故新手是小林.

【点评】本题考查方差的意义.各数据与数据平均数的差的平方和的平均数叫做方差，反映这组数据偏离平均数的程度.方差越大，这组数据偏离平均数的程度（离散程度）就越大，即波动就越大，数据越不稳定；方差越小，表明这组数据的离散程度越小，分布越集中，各数据偏离平均数的程度就越小，波动也越小，数据越稳定.本题没有给出小林和小明射击成绩的具体数据，只给出了数据图像，不能利用方差的计算公式计算出方差值.因此，我们要另辟蹊径，想到利用方差的意义对图像进行分析.

难点四 “三数与两差”的综合应用

例4 为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动.学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射10发子弹，成绩用如图的折线统计图表示（甲为实线，乙为虚线）：

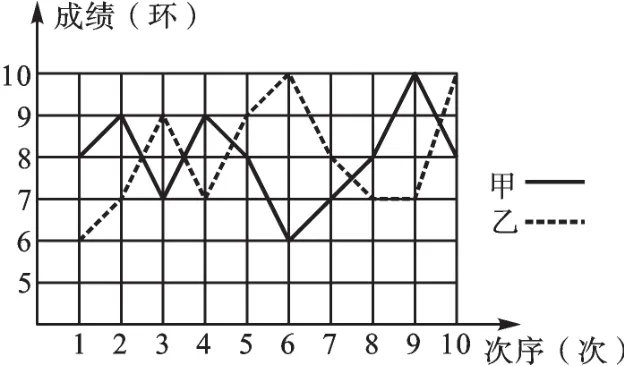
（1）依据折线统计图，得到下面的表格：

射击次序（次）甲的成绩（环）乙的成绩（环）1 2 3 4 5 6 7 8 9 1 0 8 9 7 9 8 6 7 a 1 6 7 9 7 9 1 0 8 0 8 7 b 1 0

其中a=_______，b=_______.

（2）甲成绩的众数是_______环，乙成绩的中位数是_______环.

（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？

【解析】（1）由折线统计图知a=8，b=7.

（2）甲射击成绩出现次数最多的是8环.把乙成绩按从小到大顺序排列，中间两个数的算术平均数是7.5，所以乙成绩的中位数是7.5环.

（3）因为x甲=x乙=8（环），s甲2=1.2，s乙2=1.8，s甲2＜s乙2，故甲成绩更稳定.

【点评】大家平时应注意结合一些具体事例去理解这部分知识，要逐步体会这些知识在实际生活中的应用，而不是关注一些具体计算.

相信以上学习能够帮助同学们巩固本章相关知识，化难为易，真正适应中考命题.