Reliable and Load Balance-Aware Multi-Controller Deployment in SDN

Tao Hu, Peng Yi＊, Jianhui Zhang, Julong Lan

National Digital Switching System Engineering & Technological R&D Center, Zhengzhou 450002, China

Abstract: Software Defined Networking(SDN) provides flexible network management by decoupling control plane and data plane.However, such separation introduces the issues regarding the reliability of the control plane and controller load imbalance in the distributed SDN network, which will cause the low network stability and the poor controller performance. This paper proposes Reliable and Load balance-aware Multi-controller Deployment (RLMD) strategy to address the above problems. Firstly, we establish a multiple-controller network model and define the relevant parameters for RLMD. Then, we design the corresponding algorithms to implement this strategy. By weighing node efficiency and path quality, Controller Placement Selection (CPS)algorithm is introduced to explore the reliable deployments of the controllers. On this basis,we design Multiple Domain Partition (MDP)algorithm to allocate switches for controllers according to node attractability and controller load balancing rate, which could realize the reasonable domain planning. Finally, the simulations show that, compared with the typical strategies, RLMD has the better performance in improving the reliability of the control plane and balancing the distribution of the controller loads.

Keywords: software defined networking;controller; reliability; load balancing; network optimization

I. INTRODUCTION

As a new network architecture, Software Defined Networking (SDN) has achieved the full decoupling between control plane and data plane, and brings abstractions to the control layer of the network by providing open interfaces [1]. Generally, SDN has the remarkable characteristics of centralized control and programmable network, and the research about controllers and switches [2-3] has attracted broad attentions in the last decade.

With the expansion of the network scale,the single centralized controller couldn’t meet the requirement of the existing traffic [4-5].Therefore, the logically centralized but physically distributed multi-controller architecture has been proposed to improve the scalability of controller and avoid the single point of failure [6], such as HyperFlow [7], Onix [8], Kandoo [9] and so on. The switches are allocated for different controllers to construct several SDN domains. Meanwhile, controllers in each domain interact with each other and complete the processing of the flow requests together.

In this paper, RLMD strategy is proposed to improve the reliability of the control plane and balance controller loads for the distributed SDN network.

Although the introduction of the distributed multi-controller architecture enhances the flexibility and elasticity of the network, it brings some great challenges for multi-controller deployment. In the real network topology, nodes and links can’t always hold on the normal running state [10]. Both the physical damage and transmission congestion will cause link interruption and node isolation [11]. In addition, due to the requests of the switches are the main parts of controller loads, the unbalanced distribution of switches will bring about the big loads difference between controllers [12].In particular, this paper focuses on the scenario that traffic status in the network is known and shows low fluctuation.

In recent years, the research about controller deployment could be summarized as two aspects. In the first category [13-22], it considers several network parameters (e.g. delay,traffic and hop) and implements multi-objective hybrid optimization to deploy controllers.Such studies could improve the communication quality and reduce the response delay.However, they ignore the impact of connectivity and lack the path protection mechanism.Once the controllers are overloaded or control links break down, they will lead to communication interruption and cross-domain interaction. In the second category [7-9, 23-27],it pays attention to the reliability indexes and completes the controller deployment according to the reliabilities of nodes and links. The weaknesses are short of considering controller loads, which may cause load imbalance and reduce network throughput.

To address the problems in above-mentioned researches, this paper proposes Reliable and Load balance-aware Multi-controller Deployment (RLMD) strategy. Differing from the previous studies that only focus on the reliability or the controller load balancing,we make the first attempt to design a progressive scheme for RLMD, which successively achieves the reliable deployments of controllers and the balanced distributions of controller loads. In summary, the main contributions are as follows.• We explore to build the multi-controller network model and define several relevant parameters (node efficiency, node attractability, path quality, controller load balancing rate and so on) for RLMD. Specifically,we implement this strategy as two progressive phases, and design the corresponding algorithms, which are Controller Placement Selection (CPS) and Multiple Domain Partition (MDP).

• For enhancing the reliability of the control plane, we introduce CPS algorithm. It evaluates the reliability of nodes in the network by adjusting the proportion of node efficiency and path quality with the weight parameter, and implements node iteration to select the appropriate controller locations.Moreover, CPS sets the balance factor to optimize the distributions of controllers in the network.

• In terms of achieving load balancing among controllers, we improve K-center clustering approach [13] and design MDP algorithm.Based on the controller locations selected by CPS, MDP allocates the switches for controllers to realize the reasonable network planning according to node attractability and controller load balancing rate.Meanwhile, the redundancy function is introduced to cope with the network traffic burst in MDP.

• The performance of RLMD is validated through comparing with typical strategies in experiments. The results show the nice property of RLMD in both improving the reliability of the control plane and balancing the controller loads.

The rest of this paper is organized as followings. Section II gives the related work.Section III describes the problem of multi-controller deployment, and formulates the RLMD model. The corresponding algorithms are designed for RLMD in Section IV. Section V provides the evaluation and analysis of simulations. Section VI concludes this paper.

II. RELATED WORK

Currently, the research work about multi-controller deployment can be divided into two categories.

In the first category, controllers are deployed according to different network parameters (delay, traffic, hop and so on). [13]defines a capacitated controller problem, and introduces K-center method, which takes into consideration the load of controllers and implements clustering to minimize the latencies between controllers and switches, to place controllers. [14] firstly proposes the problem of controller deployment, and focuses on the average delay and the maximum delay in the network. By building the corresponding mathematical model, it determines the optimum deployment states of controllers. In [15], it also integrates hop and delay, and dynamically explores the locations and quantity of controllers based on the network situation. [16] introduces a mathematical model for controller placement, which simultaneously determines the optimal numbers, locations, types of controllers and the interconnections between all the network elements. In [17], the authors design Fully Polynomial Time Approximation Schemes (FPTAS) to leverage the centralized controller to get significant improvements in network utilization as well as to reduce packet losses and delays. [18] designs ElastiCon with double overload threshold values to decide the shift of controller load. [19] introduces a load variance-based synchronization (LVS) method to improve the load balancing performance in multi-domain network. LVS conducts state synchronization among controllers if and only if the load of a specific server or subdomain exceeds a certain threshold. [20] designs the zero-sum game model between switches and controllers to implement elastic control. It then implements the decentralized mechanism of game-based decision. [21] develops a multi-controller deployment scheme based on delay optimization. A bee colony algorithm is used to minimize the setup time of the flow table and the synchronous delay overheads between controllers. [22] has addressed the dynamic Controller Placement Problem (CPP),which consists of determining the locations of controllers to bound communication latency and determining the number of controllers to support dynamic load.

In the second category, controllers are deployed according to the reliability of the network. Studies have proposed the flat and the vertical controller deployment architecture[7-9]. On this basis, [23] tries to maximize the reliability of SDN control plane. It introduces a new metric, called expected percentage of control path, to characterize the reliability.Meanwhile, Reliability-aware Controller (RC)is demonstrated as a NP-hard problem, and several placement algorithms are examined to solve this problem. [24] proposes Survivor, which mainly thinks about three aspects included path diversity, capacity and failover mechanisms. It correctly explores the path diversity and considers capacity-awareness proactively for controller deployment to avoid controller overload, especially during failover.[25] presents Dynamic Controller Assignment(DCA) to minimize the average response time of the control plane. DCA is formulated as a stable matching problem with transfers,and designs a two-phase algorithm which integrates key concepts from both matching theory and coalitional games. [26] implements an elastic mechanism to enhance network resiliency through controller placement and control-traffic routing. When the output interface breaks down, a protected switch starts the backup interface to reconnect the controller,which could achieve fast failover of the traffic.[27] introduces POCO, a framework for Pareto-based Optimal COntroller placement that provides operators with pareto optimal placements with respect to controller failure, isolated node, load balancing and inter-controller latency. The availability of POCO is analyzed in detail via an evaluation featuring numerous real world topologies.

III. PROBLEM AND FORMULATION

In this section, we will describe the problems of multi-controller deployment. Then, based on the evaluation indexes of the network, we set up the corresponding mathematical model for RLMD and define the relevant parameters.

3.1 Problem description

Generally, we consider the controller as a network component or a software-only application, and the communication mode is the in-band method. All network nodes have the right to install controllers, and thus the controller connects several switches to construct SDN domain. In order to simplify the analysis and reduce the controller installation cost, we assume that each controller node only deploys one controller to meet the processing requirements of all flows. Therefore, the problems of controllers in the distributed SDN network are how to realize the reliable deployment of controllers and how to allocate switches for controllers to plan SDN domains.

When we choose the controller deployment nodes, the selected nodes must have the low failure probability. What’s more, the controller is also more willing to deploy on the node with higher flow request rate. This is because when a node possesses both switch and controller at the same time, the delay and hops between the switch and the controller are negligible on the node. Meanwhile, on this specific node, the flow requests of the switch could be dealt preferentially by the controller without considering the distance constraint,and the control resources are fully utilized. In addition, due to controllers communicate with switches via the physical links, we also take into account the link states before selecting the controller nodes, such as short link distance between switch and controller, low link failure probability and high link bandwidth. After the controller locations are determined, we will allocate switches for each controller to construct the domains reasonably, which guarantee the balanced distributions of switches and controller loads in the network.

As shown in figure 1, there are 10 nodes in the network, and each node has the specific sequence number. Considering the states of all links are same in this network, we will select the reasonable nodes for deploying controllers. Definitely, the network is divided into two domains, and we use white color and gray color to represent domain 1 and domain 2,respectively. Meanwhile, OpenFlow switches are deployed on the circular nodes, and SDN controllers are deployed on the star nodes.In figure 1(a), the controllers are deployed on node 1 and node 9. Two domains contain three and five switches, respectively. When the link between node 1 and node 2 interrupts,node 1 becomes an isolated node, meanwhile,the controller in node 1 loses efficacy, which will severely damage the communication performance in the network. To meet the requirements of the control plane reliability and controller load balancing, we adjust the locations of controllers, and the results are displayed in figure 1(b). Because node 3 has the higher flow request rate compared with other nodes, the controller location is changed from node 1 to node 3. Moreover, we also alter the attribution of the switch on node 5 for domain reasons. After adjustment for the location of the controller and the planning of domains, the reliability of the control plane has been improved obviously, and the distribution of controller loads becomes more balanced in figure 1(b).

3.2 Model formulation

Using the above analysis as a foundation, we propose RLMD strategy. This strategy adopts the progressive design, which includes two stages. Firstly, it optimizes the controller location based on the characteristics of nodes and links to maximize the reliability of the control plane. Then, it determines the connection relationships between switches and controllers to construct the reasonable SDN domains to balance controller loads. Next, we set up the mathematical model for RLMD and define relevant parameters.

We model SDN as a graph G=(V,E),where V represents the set of nodes and E represents the set of links. We assume that the network has been divided into k domains. The specific network symbols are shown in Table I. ymnand πncmare binary variables. ymnis theconnection between adjacent nodes, where ymn=1 represents vmand vnare interconnected, otherwise ymn=0.is the location of the controller, where=1 represents mthcontroller is deployed on node vn, otherwise=0.

Table I. Summary of symbols for RLMD.

Fig. 1. The multi-controller deployment in SDN.

The closeness degree of nodes is represented as CD in Eq. (1), where n is the total number of nodes. The shorter distance of adjacent nodes, the higher CD.

The reliability degree of node viis represented as RDi, which is the average of the reciprocal summation of distance between viand the other nodes, as shown in Eq. (2). The higher RDi, the better connectivity of vi.

Theorem 1. CD is arithmetic mean of all RDiin the network.

Proof. The computation of CD is shown in Eq. (1), and we transform this equation. The result is displayed in Eq. (3).

For a given node vi, CD can be expressed in another way in Eq. (4).

Therefore, we can conclude that CD is the arithmetic mean of all RDiin Eq. (4), and the original proposition has been proved.

Definition 1. Node efficiency is a comprehensive assessment of node performance in the network. Node efficiency contains three parts that are the link quantity ratio, the reliability degree of node and the flow request rate of switch on the node, where the link quantity ratio indicates the proportion of the links connected to this node and all links. The efficiency of node viis set as NEiin Eq. (5).NE is the total node efficiency of all controller nodes in Eq. (6).

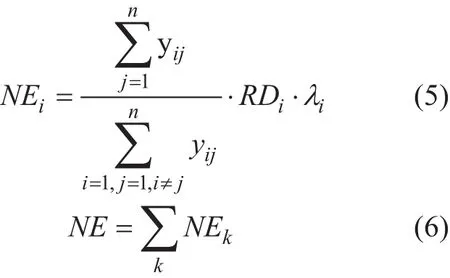
Definition 2. Node attractability. When the location of the controller is determined, we must determine the connection relationships between switches and controller. Therefore,we introduce the definition of node attractability. For controller cj, the attractability of node viis defined asin Eq. (7), where lijis the shortest distance between viand cj. If cjis deployed on node vi, then=∞. It easily concludes that the value ofis inversely proportional to the flow request rate and distance.

Link outage probability is represented as Poutage(eij). In this paper, link outage represents there are physical interruptions between adjacent nodes. As shown in Eq. (8), Poutage(eij) is related to the length of link, where punitis the failure probability of link per unit length.

Link congestion probability is represented as Pcongest(eij), which is related to the bandwidth and transmission traffic of the link eij.Pcongest(eij) is shown in Eq. (9), where σijis the direction factor of traffic. σij=1 represents that the direction of traffic is from source node vito destination node vj, otherwise σij=0.

Definition 3. Path quality. For a given network, we evaluate the link according to link distance dij, link bandwidth ωijand link failure probability Pfailure(eij), and Pfailure(eij) =Poutage(eij) +Pcongest(eij) .Therefore, we can summarize that Pfailure(eij) is also related to dijand ωij. Therefore, the path quality of eijis defined as PQij, shown in Eq. (10).

Equation (11) represents the sum of path qualities of links connected to node vi. Equation (12) shows that the sum of path qualities of links connected to all controllers. Equation(13) ensures that the links in the network are non-directional. Equation (14) presents that the node itself can’t form a loop.

Definition 4. Controller load balancing rate. When we compute the controller loads,the number of switches and flow request rates should be considered in the meantime. Therefore, by computing and summing the ratio of domain load to network load of all domains,we define the controller load balancing rate as CLBR in Eq. (15), where Γjis the number of switches in the jthdomain. Under the ideal state, the flow request rates of switches are the same, and the number of switches connected to each controller is equal. Therefore, the ideal value is CLBR*=1 k.

Based on the above definitions, we must consider node efficiency, path quality and controller load balancing rate simultaneously in the process of deploying controllers. Node efficiency and path quality promise the reliable selection of the controller location, and controller load balancing rate ensures the reasonable domain planning. The objective function of RLMD is Object in Eq. (16), which maximizes PQ, NE and CLBR through seeking the logical approach.

Equation (17) shows that k controllers have been able to manage the entire network.Equation (18) ensures the total flow requests processed by the single controller can’t exceed the processing capacity of the controller.Equation (19) represents there is no possible that all links break down in the meantime.

IV. ALGORITHM DESIGN

We design the corresponding algorithms to realize max[P Q,N E,C LBR] for RLMD. Due to the object function contains different tuning parameters, this paper adopts progressive processing method. For max[P Q,N E], Controller Placement Selection (CPS) algorithm is designed to explore the reliable deployments of controllers. On the basis of CPS, for max[CLBR], we improve the existing K-center and design Multiple Domain Partition (MDP)algorithm to achieve the reasonable SDN domain planning.

4.1 Controller placement selection(CPS)

When selecting controller locations, we must consider all nodes in the network. If one node is suitable for deploying controllers,it might be because this node has high node efficiency and the qualities of paths connected to this node are nice. Therefore, CPS considers NE and PQ in the meantime, and introduces the weight parameter α (0≤α≤1)to adjust the proportion of NE and PQ. Then max[P Q,N E] is transformed into a new matrix Ζ= [α · N E +(1 - α)· PQ]. When 0 ≤ α≤ 0.5,the path quality of the link is the main factor in selecting the controller locations. But when 0.5≤α≤1, CPS depends on the efficiency of the node itself.

In CPS, the quantity of required controllers in the network is determined precisely through iterating parameters and comparing node states. Meanwhile, we introduce the balance factor β to further optimize the controller locations, which could effectively prevent too centralized or too decentralized distributions of the controllers, as shown in Eq. (20).

The CPS algorithm is presented as followings. Firstly, we need to collect the network information and set the upper and lower bounds of the quantity of controllers (Line1 to 2). Then the interval of α is [0,1], which is split into k subintervals (Line 3), and we compute (N Ei, P Qi,α) for the corresponding node.The results are stored into Ζαi(Line 5), which can form the matrix Z (Line 6). The maximum value of each row in Z is selected to construct the column matrix Z*and we need to compute maxZ (Line 7 to 8). The t is a variable for counting the marked nodes, and C*is the set of pre-deployment nodes of controllers. At the beginning of iteration, t=0 represents no node is marked as the pre-deployment nodes and C*is empty. Along with increasing of iteration times, the suitable nodes are added into C*(Line 9 to 13). We search rational t between the upper and lower bounds by the dichotomy,and introduce β to implement iterative adjustment (Line 14 to 19). Finally, we get the set of controllers and the set of controller locations(Line 20 to 21). The pseudo-code of CPS algorithm is shown in Algorithm 1.

Theorem 2. CPS algorithm is convergent.

Proof. CPS includes three parts: con-structing Ζ, selecting C*and optimizing the controller locations. In the initial phase, each iteration of CPS will dynamically change α to get the corresponding Ζ values. If the current iteration does not get the maximum value, the controller deployment nodes will be increased,and [kmin,kmax] is further implemented finegrained division. After the adjustment is over,Ζαiis compared withmaxΖ to remove the nodes with the low efficiency. Considering the influence of β, we define C*as the set of the removable nodes. Therefore, for a given network, the whole algorithm will get C under the limited number of iterations, which has the property of convergence. Meanwhile, through increasing the initial threshold to kmin, we also speed up the convergence rate of CPS.

The complexity analysis of CPS. At the beginning of CPS, it records the states of nodes and links, so the complexities are O(n)and O((n-1)2), respectively. The complexity of constructing Ζ is O(n·k). O(t) is the complexity of forming C*. The complexity of building CL is O(k). Thus, the total complexity of the whole algorithm is O(n2). Due to the range of selected nodes is limited and the operation methods are simple, the algorithm is real-time and effective.

4.2 Multiple domain partition(MDP)

Based on the output of CPS, we improve K-center approach and design MDP to achieve max[CLBR] and plan domains reasonably.Through implementing node clustering,K-center aims to minimize the maximum distance from the node to its nearest controller. However, K-center doesn’t consider the flow request rates of switches. In MDP,based on the node attractability (definition 2),the switches are allocated for the controllers with the determined deployment locations.Meanwhile, we set the redundancy function γ(cj) in Eq. (21), which could ensure that the controller reserves a portion of the processing capacity to handle traffic burst and realize controller status synchronization. So, we get|CLBR-CLBR*|≤ ε, where ε is the difference of controller load balancing rate between the actual condition and the ideal condition. The smaller ε, the more balanced controller loads.Finally, there is max[CLBR] in the network.

Algorithm 1. CPS.Input: Network topology G=(V,E)Output: Set of controller locations CL 1: Collect the information of nodes and links 2: kmin=1, k n max=3: Initialization k=kmin 4: for (α α α α 0; 1; 1k)5: Compute Z NEPQ=≤=+αi ←( , ,)i iα 6: Ζ=Ζ Ζ Ζ Ζ[ , , ,..., ]α α α α i i i i= = = = × +0 1 2 1[ ( 1)]k k n k[max ,max ,...,max n]T 8: Compute 7: Ζ= Ζ Ζ Ζ*1 2 max (1) max Ζ= · Ζ n∑i=1 n i 9: while (i≤n)10: if max max Ζ ≥ Ζ i 11: t++; C C c* *= ∪{ }t,vi 12: endif 13: endwhile 14: if k t k k＜ ＜( + )2 15: then k++, return Line 4 16: ∃ ∈min min max c c C iv jv, ,m n,* and (0 ) ( 2 )＜ ＜ ＞ β l l mn mn β∪17: C C c c* *= { , }iv jv, ,m n; t=(t+k )2 max 18: return Line 10 19: endif 20: C←C*21: Get the set of controller locations CL

CPS algorithm is described as followings.Firstly, all controllers are initialized, and the average number of switches in domain is τ(Line 1). We build the node attractability matrix for each controller node Then, controller locations are updated by transforming matrix and filtering nodes (Line 5), and we remove all duplicate nodes in the domain. (Line 6 to 14). Next, we further detect whether there are isolated nodes that do not belong to any domains. If so, the isolated nodes are allocated into the nearest domain with light loads. (Line 16 to 19). After comparing with CLBR*, the algorithm returns Line 6 or directly outputs the result of the domain planning (Line 22).The pseudo-code of MDP algorithm is shown in Algorithm 2.

Algorithm 2. MDP.Input: Set of controller locations CL Output: The domain planning G=∪ D k j=1 j 1: Initialization ∀ ∈ =j,Dj{}φ,τ=INT(nk)2: for (j j kj c C 1, ; )3: Construct N [ , ,...,]=≤++A NA NA= v v c c j j j 121×(-)nk 4: Transform matrix by descending order: NA NA*j j←5: Select τ nodes in front from NA*j: F NA j j, , ∩ φ)7: Η=← *6: while (∀ ∈ ≠cc CF F p q p q p ∑Bp λ, Η =i q ∑Bq λi 8: case ( ( ) ) ( ( ) )Η ≥ ·Φ Η ≥ ·Φ p p q q γc ∩ γc 9: then F F{ }← {∩}10: case ( ( ) ) ( ( ) )p p p q← F∩F , F F F F q q p q Η ≥ ·Φ Η ≥ ·Φ p p q q γc ∪ γc 11: then F F F F← {∩}12: case Η ＜Η ＜p p p q← {∩} or F F F F q q p q p q i∑Ηq λ 13: then Fq q p q←F{F ∩F} τ++ return Line 5 14: endwhile 15: SM F j← j, G D∗=∪k j=1 j 16: while (G*≠G)17: Λ= ∈Λ GG∗,vi , nearest domain of vi: N D i={ }18: D N j i j∈ ∪min∑λ→D=D v j j∪{i}19 : endwhile 20: if | |CLBR-CLBR*＜ε 21: then return Line 6 22: else Output maxCLBR,G←G∗23: endif

Table II. Topology information.

The complexity analysis of MDP. Firstly, we will construct the node attractability matrix, and its complexity is O(n·k). Then,the complexities of checking duplicate nodes and isolated nodes are O(k2-k) and O(Λ),respectively. But O (Λ) ≤ O(k ). Therefore, the total complexity of MDP is O(nk). The data processing only requires to carry out linear operation, and the algorithm will converge to a stable condition finally.

Therefore, the complexity of solving the objective function is the sum of CPS’s complexity and MDP’s complexity, which is O(n2+ nk).

V. EVALUATION AND ANALYSIS

5.1 Simulation setup

5.1.1 Experimental platform

We select Opendaylight [28] as the experimental controller. Mininet [29] developed by Stanford University is set as the test platform.Opendaylight is programmed by Java and supports multiple versions of OpenFlow protocols. To ensure the smooth operation of the experiment, we deploy Mininet and Opendaylight on the two physical devices, which have the same hardware configurations (Intel Core i7 3.3 GHz 8 GB RAM). The operating system of the device is Ubuntu 14.04 LTS.

5.1.2 Topology selection

In order to make the experiment more representative, we select the topology models from Topology Zoo [30], which is established by the Australian Government and the University of Adelaide together. The information of selected topologies is shown in Table 2, where the node degree metric represents the average number of links connected to one node.

5.1.3 Parameter setting

In this paper, we assume the flow characteristics of the switches are similar with [20], and the average flow rate is 500 KB/s. The controllers have the same processing performance,and the maximum processing capacity of the single controller is 5MB/s. The range of link bandwidth is between 10MB/s and 15MB/s.The failure probability is independent for each device [36]. Meanwhile, we set ε=0.1 in advance [37].

5.2 Simulation analysis

5.2.1 Simulation comparison

To illustrate the performance of RLMD, we compare it with Random Deployment (RD),K-center strategy [13] and Survivor strategy[24] in the experiments.

• Random Deployment (RD): it selects the locations of controllers in the network randomly, and each controller has the same number of switches.

• K-center: it implements clustering according to the distance between nodes, and sets the clustering centers as the locations of the controllers.

• Survivor: it explores path diversity and considers capacity-awareness proactively for the controller deployment. Besides, the switches are distributed to the nearest controller in Survivor.

• RLMD: it considers controller reliability and load balancing rate to deploy controllers.

The evaluation metrics of the experiments contain: (1) the number of controllers; (2)connection interruption probability; (3) the average delay; (4) controller load balancing rate.

5.2.2 The number of controllers

Based on the different topologies in Table IV, we compare the number of controllers in four strategies, and the experimental results are shown in figure 2. When the scale of the network is small, the four strategies have the same requirements for the controllers (2 controllers). As the network continues to expand,the number of controllers increases gradually.From Abilene with 12 nodes to Tw with 96 nodes, the increment of controllers is the most obvious in RD. On the whole, the growth rates of controllers are similar in K-center and Survivor. However, in Germany and Columbus, Survivor remains fairly constant, while K-center has a great change. This is because the controller deployment in Survivor is related to paths. Though the number of nodes is different in Germany and Columbus, the number of links is almost equal in both two topologies. So the controllers in Survivor stay the same (7 controllers) in both Germany and Columbus. Compared with the above three strategies, RLMD computes the node efficiency and path quality, and introduces the weight parameter to implement iteration in a dichotomy way. Moreover, balance factor contributes to optimize the locations of the controllers.Therefore, no matter in small-scale network or large-scale network, RLMD can deploy controllers more reasonably, and the number of required controllers reduces about 22.1%.

5.2.3 Connection interruption probability

Considering the node reliability and link failure, we introduce connection interruption probability (CIP) of the network in Eq. (22),

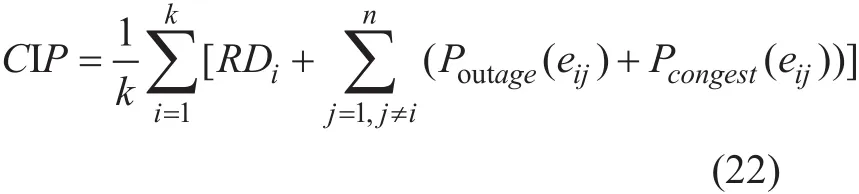
where the computations of RDi, Poutage(eij),and Pcongest(eij) are based on Eq. (2), Eq. (8)and Eq. (9), respectively.

punitis set as the probability of link failure per 10 kilometers. Specifically, we select Abilene and Germany as the experimental topologies, and verify the effect of different failure probabilities on CIP. The simulation results are shown in figure 3 and figure 4.

Fig. 2. The number of controllers for different strategies.

In figure 3, the range of punitis [0.01,0.1],and the simulation results of Abilene and Germany are shown in figure 3(a) and figure 3(b),respectively. When punit=0.01, the values of CIP are basically close to 0 for all strategies.With the increasing of punit, CIP presents the linear increasing trend. However, due to RLMD considers more comprehensively (reliability and load balancing), its CIP is better than the other strategies. When punit=0.1, RD has the maximum CIP, K-center takes the second place, Survivor is the third and RLMD is the least.

We adjust the maximum value of punitfrom 0.1 to 1, and the experimental result is shown in figure 4. In terms of the increasing rate of CIP in Abilene (Fig. 4(a)) and Germany (Fig.4(b)), RD is the fastest, K-center takes the second place, Survivor is the third, and RLMD is the slowest. This is because RD doesn’t consider network situation (nodes and links)during controller deployment, which causes controllers are easy to malfunction. If the control path breaks down, the transmission of packets will be interrupted, and CIP reaches to the maximum value quickly in RD. K-center considers the shortest link between nodes,while Survivor regards the maximum quantity of links connected with the nodes, and both of those could prevent the connection interruption to some extent. Integrating the node

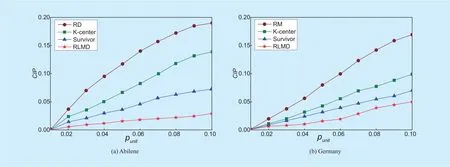
Fig. 3. The effect of punit (0.01 to 0.1) on CIP.

Fig. 4. The effect of punit (0.01 to 1) on CIP.

efficiency and path quality, RLMD selects the nodes with high reliability to deploy controllers and ensures the links connected with controller nodes have the lower failure probability, so it could reduce the impact of connection interruption on the network effectively. In general, the growth trend of CIP is the slowest in RLMD. In particular, when punit=0.03, as shown in dotted line in figure 4(b), there are the maximum differences for CIP in four strategies.

5.2.4 The average delay

In the network, the average delay between devices includes three parts: the forwarding delay df, the controller processing delay dpand the transmission delay dt. In this experiment,we set df=0.05m s and dp=0.01m s. Moreover, dtincreases 1ms every 10 kilometers.Based on Abilene and Germany, we change the number of controllers and observe the variation of the average delay under different strategies. The experimental results of two topologies are shown in figure 5(a) and figure 5(b), respectively.

Firstly, in figure 5(a) and figure 5(b), as the number of controllers increases, the performance of flow processing of the network has improved, and the average delay of the four strategies presents the decreasing trend. Compared with the other three strategies, RLMD adopts the progressive design to select reliable controller locations and balance the distribution of switches, so its average delay declines quickly. After controllers appear redundant(the total number of controllers is more than 8), the downward trend of the average delay is basically stable.

Fig. 5. The average delay for different strategies.

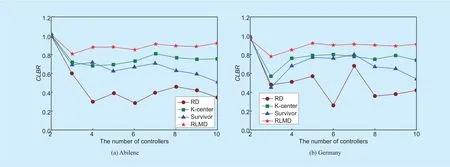
Fig. 6. The values of CLBR for different strategies.

Next, based on the same number of controllers, we also make a vertical comparison for four strategies in both figure 5(a) and figure 5(b). When the number of controllers is less, the average delay of Survivor is close to RLMD’s. With the increasing of the controllers, Survivor places emphasis on the length of control path, but ignores the load balancing,and the optimization of the average delay of RLMD is obviously better than Survivor’s at this moment. Afterwards, network is deployed more controllers. The average delays of Survivor and K-center are similar, but their optimizations are still poor compared with the result of RLMD. Through changing ε (ε=0.05 and ε=0.01), we repeat this experiment to perform the fine-grained comparison of the average delay. However, the improvement of experimental precision is limited compared with ε=0.1, which is defined beforehand.Therefore, ε=0.1 has been able to reflect the optimization results of the average delay for different strategies effectively.

5.2.5 Controller load balancing rate

In this experiment, we apply the controller load balancing rate CLBR (definition 4) to evaluate the distributions of the controller loads. The higher CLBR, the better performance of load balancing. Based on Abilene and Germany topology, the node traffic follows Poisson distribution [38], and the total traffic is in the relatively steady state in the network.

Through changing the number of controllers, we record the values of CLBR for different strategies. The experimental results of two topologies are shown in figure 6(a) and figure 6(b). Due to the limited controller capacity,when the network only deploys 2 controllers,each controller is in overload state and the control resources are fully exhausted, so the values of CLBR are the highest. As the number of controllers increases, the random selection makes RD have the low and unstable CLBR generally. K-center only performs nodes clustering based on the link distance regardless of network traffic, then CLBR maintains in about 0.8. Survivor considers the connectivity and the controller capacity to deploy controllers.However, the path diversity decreases with the increasing of controllers, which causes that the alternative controller locations are insufficient. So CLBR declines gradually in Survivor. Based on the reliable deployments of controllers, RLMD computes the node attractability to allocate the switches. Meanwhile, it introduces the redundancy function to prevent the burst traffic of controllers. Therefore, the value of CLBR remains above 0.9 averagely in RLMD, which increases by 17.5% (Abilene)and 19.4% (Germany) at least compared with the other three strategies.

VI. CONCLUSION AND FUTURE WORK

In the distributed SDN network, this paper proposes RLMD strategy to improve the reliability of the control plane and balance controller loads. By modeling the multi-controller network and defining the relevant parameters for RLMD, we design the corresponding algorithms, which include CPS and MDP. Finally,the simulation shows that RLMD could adapt the different network topologies and have some merits of saving the controllers, improving the control plane reliability, reducing delay and balancing controller loads.

In the future work, the evaluation should be extended to consider specific situations,such as dynamic load balancing and switch migration. Additionally, more aspects could be explored to further improve load balancing performance of the controller.

ACKNOWLEDGEMENTS

This work was supported in part by This work is supported by the Project of National Network Cyberspace Security (Grant No.2017YFB0803204), the National High-Tech Research and Development Program of China(863 Program) (Grant No. 2015AA016102),Foundation for Innovative Research Group of the National Natural Science Foundation of China (Grant No.61521003). Foundation for the National Natural Science Foundation of China (Grant No. 61502530). Specially, I sincerely appreciate my girlfriend Tongtong (sha niu), thank her love and concern.