Performance Analysis of Physical Layer Security over α-η-κ-μ Fading Channels

Shaobo Jia, Jiayan Zhang, Honglin Zhao＊, Yao Xu

Communication Research Center, Harbin Institute of Technology, Harbin 150001, China

Abstract: In this paper, we consider the secure data transmission over α-η-κ-μ fading channels, which are recently proposed to encompass nearly all the well-known statistical models adopted in the literature. In particular,we address the secrecy performance in terms of the average secrecy capacity (ASC) and the secrecy outage probability (SOP), for which novel analytical expressions are derived. Simulation results verify the analysis and demonstrate the impact of the physical parameters on the secrecy performance of this new channel fading model.

Keywords: Physical layer security, α-η-κ-μ generalized fading channels, average secrecy capacity, secrecy outage probability

I. INTRODUCTION

Due to the openness of the wireless media, the explosive growth of mobile traffic and newly emerging wireless applications introduce different security risks in the wireless communications. Traditionally, secure communication is achieved through complex cryptographic technologies using secret keys [1-2]. However,these cryptographic approaches are based on the assumption the eavesdroppers have limited computational resources, and are thus not perfectly secure. As a complementary method,physical layer security (PLS) is envisioned as a promising technique implemented at the physical layer without the need for complex upper-layer encryptions. By smartly exploiting intrinsic randomness of the communications media, PLS has been developed based on an information-theoretic viewpoint. PLS work was pioneered by Wyner, the fundamental notion secrecy capacity which was defined as the difference between the main link and the wiretap link was introduced in [3]. The secrecy capacity of the scalar Gaussian wire-tap channel was analyzed in [4]. This result was generalized to the wireless fading channel in[5] and [6].

Recently, considerable attention has been focused on the secrecy performance analysis in digital systems over fading channels (e.g.,[7-15], and the references therein). In [7], the exact expressions for both the ASC and the SOP over correlated Rayleigh fading channels were derived in the form of infinite series. The asymptotic SOP over correlated log-normal fading channels was evaluated in [8]. The strictly positive secrecy capacity (SPSC) over Weibull fading channels was studied in [9].The lower bound of SOP and the SPSC over κ-µ fading channels were presented in [10].The ASC and asymptotic ASC over α-µ fading channels were derived in [11]. The PLS for single-input single-output (SISO) and single-input multiple-output (SIMO) generalized-K fading channels was investigated in[12] and [13], respectively. Several optimal relay selection schemes were proposed in [14]and [15] to improve the PLS in wireless cooperative networks and cognitive radio networks,respectively, and the secrecy performances in terms of intercept probability or SOP were then analyzed.

However, any fading model mentioned above is only applicable to a certain usage scenario, thereby lacking the flexibility to account for disparate propagation mechanisms as those characterized in future communication networks which accommodate many emerging scenarios, for instance, mobile-to-mobile, device-to-device, body-centric fading channels,and others. In an effort to fill such a gap, the α-η-κ-μ fading distribution was proposed in[16] recently as an excellent alternative for new practical wireless applications. This new fading model is rather an attractive proposition, in addition to offering far better and much more flexible representations for new applications, it seems to encompass nearly all the well-known statistical models, such as κ-µ[10], α-µ [11], and their inclusive ones (e.g.,generalized-K [12]). So far, there are very few works exploring the system performance over α-η-κ-μ fading channel. In [17], channel capacity was studied under four different transmission techniques.

To the best of our knowledge, the performance analysis for secure data transmission over α-η-κ-μ general fading channels has not been yet addressed in existing works. Motivated by the aforementioned observation, the secrecy performance over α-η-κ-μ fading channels is investigated in this paper. The main contributions of this paper are summarized as follows:

• We derive a unified analytical framework

for the computation of the ASC and the SOP over α-η-κ-μ fading model. The new derived results can be exploited to analyze the secrecy performance of a tree of fading models with a combination of the corresponding parameters. Moreover, our results are more applicable to practical communication scenarios where nonlinearity of medium, power of the scattered waves, power of the dominant components, and multipath clustering are addressed.

• In order to explicitly examine the performance in the high SNR region, the exact expression of asymptotic ASC is derived.It is proved that the ASC ceiling is created when the average transmit power goes to infinity.

• The accuracy of the analysis and the impact of parameters on the secrecy performance of α-η-κ-μ fading model are verified through Monte Carlo simulations.

The remainder of this paper is organized as follows. We describe the system model in section II. In section III, we derive the exact expressions for the ASC, asymptotic ASC and SOP, respectively. Numerical results in section IV are presented to illustrate the proposed results. Finally,we conclude this work in section V.

In this paper, the authors present a unified analytical framework for the computation of the ASC and the SOP over α-η-κ-μ fading channels.

II. SYSTEM MODEL

2.1 A overview of the α-η-κ-μ fading model

The α-η-κ-μ fading model describes a signal composed of multipath clusters, arbitrary dominant components, arbitrary multipath powers, and arbitrary number of multipath clusters for in-phase and quadrature components propagating in a nonlinear environment.Such a nonlinearity is in the form of a power parameter α＞ 0, so that its received signal envelope, R, may be expressed in terms of the in-phase and quadrature components of the fading signal [16, eq. (9)]

where Xiand Yiare mutually independent Gaussian processes with zero mean and variancerepresents the expectation operator; λxiand λyiare, respectively, the mean values of the in-phase and quadrature components of the multipath waves of cluster i; µxand µyare the number of multipath clusters of in-phase and quadrature components, respectively. The probability density function (PDF) of the envelop R is defined in [16, eq. (29)] as

where coefficient clis a key variable related to the parameters α, η, κ, µ, p, q, and rˆ, which can be obtained with the aid of [16, eq. (15),eq. (30), eq. (31)]. rˆα=is defined as the mean of E(Rα), rˆ is a α-root mean valueis the ratio of the total power of the in-phase and quadrature scattered waves of the multipath clusters;is the ratio of the total power of the dominant and total power of scattered waves,µ=(µx+ µy)2 is the total number of multipath clusters; p=(µx/µy) is the ratio of the number of multipath clusters of in-phase and quadrature signals;the ratio of two ratios: the ratio of the power of the dominant components to the power of the scattered waves of the in-phase signal and its counterpart for the quadrature signal.Solving these equations for rˆ, η, κ, µ, p and q, then

Fig. 1. System model demonstrating a source transmit (Alice), a desire receiver (Bob), and an undesired eavesdropper (Eve).

Note that, α, η, κ, µ are the fading parameters, where α affects only the resulting signal envelope, and η, κ, µ independently have an influence on its in-phase and quadrature components. p, q are the imbalance ones. It is worth highlighting that the α-η-κ-μ distribution unifies nearly all the statistical models proposed in existing public works. Hence a number of models, such as α-µ (κ→ 0,η=p)[11] and κ-µ (α=2, η=p) [10], can be viewed as special cases of it [16].

2.2 System model

In this paper, we consider the classic Wyner’s wiretap model [3], wherein a legitimate transmitter Alice (A) exchanges confidential information with a legitimate receiver Bob (B)in the presence of eavesdropping performed by an eavesdropper Eve (E), as shown in figure 1. We assume that both the main channel(Alice→Bob) and eavesdropper channel(Alice → Eve) undergo independent α-η-κ-μ general fading. The received signal at Bob and Eve can be respectively expressed as

III. PERFORMANCE ANALYSIS OF SECURE DATA TRANSMISSION OVER α-η-κ-μ FADING CHANNEL

In what follows, we focus our attention on the secrecy performance analysis over α-η-κ-μ fading model, including the ASC and the SOP.Then, novel analytical expressions are derived for these two secrecy performance metrics.

3.1 Average secrecy capacity analysis

We consider the active eavesdropping scenario, where the perfect channel state information (CSI) of both the main channel and the eavesdropper channel is available at Alice. In such a case, perfect secrecy can be guaranteed by keeping the achievable secrecy rate Rsless than the equivocation rate of Eve Re[20].Here, the maximum achievable secrecy rate Cs= Reis our main focus, which is referred to as secrecy capacity. According to [19], the instantaneous secrecy capacity is characterized as

where ln(1+γB) and ln(1+γE) are the capacity of the main channel and eavesdropper channel, respectively. ASC, which is characterized as the average of the secrecy capacity over γBand γE, is essentially a fundamental metric to evaluate the secrecy performance in such a scenario. Mathematically, ASC is given by[19]

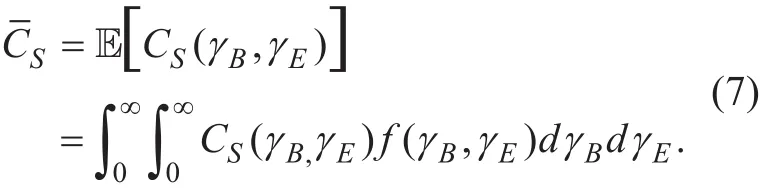
Since both γBand γEfollow independent α-η-κ-μ distributions, the joint PDF of γBand γEf (γB,γE) =fB(γB) fE(γE). Afterwards, by plugging (6) into (7),can be rewritten as

Using the definition given in [18, eq.(8.970.1)], the Laguerre polynomials(x)can be rewritten in terms of series expansion as

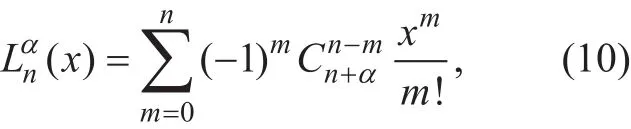
Substituting the PDF of γEand the CDF of γBinto I1, after some algebraic manipulations,we can obtain

for ease of description. With the aid of[21, eq. (07.34.03.0228.01)] and [21, eq.(07.34.03.0456.01)], the logarithm function and the exponential function can be written in terms of Meijer’s G-function as

where (a) holds from [22, eq. (1.59)]. Resorting to [23, eq. (2.3)], (15) can be written in terms of the generalized (bivariate) Fox’s H-function as

The church bells were ringing, and from the high towers sounded a flourish of trumpets105; and soldiers, with flying colors and glittering bayonets, lined the rocks through which they passed

Following a similar approach to that we derive I1, the exact expression of I2can be computed as (18) shown in the next page.

where

Now, with the help of [17, eq. (7)]. I3is obtained as (19) below

Substituting (17), (18), and (19) into CS, the exact expression of ASC is finally obtained.

In order to gain more insights into the sececy capacity performance, we hereafter derive the expression of asymptotic ASC in the high SNR region. On condition thatholds whengoes to infinity (i.e., high SNR), Hk(k∈{B,E}) are random variables of the fading power gains,and=E[Hk] are the average power gains.Substituting the PDF of γi(i∈{B,E}) into(7), and after series of mathematical manipulations, the asymptotic ASC can be further derived as (20) at the bottom of this page,

where

Then, utilizing the substitutionandcan be further derived as(23),

where

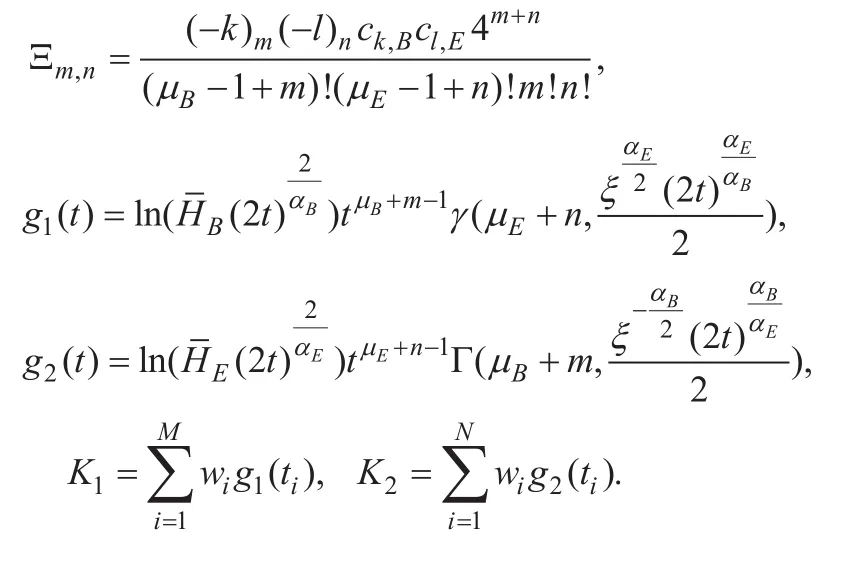
and (a) follows from the Gaussian-Laguerre integration formula [25, eq. (25.4.45)], with wiand tirepresenting the abscissas and weight factors.

3.2 Secrecy outage probability analysis

We concentrate our attention on the case where the eavesdropper is totally passive, i.e.,the CSI of eavesdropper’s channel is unavailable at Alice. While in such a case, perfect secrecy can not be guaranteed, and hence,the concept of outage probability has to be invoked. Here, we adopt the notion of secrecy outage probability, which is an important and well-known performance measure to evaluate the secrecy performance in such a scenario.The secrecy outage probability, referred to as SOP, is defined as the probability that the instantaneous secrecy capacity Csis less than a target secrecy rate Rs(Rs≥0). Mathematically,it can be expressed as

At present, it is rather difficult to directly derive (25) due to the complicated integral of polynomial power that involved. Therefore,for the case where γE→ ∞, the lower bound of SOPis derived as [10], [11], [12]

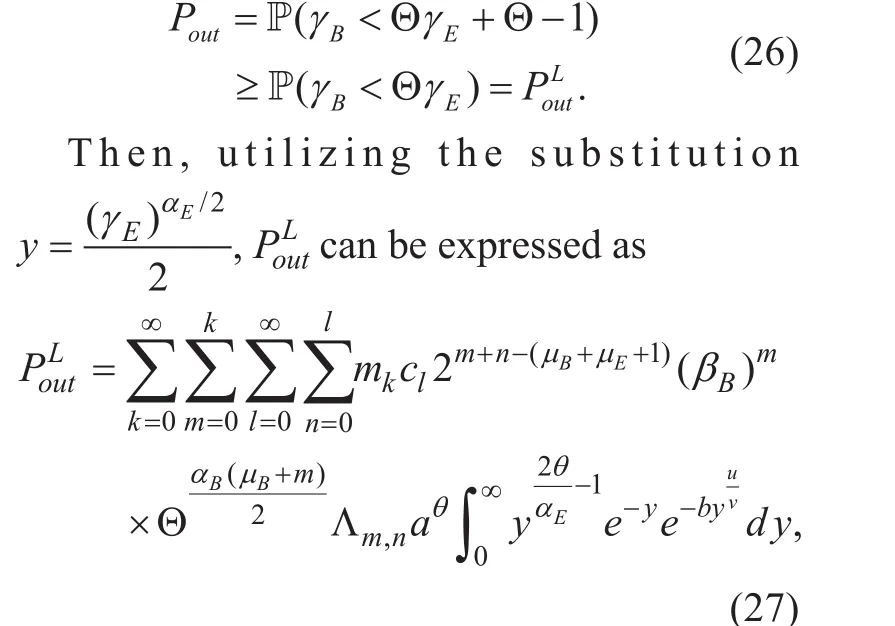
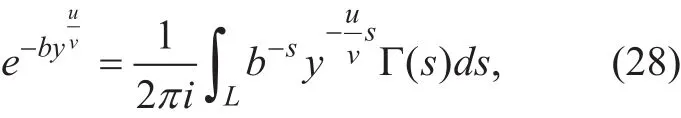
where L is a suitable contour. With the aid of[18, eq. 3.326.2], the integral term of (27) can be attained as

Using the multiplication formula given in[25, eq. 6.1.20], we can rewrite the Gamma function in (29) as

Substituting (30) into (29), we can further evaluate I as

where (a) holds by using the definition of the Meijer’s G-function. Substituting (31) into(27),an be finally obtained as (32) below.

IV. SIMULATION RESULTS

In this section, theoretical analysis and simulation results are presented to verify the analytical deviations. The main simulation parameters are set as αB=αE=α= 2, ηB=ηE=η=3, κB=κE=κ= 1, µB=µE=µ= 2, pB=pE=p= 1, qB=qE=q= 1, and Rs= 1 nat/s/Hz. Since the exact expressions of the ASC and SOP are derived in the form of infinite series, the number of terms is selected under a given accuracy 10-4.As already indicated in [16], the computation-al burden for performing the numerical results varies with the values of the parameters, while in our simulations, the number of terms is no bigger than 18 for all considered cases. It is clearly shown that the theoretical analysis and simulation results are in an excellent match in all the figures.

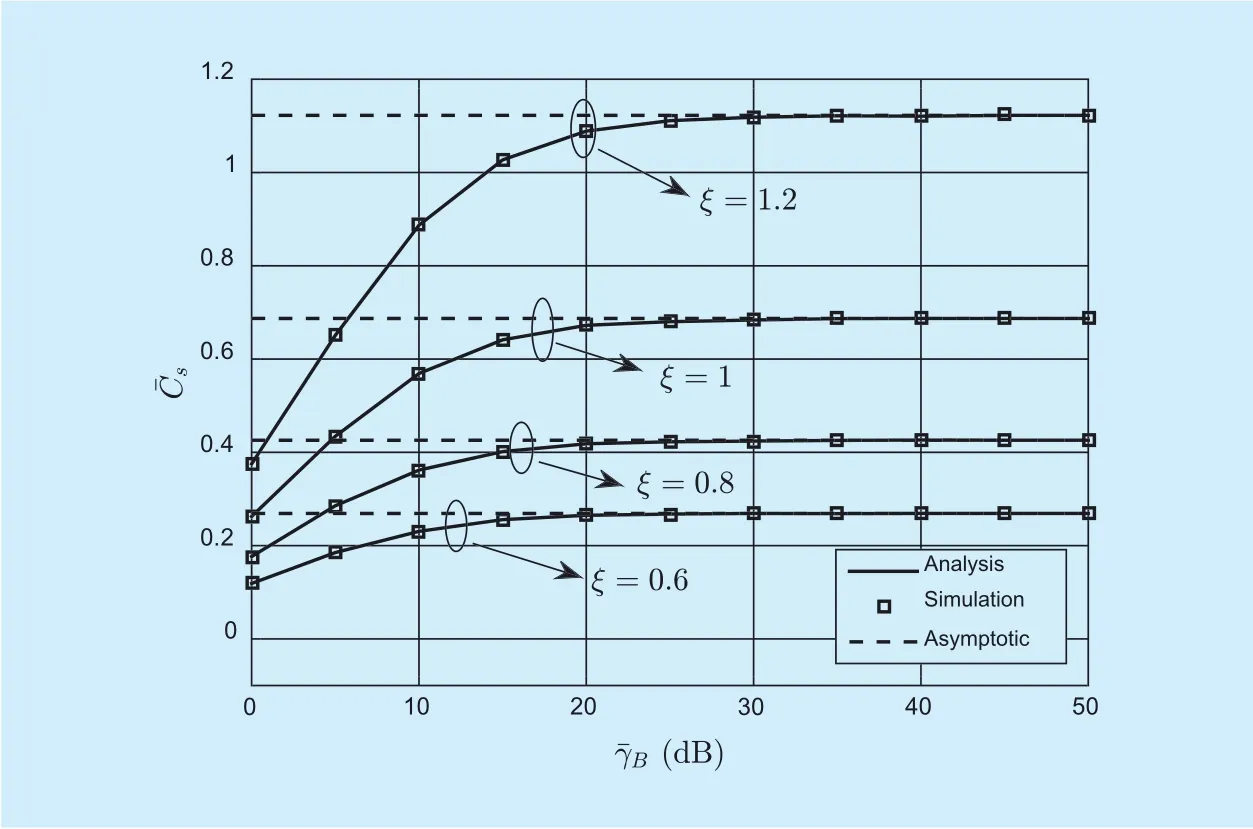
Fig. 2. ASC versuswith different ξ.

Fig. 3. The lower bound of SOP versus with differentγE.

Fig. 4. ASC versus γB with different channel parameters (=10dB).

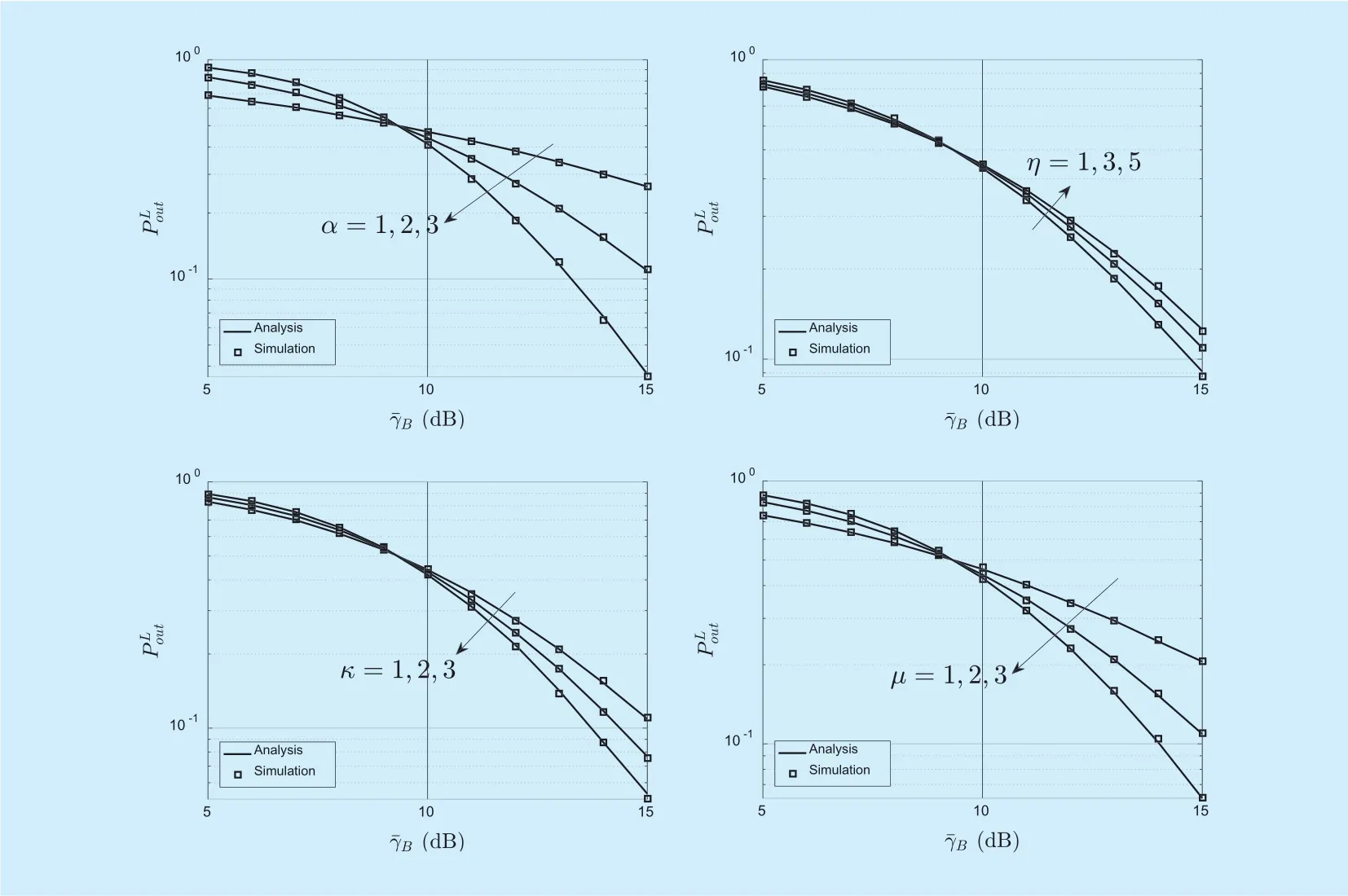
Fig. 5. The lower bound of SOP versus with different channel parameters (=5dB).

In figure2, we present the ASC againstover α-η-κ-μ fading channels for different ξ values. As expected, the overall secrecy performance improves while increasing the average SNR of the main channel. This is due to the reason that a higherindicates a better secure channel condition for the main channel. We also plot the results of asymptotic ASC to make comparison with the ASC curves. We can see that the ASC curves with different ξ values approach a constant in the high SNR region. This is because, for a fixed ξ, increasingwill also increase, hence,this will not only increase the capacity of the main channel but also the information leakage rate to the eavesdropper. In figure 3, we evaluate the SOP againstover α-η-κ-μ fading channels for different. It can be observed that the secrecy performance for a loweroutperforms that for a higher, which is the average SNR of the eavesdropper channel.Fig. 4 and figure 5 depict the ASC and the SOP versusfor different parameters α, η,κ and µ, respectively. In order to examine the impact of the parameters independently, we propose to vary one of the parameters with the others fixed, it is clearly shown that the ASC and the SOP degrade while increasing α, κ,µ, and decreasing η, which is in accordance with [10], [11] and [12]. It is worthwhile to mention that, due to the generality of the α-ηκ-μ fading model, Bob and Eve can be readily interchanged with some well-known fading models such as Rayleigh, Nakagami-m, α-µand κ-µ models, and so on, which all appear as special cases of this fading models. Notably, while in our simulation results, the case where α=2, η=1, κ=1, µ=2 corresponds to the special case κ-µ fading, the case where α=2, η=3, κ=1, µ=1 corresponds to the special case η-κ fading.

V. CONCLUSIONS

In this paper, we have presented a unified analytical framework for the computation of the ASC and the SOP over α-η-κ-μ fading channels. The new derived results can be exploited to analyze the secrecy performance of a tree of fading models through adequately operating on the corresponding parameters, e.g., α-µ, κ-µ,and others. Both theoretical analysis and Monte-Carlo simulations have demonstrated that the ASC and the SOP degrade while increasing α,κ, µ, and decreasing η. We also have showed that an ASC ceiling is created when both the average SNR of the main channel and the eavesdropper channel are large enough.

ACKNOWLEDGEMENTS

The authors would like to thank the reviewers for their detailed reviews and insightful comments, which have helped improve the quality of this paper. This work was supported by the Fundamental Research Funds for the Center University of China under Grant HIT. MKSTISP. 2016 13.