Fast Secret Key Generation Based on Dynamic Private Pilot from Static Wireless Channels

Yu Huang, Liang Jin＊, Hongquan Wei, Zhou Zhong, Shengjun Zhang

National Digital Switching System Engineering and Technological R&D Center, Zhengzhou 450002, China.

Abstract: In static or quasi-static wireless channel environments, secret key generation(SKG) based on wireless channels is vulnerable to active attacks due to the openness and invariance of public pilot, especially man-inthe-middle (MITM) attacks, where attacker acts as a transparent relay to manipulate channel measurements and derive the generated keys. In order to fight against this attack, a dynamic private pilot is designed, where both private pilot and secret key are derived from the characteristics of wireless channels and private to third party. In static or quasi-static environments, we use singular value decomposition techniques to reconstitute the wireless channels to improve the randomness of the wireless channels. Private pilot can encrypt and authenticate the wireless channels, which can make channel state information intercepted by MITM attacker reduced to zero and the SKG rate close to that without attacks. Results of analysis and simulation show the proposed SKG scheme can withdraw the MITM attacks.

Keywords: dynamic private pilot; MITM attacks; secret key generation; wireless channels; physical layer security

I. INTRODUCTION

The advent of mass market devices, such as smart phones, wireless tablet computers, laptops, etc., accelerate the developing of wireless communication technique, which causes a scene that anyone can use any service in anywhere and anytime. Meanwhile, the development of wireless communication makes a lot of private business (such as electronic commerce, telemedicine, remote access service, etc.) done by remote operation instead of face to face. The reason that the wireless communication can provide these conveniences,is the characteristic of broadcast, which also provides chance to attack the wireless communication for eavesdroppers. Therefore, the wireless communication also brings more and more challenges to the security and privacy of current systems. Unfortunately, wireless devices are usually powered by batteries and have constrained computing ability such that some traditional cryptography methods (e.g.,Diffie-Hellman key exchange scheme [1]),whose performance relies upon computational hardness of problems, face severe challenges.

Exploiting propagation properties of radio channels in physical layer to design efficient secure transmission schemes has attracted wide research interests recently. This approach is referred to as physical layer security (PLS)[2-4], which is robust to more advanced passive and active eavesdroppers. PLS and conventional encryption techniques can provide a well-integrated security solution which can efficiently ensure the confidential and privacy communication data. As an alternative approach of PLS, secret key generation (SKG)based on wireless fading channel has gained considerable attentions recently [5-11], due to its attractive features of lightweight, universality and information-theoretic security. Gacs and Körner first introduced it in [5] and used later by Maurer in [6]. Ahlswede and Csiszár in [7] and [8] explored the generation of common randomness by two terminals, which is private to a third party. Now, it has developed into a reference technique for wireless security. Unlike other PLS methods, which directly use the artificial noise (AN)-aided beamforming [12] and non- orthogonal multiple access(NOMA) techniques [13] to ensure information, SKG first generate secret key from the wireless channels, then encrypts information with the generated secret key to make it secure.

In this paper, the authors explore fast secret key generation based on private pilot under MITM transparent forwarding attacks in static or quasi-static environments.

However, the requirement of high randomness implies the dilemma of bad key generation performance in static or quasi-static environments (SQSE). Indeed, it can be a common situation when WSN and Smart Home systems are considered, where the wireless channels are generally static or quasi- static. Previous works addressed this challenge by diverse domains [14-19]. Multiple-antenna was used to increase the secret key generation rate (SKGR)in [14]. Random beam-forming was used in MIMO systems to improve the SKGR [15-16].Helper was introduced to increase SKGR in[17].

However, current studies mainly focus on passive eavesdropping cases, where eavesdroppers located beyond the coherence distance from legitimate nodes, will obtain uncorrelated channel state information (CSI),and cannot get any information about the generated keys [7]. However, SKG is vulnerable to active attacks, especially man-in-the-middle(MITM) attacks [18-23], where a malicious third party secretly takes control of the communication channels between two or more endpoints to intercept the private information.MITM attack was firstly mentioned by Bellovin [18]. Now, MITM has become a reference attack in security community. In Verizon’s data investigation report [19-20], researchers showed that MITM attack is one of the most common type of security attacks. Frankel [21]described MITM attack as one of the major threats against network security. Aiming at the Hole 196 vulnerability, Mayank et al. combined stealth MITM and wireless denial-ofservice attacks to inject spoofed broadcast/multicast frames in Wi-finetworks [22]. Since 3G-WLAN gateway is frangible to the kernel upgrade attack, an MITM attack was presented on 3G-WLAN internetwork [23]. The MITM attack is a severe threat to SKG due to the openness of the wireless channels and public pilot, which gives the attacker ease of access and the capability to remain unnoticed. Eberz et al explored signal-based SKG protocols under MITM attack, where Mallory implements the attack by injecting signals [24].

In this paper, we explore a more intelligent MITM attacker, who implements its attack by transparently relaying the channel-training signals of legitimate users, which is difficult to be found by legitimate users. To the best of our knowledge, there is no study about this type MITM attack. In our previous works, we explored the SKG from fast fading wireless channel under MITM attack [25]. Here, we investigated fast SKG based on the dynamic private pilot under MITM attack in SQSE. The differences are that reference [25] explored the fast fading wireless channels, where the randomness of channel is enough to generate secret keys, while this paper explores the static channels, where the randomness is poor.Investigation finds that the MITM attacker can intercept all CSI passing through it when secret key is generated with a public pilot even in fast fading wireless channels (FFWC). To fight against this MITM attack, we design a dynamic private pilot, where the legitimate nodes first take the information authenticated by them and private from third party as seed information of the private pilot. Then, the legitimate nodes generate private pilot based on the seed information according to the re-quirements of private pilot design. Finally,both new seed information and secret key are dynamically derived from different characteristics of the wireless channels estimated with private pilot instead of public pilot. To improve the randomness of the wireless channels in SQSE, we use singular value decomposition(SVD) techniques to reconstitute the wireless channels (RWC). Compared with some stateof-the-art approaches, the dynamic private pilot can encrypt and authenticate the wireless channels, and make the CSI intercepted by the MITM attacker reduce to zero, which demonstrates the proposed SKG scheme can effectively withstand the MITM attack. Moreover, using the uniqueness and privacy of the wireless channels, the proposed SKG scheme can be easily extended to other agreements and systems.

The main contributions are summarized as follows:

• Investigation finds that the MITM attacker can intercept all CSI passing through it when secret keys are generated with public pilot. To fight against the attack, we design a dynamic private pilot, which can make the CSI intercepted by the attacker reduce to zero.

• We use SVD techniques to reconstitute the wireless channels in SQSE to improve the randomness of the wireless channels and fast generate secret keys.

• We use first approximation of Taylor expan

sion to make the equation of SKGR convex and introduce the iterative algorithm to optimize the power allocation and improve the SKGR under the total power constraint.The remainder of this paper is organized as follows: Section 2 outlines the system model and problem. The design of the dynamic private pilot is presented in Section 3. Section 4 introduces the proposed SKG approaches.Section 5 presents the performance analysis of the proposed scheme. Numerical results and discussion are showed in Section 6. Section 7 concludes the paper.

II. SYSTEM MODEL AND PROBLEM

2.1 System model

As shown in figure 1, a time-division duplex system considers a narrowband block fading point-to-point wireless communication link,which is operated in a discrete memoryless Rayleigh fl at-fading environment. Legitimate users Alice and Bob want to generate a shared secret key based on wireless channels in the presence of an MITM attacker Eve, who acts as a transparent forwarding relay between Alice and Bob to manipulate the wireless channels and deduce the generated key. Eve works in a full-duplex mode with simultaneous information reception and relaying [26]. Assuming that Eve is enough powerful to know the SKG agreements. Since Eve wants to intercept CSI and infer the generated secret key, it always follows the transmission agreements of system as a transparent relay without destroying the communications. Alice, Bob, and Eve have NA, NB, and NEantennas, respectively. We assumed that all the channels among Alice,Bob, and Eve are independent, and none of the users or the attacker knows the CSI at the beginning of the communication. The strength of the received signals passing through Eve is much more than the strength not passing through Eve. In other words, the wireless channels passing through Eve are considered as the main channels by Alice and Bob, which may appear when Eve lies in the main channels between Alice and Bob or Eve is a false base station with Alice (Bob) under her coverage.

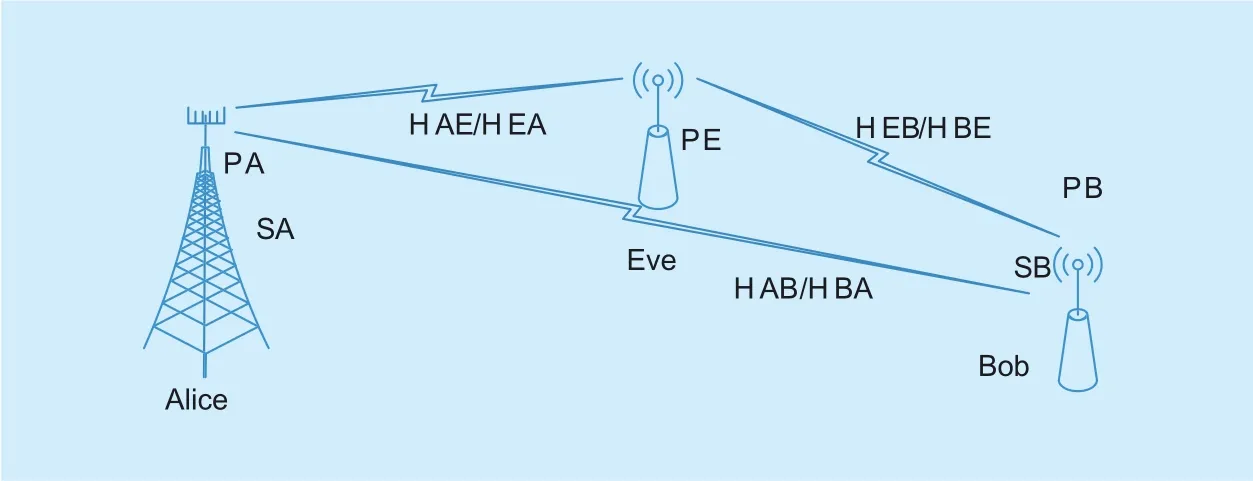
Fig. 1. System model.

2.2 Problems of the existing SKG scheme

Currently, to generate secret key according to wireless channels, the legitimate users obtain the channel parameters by reverse-link channel training and channel estimation, which is divided into 4 phases when Eve is considered.Assume that Alice transmits a pilot and Bob receives it in the first 2 phases, while Bob transmits a pilot and Alice receives it in the last 2 phases, where the process is almost same. We only discuss the first 2 phases and provide the corresponding results of the last 2 phases. All paths between Alice and Bob are equivalent to two uncorrelated paths with one passing through Eve. In addition, Eve knows nothing about the channels not passing through it.

Phase 1: In each time slot i, each Alice’s antenna transmits private pilot signal SAi,i=1,2,… NAto Bob during NAtime slots.We assume that SA=diag{SAi}, the ith column is the private pilot signal transmitted in time slot i. The received signals at Eve are given by

where µ∈[0,1] denotes power allocation factor to the channels passing through Eve; ρ is transmitting power; HAEand HBEare channel gains from Alice and Bob to Eve; NAEand NBEare the receiver noises at Eve; YAEand YBEare the received signals at Eve from Alice and Bob, respectively. These subscripts are also used in the following with the same meaning.

Phase 2: In time slot i, each Eve’s antennas relays the corresponding received signals in time slot i of Phase 1. The received signals at Bob and Alice are given by

Thus, Alice and Bob can estimate the channels as

Since all channel gains are independent normal distribution with zero means, as well as NA, NB, NAE, and NBEare independent Gaussian noises with zero means, according to[27], the SKGR can be denoted by:

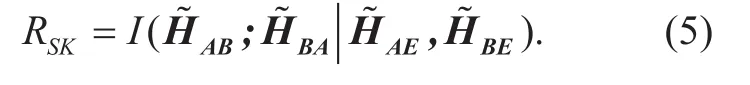
Theorem 1. The MITM attacker Eve can intercept all channel information passing through it, when secret keys are generated with public pilot.

Proof: According to (3), Eve can manipulate the wireless channels by the power amplification factors α and β to intercept CSI and derive part or all secret keys. For clarity,we assume there is only one equivalent path via Eve between Alice and Bob, which meansµ=1. Combining (3) and (4), the SKGR RSKwith public pilot can be denoted as

where PA, PBand PEare the transmitted power of Alice, Bob and Eve, respectively. Since Alice and Bob know PA-1SAand NA, meanwhile NA, NB, NAE,,and H~BEare independent, thusandare mutually independent, which makes I

Theorem 1 tells us that the MITM attacker Eve can intercept all CSI passing through it during the reverse-link channel training when the secret key is generated with a public pilot.Thus it is a serious threat to the SKG with public pilot. Indeed, Eve can intercept all channel information in most SKG schemes even if the wireless channels is fast fading.

III. PRIVATE PILOT GENTERATION

Aiming at the problems described in section 2,we discuss how to design the dynamic private pilot to withstand the MITM attack in this section.

Theorem 2. The CSI intercepted by Eve can be reduced to zero when private pilot A has constant spatial inner product e.g. A,where A is a pre-specified nonrandom NA× NAmatrix. The CSI intercepted by Eve can be reduced to zero when private pilot A has constant spatial inner product e.g. A, where A is a pre-specified nonrandom NA× NAmatrix.

Proof: Let Z=[Z1,Z2,… ,ZL] and Hidenote the sequences of Eve’s measurements and private pilots, respectively, and Hidenotes Eve’s channel matrix over the ith frame. The channel matrices are independent over each coherent fade interval, indexed by i, the joint conditional probability density of the observations factors into a product of marginal probability density is denoted as

Since Eve cannot estimate channels HAEand HBEbecause of the security of the private pilot, the product of marginal probability density can be written as

where INAis the NA× NAidentity matrix, and A denotes the magnitude determinant of square matrix A. When private pilot SSH=A=const has constant spatial inner product e.g.SSH=A=const, from the form of Eve’s likelihood function

we can directly deduce that Eve is absolute blindness to all CSI since this function is constant over the orbits { S:SSH=const}.This also implies that the CSI intercepted by Eve will be reduced to zero and the minimum probability of decoding error will be equal to one, if the private pilot with constant spatial inner product is transmitted over an uninformed Rayleigh-fading link. □

The process of the dynamic private pilot generation is described in table 1.

IV. THE PROPOSED SKG SCHEME

Although many works have extracted secret keys from wireless channels, a problem still needs to be addressed urgently. The problem isthat long successive identical or nearly identical secret key bit stream may emerge over SQSE. This bit stream can be predicted by the eavesdropper easily by predictable channel attacks, especially the MITM attacks. To overcome this problem and improve the randomness of the generated keys, we reconstitute the wireless channels using SVD techniques and then generate secret key combining the proposed private pilot with the reconstitution channels.

Table I. The dynamical private pilot generation.

Lemma 1. Let H be a NB× NAmatrix with NA≥ NB. Then, there exist orthogonal matrices U∈RNB×NB, V∈RNA×NA, and a diagonal matrix Σ =diag(,… ,σ )∈RNB×NAwithnσ1≥ … ≥ σn≥0, such that H=UΣVTholds.If σr＞ 0 is the smallest singular value greater than zero, the matrix H has rank r.

Observe that the matrix Σ can be in different forms because of the dimension of parameter matrix H. Hence for (full rank) H with NB≥ NA, we have

where NA× NAmatrix ΣNAincludes the nonnegative singular values and L=0∈R(NB-NA)×NA.

On the other hand, for (full rank) matrix H being of NA≥ NB, we obtain

where NB× NBmatrix ΣNBcontains, the nonnegative singular values and L=0∈RNB×(NA-NB).Of course, for both cases we have unitary matrices U∈RNB×NBand V∈RNA×NA.

In order to improve the randomness of the secret keys, channel matrix H is required of high variation and unpredictability. Here,we use SVD techniques to reconstitute the wireless channels in SQSE. For clearly understanding, we assume Alice generates random diagonal-matrix and reconstitutes the wireless channels, the process is described as:

① Alice and Bob estimate the wireless channels H with private pilot by reverse-link channel training and channel estimation as

② Alice and Bob make SVD of the estimated channelsandas

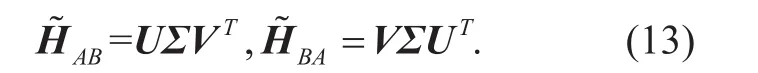
③ According to (10) and (11), Alice generates random diagonal-matrix ΣN′A, and reconstitutes the wireless channels matrix H as

④ After Alice reconstructing the wireless channels, it modulates the private pilot as

⑤ The equivalent channels are

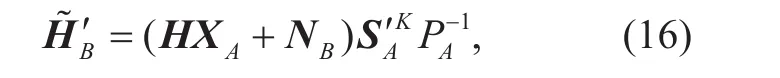
where NBis the received signals at Bob.

Remarks: Although H~ABand H~BAare unchanged, H~B′Ais randomly variable. Therefore,H~A′′Bis randomly variable, and Alice and Bob can generate secret key and update the private pilot from the equivalent channels or the received signals.

To improve the SKGR, Alice and Bob can also generate random diagonal-matrices ΣN′Aand ΣN′B, respectively. As soon as Bob receives the modulated signals XAfrom Alice, it transmits its modulated signals XBto Alice. Alice can obtain the two equivalent channels H~A′and′ reconstituted by Bob and itself since the wireless channels is invariable. In the same way, Bob can obtain the two equivalent channels. Therefore, they can generate secret keys according to the two equivalent channels.Alice and Bob can improve the efficiency of SKG by this approach because Alice and Bob can reconcile two samples at one time.

There are four approaches for Alice and Bob to generate secret keys based on the above proposed SVD channel reconstitution techniques. In the former two approaches, the secret keys are generated from the equivalent wireless channels and from the received sig-nals in the latter two approaches, which are described in the following. We assume that Alice and Bob have generated private pilot and know the CSI in SQSE. Thus, we only give the process of the proposed SKG. The first approach is described in Table 2.

Compared with FFWC, the reconstituted wireless channels vary every time when they are used, which is similar to “one time pads”and equivalent to the FFWC. The second approach is similar to the first one, and the differences are that only Alice or Bob reconstitutes wireless channels, the other estimates them. The results are that the SKGR of the second approach is only half of the first one.For simplicity, we do not give the specific process, which is similar to Table 2.

The latter two SKG approaches are from the received signals, and the third approach is presented in Table 3. The last approach is similar to the third, e.g. only one of Alice and Bob reconstitutes the wireless channels. Compared with SKG based on wireless channels, Alice and Bob do not need to estimate RWC when secret keys are generated based on received signals. Moreover, SKG based on received signals concentrates most of the computation and processing works on Alice (station), and ease the burden of Bob (user), which is suitable for the wireless networks, where wireless devices are powered by batteries and have constrained computing ability (such as WSN and Smart Home systems).

Of course, Alice and Bob can directly transmit the secret key by this approach, but the secret key bits are limited by the rank of the wireless channels. For (full rank) matrix H being of NA≥ NB(NB≥ NA), the SKGR of the former two approach can increase, at least, NA(NB) times compared with directly transmitting the secret key. Meanwhile, the computation complexity of directly transmitting the secret key is far higher than the above proposed approaches because of the SVD.

Compared with traditional SKG scheme,the proposed SKG scheme takes full advantages of the wireless channels to generateprivate pilot and secret key, which can ensure the security of the channel measure and SKG against the MITM attack. However, the proposed scheme has to first acquire the authenticated information between the transmitter and receiver by pre-installing, dynamic generation,secure transmission and so on, as well as adds the algorithm of private pilot generation.

Table II. SKG based on reconstitution wireless channels.

Table III. SKG scheme based on received signals.

V. PERFORMNCE ANALYSIS

5.1 Security analysis

As an important metric to measure the security of SKG schemes, SKGR RSK= Iis the reduction in uncertainty of S due to the knowledge of Y (vice inverse) when the leaked information is Z. In other words,I

quantifies the “amount of information” (in bits) obtained about one random variable,through the other random variable under the leaked information Z. If RSK＞0, Alice and Bob can generate secure keys, which cannot be intercepted by Eve. Form the definition of the MI, we can write the SKGR by

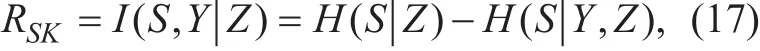
which shows Alice and Bob cannot generate secret key (e.g. RSK=0) in the following two cases: ① S is independent of Y; ② Z is complete correlation with either of S or Y. Case ①denotes what Alice and Bob obtain from the common source have nothing to do with each other, which may happen when the SNR is quite low. whereas case ② presents what Eve obtains from the common source is no less than Alice or Bob, which may happen when Eve obtain the common source with less noises than Alice or Bob, e.g. the above MITM attacker.

Theorem 1 only gives us the conclusion that the MITM attacker Eve can intercept all channel information passing through it. We analyze the reason combining the traditional SKG approaches, here. In general, Alice and Bob generate secret keys based on wireless fading channels using reverse-link channel training and channel estimation. However, the pilot used by Alice and Bob is public or invariable.With computer performance becoming more and more powerful, Eve can easily acquire the pilot. Once Eve obtains the pilot used by Alice and Bob, it can estimate the wireless channels between it and Alice as well as Bob. Thus, Eve can intercept all channel information passing through it even if the wireless channels are fast fading. There are some other SKG schemes,where secret keys are generated based on the techniques of multi-antenna, ultra-wide bandwidth, random beam-forming. However, once Eve acquires the pilot, it can intercept channel information passing through it. Unfortunately, this MITM attacker Eve exists in real life,such as the pseudo base-station, which has enough power to make that all devices under its coverage communicate passing through it. It means that almost all wireless channels passing through Eve. Once Eve obtains the pilot, all information will be intercepted by it.Thus, the MITM attacks is a serious threat to the wireless communication system.

In SQSE, when secret key is generated with the proposed dynamic private-pilot, Eve is not able to obtain private pilot since the private pilot varies and the wireless channels are reconstituted every time. This concept is similar to“one–time pads”. Since private pilot satisfies SK(SK)H= A =const, Eve cannot estimate the wireless channels passing through it, even if it can receive the signals transmitted by Alice and Bob, which means that it cannot intercept the generated secret key. If Eve wants to derive the generated secret keys by intercepting information, it is almost equivalent to the puzzle that Eve guesses the generated secret keys without any prior information. In conclusion, the proposed SKG approach is enough secure to fight against the MITM attacks.

5.2 The optimal solution of the SKGR

The speed of the SKG depends on the size of the SKGR. Thus, SKGR not only measures the security of the SKG, but also is an important measures of the system. We discuss how to improve the SKGR by optimizing the power allocation under the the total power constraint. We assume that private pilot vectors Si, i =1,2,… ,NAtransmitted by each antenna are dependent with each other withThe covariance matrix of the transmitted signals can be written by

where E[·] denotes expectation. Thus, CSSis positive definite-matrix. When the noises are ignored, the received signals can be written by

The covariance matrix of the received signals can be written by

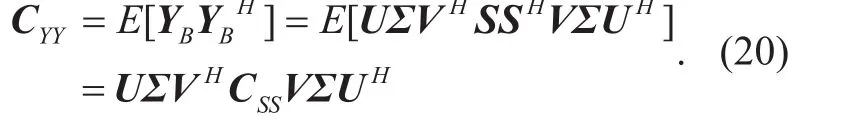
Thus, CYYis also positive definite-matrix.

If Alice uses V to modulate the transmitted signals S, e.g. X=VS, and Bob uses UHto demodulate the received signals, e.g. R=UHYB,the covariance matrix of R can be written by

In conclusion, if the transmitted signals S is independent Gaussian distribution with zero mean and variance CSS, e.g.S ～ N(0,CSS), so is the received signals with Y ～ N (0,U ΣCSSΣUH). Moreover, when Alice uses V to modulate the transmitted signals and Bob uses UHto demodulate the received signals, the signals R is also independent Gaussian distribution with zero mean and variance CRR, e.g. R ～ N(0,Σ CSSΣ), the elements of R are mutually independent, which can be used to generate secret key.

To improve the performance, we take a multi-antenna user as the MITM attacker Eve in the system. Thus, Alice and Bob can know all the channel gains. In SQSE, the SKGR can be written by

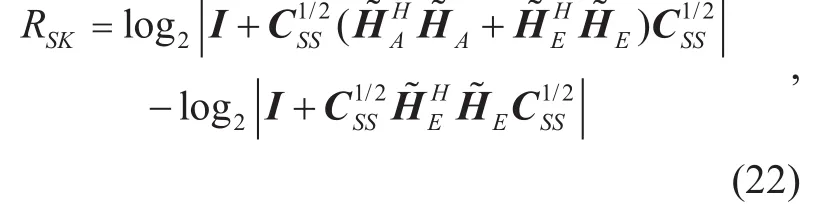
where the last term of (23) is constant quantity. Let pi=, p=(p1,p2,… ,pNA)T, and the sum of the first two terms in (23) is f(p), the SKGR of the optimal power allocation can be written as under the total power constraint

where, E denotes the total transmitting power.Either term in f(p) is convex function about p, but it cannot ensure that f(p) is also convex function. To solve this problem, we do the Taylor series for the second term of f(p).Using first approximation of Taylor expansion for the second term of f(p) at p~, f(p) can be written by

The optimization problems for (25) can be denoted by

VI. SIMULATION RESULTS

To verify the security and suitability of the proposed SKG scheme, we compare the SKGR of the proposed scheme based on private pilot with the approaches using random beam-forming described in [16], which are based on a public pilot, using Monte Carlo simulations. We used the MATLAB information theoretical estimators toolbox developed by Szabo to evaluate the Shannon MI [29].We assume that all the channels are Rayleighfading channels and the entries obey Gaussian distribution with zero mean and unit variance.In addition, we consider the receiver noises as white Gaussian noises with zero mean and unit variance, and Eve can estimate channels HAEand HBEduring the SKG with a public pilot.

Table IV. The optimization SKGR iterative algorithm.

Fig. 2. SKGR varies with the location of attacker.

We first investigate how the location of the MITM attacker Eve affects the SKGR when the transmitting powers of Alice, Bob and Eve are SNR=10 and NA= NE=4, NB=1,2,4 respectively. We normalize the distance from Alice and Bob to Eve as 1, and assume that the channel gain between antenna i of the transmitter and antenna j of the receiver is hj,i=, where dj,iis the distance of the wireless channels from the transmitter to receiver, f～CN(0,1) is a circularly-symmetric complex normal random variable with zero mean and unit variance, and l=2 is the pathloss exponent. We assume that Eve moves along the wireless channels from Alice to Bob,the distance changes from 0.1 to 0.9 in the interval 0.05.

Fig. 2 shows that the SKGRs rise at first,reach the maximum values, and then decrease with the increase of the distance between Alice and Eve, while there are some differences about location of the maximum: it reaches the maximum at 0.6, 0.5 and 0.45, respectively,when NB=1,2,4. It indicates Eve can intercept more information when it is closer to Bob than Alice, and Eve moves to the middle location with the antenna increase of Bob. Since both multi-antenna and high SNR can increase the SKGR, it is consistent with the mathematical theorem that if a +b = c , a ＞0,b ＞0,when and only when a=b=c/2, a×b reaches its maximum.

Secondly, we discuss the effect of the allocated factor of the transmitted power µ on SKGR by the following two scenarios under MITM attacks: 1) NA= 4,NB= NE=1, which applies to MISO scenario to generate secret key; 2) NA= 4,NB= 2,NE=3, which is suitable for MIMO scenario. We assume that the transmitted power of Alice is SNR=10dB, Bob is SNR=1dB, and Eve transmits the received signals as it receives. We mainly explore the SKGR under the three cases: 1) no attacker or eavesdropper; 2) based on public pilot; and 3)based on private pilot.

Fig. 3 presents that the SKGRs based on public pilot decrease with the increasing of m, when m=1, SKGR=0, which is consistent with Theorem 1 that Eve can intercepts all channel information through it. When m=0,the SKGR is equal to the case that there is not attacker or eavesdropper. The initial point of the SKGR based on private pilot is the point that m=0, which is consistent with Theorem 2 that the dynamical private pilot can make the CSI reduce to zero. While the SKGRs based on private pilot first rise, then decrease, and reach the peaks at m=0.5. It demonstrates that SKGR can obtain maximum value when the transmitter averages the transmitting power to each equivalent path. However, if the equivalent channel gains, which do not pass through Eve, are as much as or larger than those passing through Eve, Eve will have to pay great cost to achieve all channel information. Thus we only consider the users that all paths pass through Eve or the equivalent path gains not passing through Eve are very weak. In the following simulations, we assume that the rate of the equivalent channel gains not passing through Eve and passing through Eve is 0.2.

Finally, we investigate the security of the RWC in SQSE by comparing the SKGR based on private pilot and reconstitution channels with that based random beam-forming described in [16] when NA= NE=4, NB=1 and NA= NE= NB=4, respectively, which are corresponding to the MIMO and MISO scenarios, respectively. We explore the SKGR for three cases under the MITM attacks: 1) no attacker or eavesdropper; 2) based on random beam-forming (RBF) described in [16]; and 3)based on the proposed private pilot (PP). The former approaches use public pilot to estimate the wireless channels.

Fig. 4 shows that the SKGRs based on the private pilot and reconstitution channels rise with the increasing of the SNR of the transmitter, which is close to the SKGR without attacker or eavesdropper. However, the SKGR based on random beam-forming with public pilot described in [16] are almost equal to zero under the MITM attacks, which shows that the MITM attack is a serious threat to SKG.

VII. CONCLUSIONS

In this paper, we explore fast SKG based on private pilot under MITM transparent forwarding attacks in static or quasi-static environments. Investigation finds that MITM attacker can intercept all channel state information passing through it when secret key are generated with public pilot using reverse-link channel training. To fight against this attack, we design a dynamic private pilot based SKG scheme.In static or quasi-static environments, we use SVD techniques to reconstitute the wireless channels to improve the randomness of the wireless channels. The results of analysis and simulation show the reconstitution channels have good randomness and the SKGR based on the private pilot and reconstitution channels is close to that without attacker, which can effectively withstand this attack.

Fig. 3. SKGR varies with transmitter’s power allocated factor.

ACKNOWLEDGEMENTS

The authors would like to thank the reviewers for their detailed reviews and constructive comments. The paper was significantly strengthened because of their inputs. This work is supported in part by National Natural Science Foundation of China under Grants No.61601514, 61401510, 61379006 and Project funded by China Postdoctoral Science Foundation: 2016M592990.