Authorized Identity-Based Public Cloud Storage Auditing Scheme with Hierarchical Structure for Large-Scale User Groups

Yue Zhang, Hanlin Zhang, Rong Hao, Jia Yu,3,＊

1 College of Computer Science and Technology, Qingdao University, Qingdao 266071, China

2 State Key Laboratory of Cryptology, Beijing 100878, China

3 State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China

Abstract: Identity-based public cloud storage auditing schemes can check the integrity of cloud data, and reduce the complicated certificate management. In such a scheme, one Private Key Generator (PKG) is employed to authenticate the identity and generate private keys for all users, and one Third Party Auditor(TPA) is employed to by users to check the integrity of cloud data. This approach is undesirable for large-scale users since the PKG and the TPA might not be able to afford the heavy workload. To solve the problem, we give a hierarchical Private Key Generator structure for large-scale user groups, in which a root PKG delegates lower-level PKGs to generate private keys and authenticate identities. Based on the proposed structure, we propose an authorized identity-based public cloud storage auditing scheme, in which the lowest-level PKGs play the role of TPA, and only the authorized lowest-level PKGs can represent users in their domains to check cloud data’s integrity. Furthermore, we give the formal security analysis and experimental results, which show that our proposed scheme is secure and efficient.

Keywords: cloud storage; cloud storage auditing; large-scale users; third party auditor

I. INTRODUCTION

In recent years, more and more individuals and organizations have adopted cloud storage technique, by which users enjoy the enormous storage space in a scalable and economical manner [1]. However, once users store their data in the cloud, they will lose the physical control over their data. As a result, users can not know whether their data stored in the cloud are still intact or not [2]. To solve this problem, a lot of public cloud storage auditing schemes [3-24] are proposed. In these schemes, a Third Party Auditor (TPA) represents users to check the integrity of users’data.

Traditional public cloud storage auditing schemes are based on the public key infrastructure (PKI) system. In such schemes, the public key certificate management is complicated since certificate generation, certificate storage, certificate update and certificate revocation are time-consuming. To optimize the complicated certificate management, recently,some identity-based public cloud storage auditing schemes have been proposed [21-24]. In these schemes, the user’s identity information(such as ID number, e-mail address or name)can be viewed as the public key, and the user’s private key is generated by a trusted PKG.By doing so, the public key certificates are no longer needed, so the workload of certificate management in PKI-based auditing schemes can be reduced.

In this paper, the authors propose an authorized identity-based public cloud storage auditing scheme with a hierarchical structure, which can be applied to the scenario of large-scale users.

In identity-based public cloud storage auditing schemes, the PKG needs to authenticate the identity of each user, and then takes as input the PKG’s master secret key and each user’s identity to generate private keys them.However, when large-scale users request one PKG to generate private keys for themselves,private key generation and identity authentication will cause great computation burden on the PKG [25]. Besides, most of the public cloud storage auditing schemes employ only one TPA to check the integrity of cloud data on behalf of all users. In the real world of large-scale users, it is nearly impossible for one single TPA to complete all auditing work.

To overcome the above issues, we explore how to design an efficient identity-based public cloud storage auditing scheme for largescale users. The contributions of this paper can be summarized as follows:

● We give a hierarchical Private Key Generator structure which can be well applied to large-scale user groups. In this structure,the root PKG delegates private key generation and identity authentication to lower-level PKGs. The root PKG only needs to generate private keys for its domain-level PKGs, and these PKGs generate private keys in turn for the entities in their domains of the next level (the lower PKGs or cloud users). In this way, the workload for PKG is reduced significantly.

● We propose a novel public cloud storage auditing scheme, where the role of TPA is played by the lowest-level PKGs in the hierarchical Private Key Generator structure.In order to make our scheme more secure and robust, we design auditing authorization to eliminate threats of unauthorized audit challenges from malicious or pretended TPA. In our scheme, the lowest-level PKGs will get auditing authorizations from the users in their domains, which ensures that only the corresponding lowest-level PKG can perform auditing work for users in its domain. We give correctness analysis, security analysis and performance evaluation.

II. RELATED WORK

In order to realize the remote cloud data integrity checking, Ateniese et al. [3] firstly proposed “Provable Data Possession” (PDP),which utilized strategies of homomorphic authenticators and sampling. Utilizing spot checking and error-correcting codes strategies,Juels et al. [4] proposed a “Proof of Retrievability” (PoR) model. The “Proof of Retrievability” (PoR) model can not only ensures the possession of cloud data, but also can proof the retrievability of cloud data. Based on BLS signature, Shacham et al. [5] constructed a compact PoR scheme. To relieve the burden on cloud users for cloud data integrity auditing,Wang et al. [6] introduced a Third Party Auditor (TPA) who can represent users to verify the integrity of cloud data. When TPA challenges the same data blocks multiple times during the data auditing, he/she might derive the contents of user’s data. To deal with this problem, by utilizing random masking technique, Wang et al. [7,8] constructed privacy-preserving public cloud storage auditing schemes. In addition,key exposure is a practical problem in cloud storage auditing. Yu et al. [12,13,14] proposed some cloud storage auditing schemes with key-exposure resilience, which reduced the damage of key exposure in cloud storage auditing. To avoid the DDoS attacks from malicious or pretended TPAs, Liu et al. [16]proposed a cloud storage auditing scheme with DDoS attacks resilience, which added an auditing authentication process between the auditor and the cloud. In practice, users might store their data in the cloud and share them with other users. Therefore, supporting cloud storage auditing for shared data is also very important. Recently, several public cloud storage auditing schemes for shared data [17-20]have been proposed. However, most of above cloud storage auditing schemes are designed in the Public Key Infrastructure (PKI) system.There exists complicated certificate management in these schemes, such as certificates generation, delivery, revocation, renewal and so on.

In recent years, some identity-based public cloud storage auditing schemes have been proposed to simplify the public key certificate management. Wang et al. proposed the first identity-based public cloud auditing scheme [21], in which the user’s identity(such as ID number, e-mail address or name)can be viewed as the public key, and the user’s private key was generated by a trusted PKG. After that, Yu et al. [22] proposed an identity-based remote data integrity checking scheme with perfect data privacy-preserving, which achieved zero-knowledge privacy against the verifier. Wang et al. [23] proposed an incentive and unconditionally anonymous Identity-based public cloud storage auditing scheme, which protected the identity privacy of users and allowed users to disclose the bad event. Wang et al. [24] proposed an identity-based distributed provable data possession scheme, which was in multiple-cloud storage and cloud user’s authorization. However, all existing identity-based public cloud storage auditing schemes only support one PKG.When the user scale is large, the capability of the PKG might become a bottleneck. How to design a secure and practical identity-based public cloud storage auditing scheme for large-scale users is a critical unexplored problem.

III. HIERARCHICAL PRIVATE KEY GENERATOR STRUCTURE AND AUDITING MODEL

3.1 Hierarchical private key generator structure

As illustrated in figure1, the hierarchical Private Key Generator (PKG) structure in this paper includes three different kinds of entities: the root PKG, lower-level PKGs and users.

The above entities form a hierarchical tree, in which the root PKG is at the top, the users are at the bottom, and the lower-level PKGs are the nodes between them. To identify an entity in the hierarchical tree, we use an ID-tuple (I D0,I D1,I D2,...,I Dt) as the identity information. The ID tuple denotes the route from the root PKG ID0to the entity IDt. In this way, each entity’s identity is unique. For convenience, we use PKG0to represent the root PKG, PKGjto represent a lower-level PKG at level j (where 1 ≤j≤t-1 and t≥2), and Utto represent a user at the bottom level. For a user Utwith ID-tuple(I D0,I D1,I D2,...,I Dt), we denote the entity with ID tuple (I D0,I D1,I D2,...,I Dt-1) as Ut’s parent, and denote entities with ID tuple(I D0,I D1,I D2,...,I Dj) (where 0 ≤j≤t-1) as Ut’s ancestors at level j.

3.2 Auditing model

As illustrated in figure 2, the auditing model of our scheme includes three different kinds of entities: user, cloud and PKGt-1.

● User: The entity Utwith ID tuple(I D0,I D1,I D2,...,I Dt) who is at the bottom level in the hierarchical PKG structure. The user has a large number of data files to be stored in the cloud.

Fig. 1. The hierarchical Private Key Generator (PKG) structure.

● Cloud: The entity who has enormous storage space and powerful computation resource to process the user’s data.

● PKGt-1: The entity who is user Ut’s parent in the hierarchical PKG structure. The PKGt-1plays two important roles: 1) generates private keys for user Ut; 2) plays the role of TPA, checking the integrity of cloud data on behalf of user Ut. When the PKGt-1checks the integrity of cloud data,he will send his auditing authorization and an auditing challenge to the cloud. After that, the cloud will verify the validity of the authorization, and respond to PKGt-1with a data possession proof. Finally, the PKGt-1checks the correctness of the proof, and then it can judge whether the cloud data is intact or not.

IV. DEFINITION AND PRELIMINARIES

4.1 Definition of the scheme

An authorized identity-based public cloud storage auditing scheme with hierarchical structure for large-scale users includes the following seven algorithms:

1) Root Setup(1k): This algorithm is run by PKG0. It takes as input the security parameter k. It outputs the root secret key x0and system public parameters params.

2) Lower-l evel- setup(p arams ): This algorithm is run by lower-level PKGs. Each lower-level PKG generates a secret key xt,and computes the corresponding verification value Yt.

Fig. 2. The authorized auditing model.

3) Extract(p arams, (σt-1,Rt-1),I D): This algorithm is run by an entity’s parent PKGt-1to generate the private key for the entity(the entity might be the lower-level PKG or the cloud user). It takes as input the system public parameters params, the PKGt-1’s private key (σt-1,Rt-1), and the ID-tuple of the entity. It outputs the private key (σt,Rt)of the entity.

4) AuthGen(ID): This algorithm is run by a cloud user with ID tuple(I D0,I D1,I D2,...,I Dt) to generate an auditing authorization for his/her parent PKGt-1.It takes as input the user’s ID tuple. It outputs an auditing authorization Auth for the parent PKGt-1.

5) TagGen (σt,F = (m1,...,mn)): This algorithm is run by a cloud user with ID tuple(I D0,I D1,I D2,...,I Dt) to generate signatures for his/her data. It takes as input the private key σtand a file F, where the file F is an ordered collection of data blocks {mi}i∈[1,n].It outputs the set of signatures ∑, which is an ordered collection of {Ti}i∈[1,n]on data blocks {mi}i∈[1,n].

6) Gen Pro of(F ,Σ,c hal,A uth): This algorithm is run by the cloud to generate the integrity proof. Firstly, the cloud verifies the correctness of the auditing authorization received from the TPA. If the auditing authorization is invalid, aborts; otherwise, the cloud takes as input the file F, its signatures set ∑ and the auditing challenge chal, and outputs an auditing proof P that is used to demonstrate that the cloud truly possesses this file.

7) Verify(p arams,I D,P,c hal): This algorithm is run by the TPA to verify the correctness of proof provided by the cloud. It takes as input the system public parameters params,the auditing challenge chal, the ID-tuple of the user and the auditing proof P. It outputs‘success’ or ‘failure’, representing whether the proof P is correct or not.

4.2 Preliminaries

4.2.1 Bilinear maps

Let G1and G2be two cyclic multiplicative groups, which are with the same prime order q, that is,

be a bilinear map, which satisfies that [26]:

● Bilinearity: For all g1,g2,g3∈G1and a,b∈

● Non-degeneracy: e(g4,g5)≠ 1, where g4,g5∈G1.

● Computability: there exists an efficient algorithm to calculate e(g6,g7), where g6,g7∈G1.

4.2.2 Computational diffie-hellman (CDH)assumption

Let G1be a cyclic multiplicative group of prime order q. The CDH assumption states that, given g,gxand gy∈G1, where x,y∈Zq∗,it is computationally intractable to compute the value gxy∈G1.

4.2.3 Discrete logarithm (DL) assumption

Let G1be a cyclic multiplicative group of prime order q. The DL assumption states that,given g,gx∈G1, where x∈Zq∗, it is computationally intractable to compute the value x.

V. THE PROPOSED AUDITING SCHEME

1) Root Setup(1k): A file F that will be uploaded is split into n blocks (m1,...,mn), where midenotes the i-th block of F and mi∈ Zq*.The root PKG (PKG0) chooses two multiplicative cyclic groups G1and G2with the prime order q＞2k, and a bilinear map e:G1× G1→G2. Let g and u be two generators of G1. PKG0selects two cryptographic hash functions: H :{0,1}*× G1→Zq*and h :{0,1}*→ G1. Also PKG0randomly chooses x0∈as the root secret key,and computes Y0= gx0. PKG0publishes(G1,G2,e,q,g,u,Y0,H,h ) as the system public parameters params.

2) Lower-l evel- setup(p arams): Each PKGtat level t(t≥1) randomly picks xt∈ Zq*as a secret key, and sets Yt= gxt∈G1as the verification value.

3) Extract( params, (σt-1,Rt-1),I D): Let Etbe an entity (the lower-level PKG or the cloud user) at level t(t≥1) with ID tuple(I D0,I D1,I D2,...,I Dt). Et’s parent generates the private key for Etas follows:

i. Picks rtrandomly, and computes

ii. Computes σt= σt-1+ rt+xt-1H(I D0||ID1||I D2||...||I Dt,Rt)mod q, where σt-1is the private key of Et’s parent. Here, for consistency, we define σ0=0.

iii. Sends (σt,Rt) to Etas the private key.

iv. Also sends Rj(1≤ j ＜t ) and Yj(0≤ j ＜t) to Etfor verifying the correctness of the proof from the cloud.

4) AuthGen(ID): A user Utwith ID tuple(I D0,I D1,I D2,...,I Dt) generates an auditing authorization for the TPA (his/her parent PKGt-1): The user randomly picks x∈as the secret key for authorization generation, and computes V=gxas the authorization verification value.Then computes the auditing authorization Auth =(h(I D0||I D1||I D2||...||I Dt))x. The user sends the auditing authorization Auth to the TPA, and sends V to the cloud.

5) TagGen (σt, F = (m1,...,mn)): The user Utwith ID tuple (I D0,I D1,I D2,...,I Dt) generates a signature for each block miof the file F. This algorithm is described as follows:

i. The user computes Ti=where i is the index of the block mi. ∑={Ti}1≤i≤nis the set of signatures.

ii. The user uploads the set of signatures Σ and file F to the cloud.

6) Gen Pro of(F ,Σ,c hal,A uth):

i. The TPA will generate an auditing challenge when it audits the integrity of cloud data:

a) The TPA picks a set of elements randomly,in which I⊆[1,n].

b) The TPA generates a random value v ∈ Z∗

i q for each i∈I.

c) The auditing challenge chal={i,vi}i∈I, the TPA sends the challenge and auditing authorization Auth to the cloud.

ii. Then the cloud verifies the correctness of the challenge and the auditing authorization: The cloud verifies the correctness of auditing authorization by checking whether the equation e(A uth,g ) = e(h(I D0||I D1||I D2||...||I Dt),V )holds. If the auditing authorization is valid,then the TPA is legitimate. The cloud computesand sends P=(T,) to the TPA as the proof of data possession.

7) Verify(p arams,I D,P,c hal ): After receiving the proof P=(T,mˆ) from the cloud, the TPA verifies the correctness of the proof by checking whether the following equation holds:

If the above equation holds, then the proof is correct and the TPA outputs ‘success’; otherwise, the TPA outputs ‘failure’.

VI. CORRECTNESS AND SECURITY ANALYSIS

In this section, we analyze the correctness and the security of the proposed scheme.

Theorem 1. If the cloud, the user Utand the TPA (Ut’s parent PKGt-1) are sincere and obey the specified procedures, then the response proof can pass the TPA’s checking.

Proof: From the characters of bilinear maps, the verification equation can be deduced from the left-hand side to the right-hand side shown in (2) at the bottom of this page.

Theorem 2: Only the TPA who gets valid auditing authorization can receive the auditing proof from the cloud.

Proof: The auditing authorization Auth is constructed based on BLS signature in our scheme. According to the unforgeability of BLS signature, other parties except the authorized TPA cannot forge a valid auditing authorization. The malicious auditors cannot pass cloud’s verification when they send auditing challenges to the cloud. Thus, only the TPA authorized by Utcan receive the auditing proof reply from the cloud.

Theorem 3: In our proposed scheme, the cloud can pass the TPA’s verification only when the cloud truly stores users’ intact data.

Proof: We will prove that, if a malicious cloud forges an auditing proof on corrupted cloud data and wins the following security game, then we can solve the Discrete Logarithm (DL) problem in G1. Security game is described as follows:

Security game: When TPA sends an auditing challenge {i,vi}i∈Ito the cloud, the audit-ing proof on correct cloud data F is P=(T,mˆ).However, the cloud wants to generate proof on incorrect data F′, and the invalid proof P=(T,). Define). If this invalid proof can pass the TPA’s verification successfully, we think the malicious cloud wins the game; otherwise, it fails the game.

We assume the malicious cloud wins the above game. Then we have the following equation by equation (1):

From the above two equations, and apply the characters of bilinear maps, then we get

Furthermore, we can deduce that

Given (g,h)∈G1, because G1is a cyclic group, so there exists x∈Zq*and h=gx. Without loss of generality, given g,h, and set u = gahb∈ G1, in which a and b are two random elements of Zq∗. As a result, we find a way to solve the Discrete Logarithm (DL) problem in G1, that is,Then the solution for the DL problem is,

Note that b is zero only with the probability 1/q. Because q is a large prime, so we think the probability of b is zero is negligible. Furthermore, we can solve the DL problem with the probability 1-1/q. However we assume the DL problem in G1is hard. It contradicts our assumption. Therefore, it is computationally infeasible for a malicious cloud to generate a forged auditing proof on corrupted cloud data.

VII. PERFORMANCE EVALUATION

7.1 Performance analysis

We use the following notations to denote different operations in our scheme: Mul is one multiplication operation in G1; Exp is one exponentiation operation in G1; MulZq*is one multiplication operation inAddZq*is one addition operation inHashG1is one hash operation in G1;is one hash operation inPair is one pairing operation;p is the size of an element in group G1;q is the size of an element inWe analyze the overhead of computation and communication in Extract phase, Authorization phase and Auditing phase since they are the most resource-consuming phases in our scheme:

7.1.1 In the Extract phase:

● The computation overhead: The computation overhead that the parent PKGt-1of an entity Etcomputes the private key σtfor him/her is Exp + Mul + 2

● The communication overhead: The transmission of private key σt, Rj(1≤ j ＜t) and Yj(0≤ j ＜t) between the parent PKGt-1and the entity Etcosts (2t-1)bits.

7.1.2 In the Authorization phase:

● The computation overhead: The computation overhead of auditing authorization generation is HashG1+2 Exp. After receiving the authorization, the cloud will verify the correctness of the auditing authorization, which costs HashG1+2 Pair .The total computation overhead is 2 HashG1+ 2 Pair + 2Exp.

● The communication overhead: The transmission of auditing authorization message Auth and the authorization verification value V between thre user and his/her parent PKGt-1both costp bits. The total communication overhead is2p bits.

7.1.3 In the auditing phase:

● The computation overhead: The computation overhead of proof generation is(c - 1)M ul+ cExp + (c - 1)+.After receiving the proof, the TPA will verify the correctness of the proof, which costs+ (c + 2t - 1)M ul + (c +t+1)Exp+2Pair. The total computation overhead is cMulZq*+ cHashG1+ tHashZq*+ (2c + 2t - 2)Mul +(2 c + t + 1)E xp + 2 Pair + (c - 1)AddZq*.

● The communication overhead: The size of an auditing challenge Chal={i,vi}i∈Iis cbits, wheredenotes the size of a block index; the size of an auditing proof P=(T,) isbits.The total communication overhead is(c +1)bits.

7.2 Experimental results

Fig. 3. Comparison of the computation overhead of private key generation for different number of users between our scheme and scheme [21].

Fig. 4. Comparison of the computation overhead of challenge generation between our scheme and scheme [21].

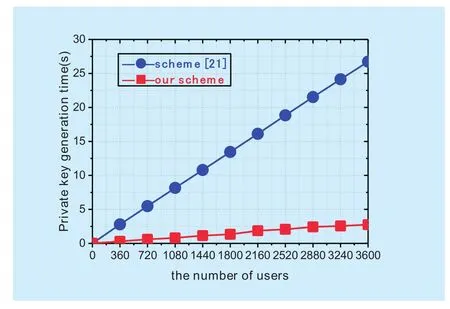
Fig. 5. Comparison of the computation overhead of proof verification between our scheme and scheme [21].

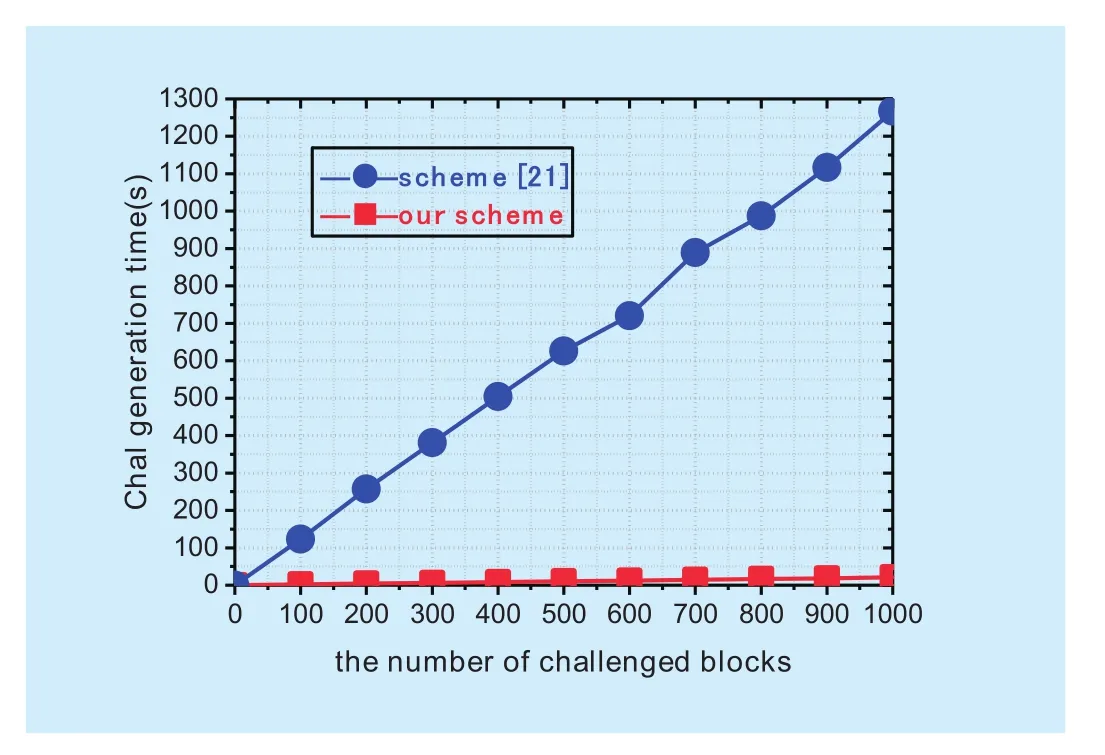
Fig. 6. The computation overhead of proof generation in our scheme.

To show the efficiency of our scheme, we simulate our scheme in this subsection. We assume the hierarchical tree has two levels, and each internal node has 60 children. The total number of users at the bottom level is 3600.Each user has a file to be stored in the cloud.The size of each file is 20MB, which consists of 1,000,000 blocks. Our experiments are based on the free Pairing-Based Cryptography(PBC) Library and the GNU Multiple Precision Arithmetic (GMP) Library. We conduct these experiments on Linux OS with an Intel Pentium running at 2.70GHz processor and 4GB memory. In these experiments, the size of base field is set to be 512 bits, the size of an element in Zq*is set to be 160 bits.

Performance in the Extract phase: To evaluate the performance of private key generation in our scheme and scheme [21], we choose to generate private keys for different number of users from 0 to 3600 increased by an interval of 360. As shown in figure 3, the computation overhead of private key generation in scheme [21] ranges from 2.78518s to 26.73724s. The overhead in our scheme is very small. It ranges from 0.29952s to 2.75076s. Therefore, we conclude that our scheme achieves more efficient private key generation for large-scale user group compared with scheme [21].

Performance in the Auditing phase: In the auditing phase, the TPA is in charge of challenge generation and proof verification,the cloud is in charge of proof generation. To show the efficiency of TPA in our scheme,we compare the overhead of proof generation and proof verification in our scheme against scheme [21]. In this experiment, the TPA performs challenge generation and proof verification for 3600 users. The number of challenged blocks ranges from 100 to 1000. As shown in figure 4 and figure 5, the overhead of TPA in our scheme is much smaller compared with scheme [21]. In order to show the performance of cloud in our scheme, we evaluate the overhead of cloud for proof generation. From figure 6, we can see that with more number of blocks being challenged, the proof generation costs longer time.

VIII. CONCLUSION

In this paper, we propose an authorized identity-based public cloud storage auditing scheme with a hierarchical structure, which can be well applied to the scenario of large-scale users. In our scheme, we give a hierarchical PKG structure, in which the root PKG delegates lower-level PKGs to generate private keys and authenticate identities. Based on this structure, we propose a novel cloud storage auditing scheme, in which only the authorized lowest-level PKGs can represent users in their corresponding domains to check the integrity of cloud data.

ACKNOWLEDGEMENTS

This research is supported by National Natural Science Foundation of China (No. 61572267,No. 61272425, No. 61402245), the Open Project of Co-Innovation Center for Information Supply & Assurance Technology, Anhui University, the Open Project of the State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences(No. 2017-MS-21, No. 2016-MS-23),National Cryptography Development Fund of China (MMJJ20170118).