某水电站溢洪道开挖边坡渗流场变化规律及稳定性研究

黄叶宁 孙旭曙 迟 健 刘 洋 陈 超 梁佳灯

(三峡大学 水利与环境学院， 湖北 宜昌 443002)

水利水电工程建设形成的边坡所处工程环境复杂，且长期处于库水位循环升降作用下，对边坡岩土体物理力学参数都有一定程度的劣化影响，从而对其稳定性产生影响．边坡失稳造成的滑坡、崩塌是十分严重的自然灾害，其危害仅次于第2大地质灾害的地震[1]．边坡开挖改变了天然边坡的几何形状，对边坡渗流场产生一定影响从而影响其稳定性．因此，对库水位升降过程中的开挖边坡渗流场和稳定性问题需持续研究．

文献[2-5]以实际边坡工程为例，根据Geo Studio软件的SEEP/W与SLOPE/W模块对瞬态渗流条件下的边坡进行稳定性分析，得出了库水位升降对边坡渗流场和稳定性影响的一般规律．文献[6-8]通过试验获取边坡岩土体的力学参数，测量库水升降过程中滑坡体内土压力、孔隙水压力的变化情况，从而分析水库蓄水和下降过程中边坡的变形破坏特征．上述文献已对库水作用下边坡内部地下水位变化及其对稳定性的影响进行了深入研究，但边坡开挖之后，其原始地貌将发生变化，就有限元计算模型而言，首先其几何模型发生变化，导致边坡荷载发生变化；其次渗流边界条件发生变化，从而影响渗流场．上述因素都将影响边坡的稳定性．因此，掌握边坡开挖后渗流场及其稳定性的变化规律具有重要的工程意义．

本文基于饱和-非饱和渗流理论和刚体极限平衡法，采用数值模拟方法研究库水升降作用下边坡开挖前后渗流场变化规律及其对边坡稳定性的影响．

1 计算理论及方法

1.1 渗流计算

Geostudio系统软件中的SEEP/W模块的理论公式基于饱和与非饱和土体渗流的达西定律[9]，表述如下：

v=ki(1)

式中，v为达西流速；k为渗透系数；i为总水头梯度．

SEEP/W模块中瞬态二维渗流的一般控制微分方程可表述为[10]：

(2)

式中，H为总水头；kx为x方向的渗透系数；ky为y方向的渗透系数；Q为施加的边界流量；t为时间；mw为出水曲线的斜率；γw为水的容重．

1.2 稳定性计算

本次计算采用Morgenstern-Price法进行稳定性分析，该方法考虑了条间剪力和法向力并同时满足弯矩平衡和力的平衡．Morgenstern-Price法[10]根据弯矩和水平力平衡条件，通过FOS迭代计算滑动面的安全系数．

弯矩平衡的安全系数可表述为：

(3)

水平方向静力平衡的安全系数可表述为：

(4)

式中，c′为有效粘聚力；φ′为有效摩擦力；u为孔隙水压力；N为土条底部法向力；W为土条重量；D为集中荷载；β，R，x，f，d，ω为几何参数；α为土条底面倾角．

中药汤剂联合丙酸氟替卡松治疗变应性鼻炎患者对其血清Th1/Th2细胞因子及VCAM-1水平的影响（唐爱华）3∶190

1.3 计算方法

本次数值分析包括边坡饱和-非饱和渗流计算和稳定分析两部分内容．首先，采用GeoStudio软件中的SEEP/W模块分析库水位升降过程中坡体内部水头分布和浸润线的变化规律；其次，在此基础上分析库水位升降作用对边坡稳定性的影响．

2 工程实例

2.1 工程概况

某水电站处于西藏自治区芒康县境内，溢洪道布置于河流左岸，且距大坝左坝肩约50 m，溢洪道边坡自然坡度为40°～50°，出露地层岩性为三叠系中统竹卡组(T2z)英安岩、流纹岩，大多基岩祼露，岩体风化强烈，并发育多个碎裂岩体，岩体一般呈强～弱风化、山脊一带岩体局部呈全风化状态，承载力和变形模量大部分基本满足要求．坝址河段枯期河水位2 615.6 m，水库正常蓄水位2 895 m，死水位2 825 m．

2.2 计算模型及参数

根据该工程溢洪道典型地质剖面图，岩层可分为碎裂岩体、全风化、强风化、弱风化上带、弱风化下带、微分化和微新岩体，有限元计算模型如图1所示．

图1 溢洪道边坡计算模型

参考地质勘查报告、文献[11]和GEO-SLOPE软件自带数据库确定岩土体物理力学参数，其参数见表1．

2.3 计算工况

本次计算考虑了库水位升降速率和边坡岩土体渗透系数对溢洪道边坡渗流场和稳定性的影响，按表2中的工况模拟计算．有限元模型中，坡体左、右两侧地下水位、正常蓄水位和死水位均为定水头边界条件，当考虑库水位上升和下降时，库水位为随时间变化的函数．

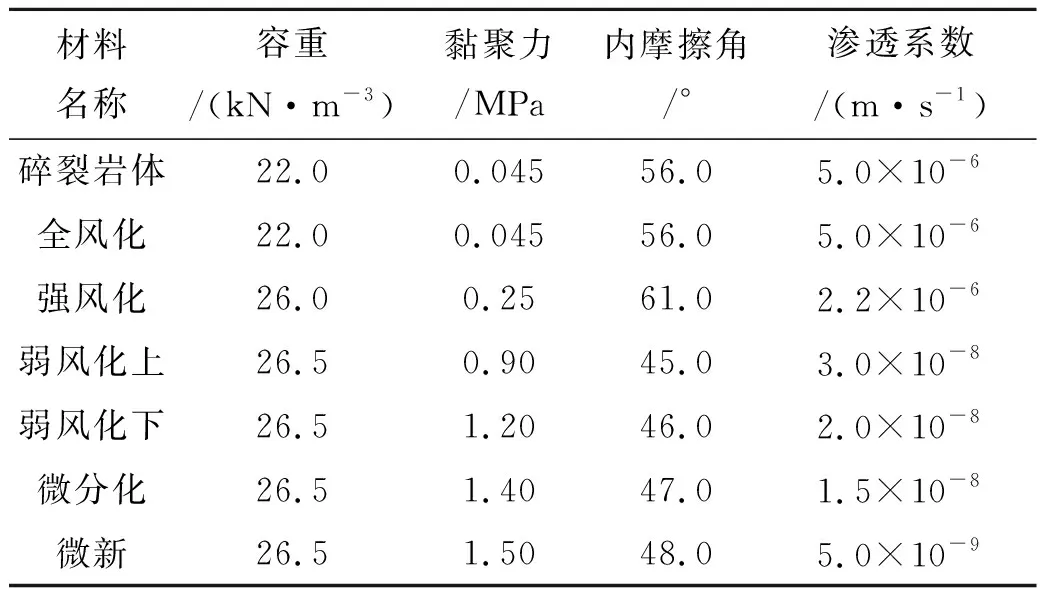
表1 溢洪道边坡岩土体力学参数表

表2 计算工况

3 计算结果分析

3.1 渗流计算分析

1)工况1

边坡开挖前后坡体内部浸润线分布如图2所示．结果表明：在原地下水面线以上开挖边坡，不会对浸润线分布产生影响．

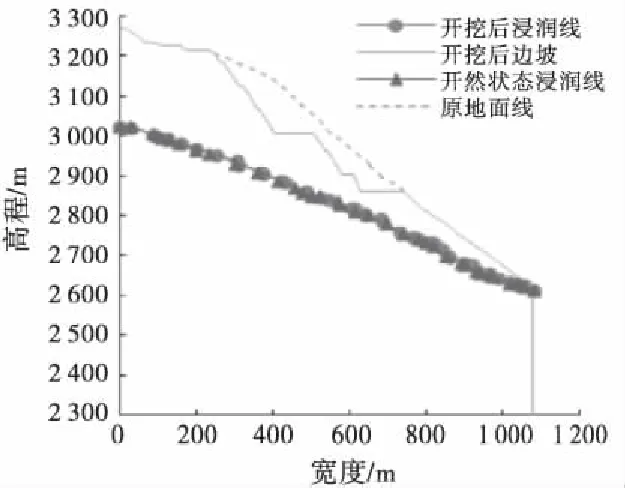
图2 枯水期边坡开挖前后地下水位分布

为分析库水位升降过程对坡体内部渗流场变化规律的影响，从左至右选取11个监测点，各点位置如图3所示．以1 m/d的升降速率为例分析库水升降过程对边坡渗流场的影响，库水上升、下降过程中各点总水头变化曲线如图4所示．结果表明：对比库水位上升和下降过程，横坐标0～400 m处地下水位几乎无变化，400～1 080 m处浸润面随着库水位升降而变化，表明边坡浅层局部区域及受库水位直接影响区域的渗流场受库水位升降作用更为敏感．

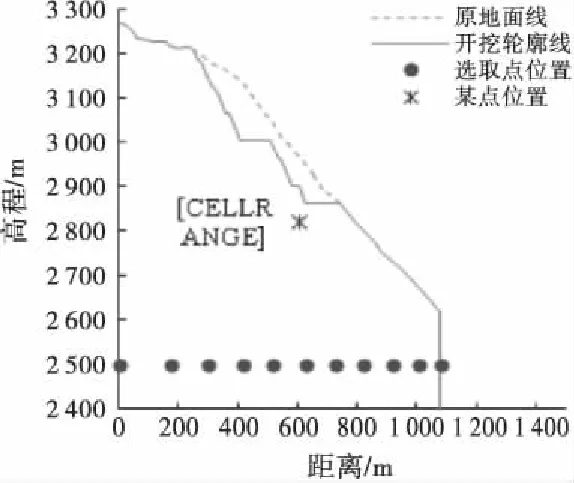
图3 选取各点位置示意图

图4 开挖后各点总水头随距离变化曲线

选取坡体开挖平台下部P12点(如图3所示)，分析不同库水位升降速率0.5 m/d、1 m/d、2 m/d对边坡渗流场的影响，3种升降速率下P12点总水头随时间的变化曲线如图5所示．

图5 不同升降速率某点总水头随时间变化曲线

结果表明，①库水位以不同速率上升时，P12点处总水头总体变化趋势为缓慢增加→快速上升→趋于稳定，库水位上升速率越大，曲线上升段起始时间越早，曲线斜率越大；当库水位上升速率为0.5 m/d时，在计算时间内无稳定段；②库水位以不同速率下降时，P12点处总水头总体变化趋势为快速下降→缓慢下降，库水位下降速率越大，曲线斜率变化越剧烈．分析原因，库水升降速率越快，坡体内外形成的水头差越大，导致坡体内外水力坡降加大，渗流速度加大，渗流场孔压变化加快．

3)工况3

此工况库水位升降速度设为1 m/d，坡体材料的渗透系数分别设为K×10、K、K×10-1．选取坡体靠近下游侧的P12，可得3种渗透系数下该点总水头随时间的变化曲线如图6所示．结果表明，库水位上升时，P12点总水头先缓慢增加再快速增加，库水位下降时，P12点总水头先快速下降再缓慢下降；且渗透系数越大总水头变化速率越快．

图6 不同渗透系数某点总水头随时间变化曲线

3.2 稳定性计算分析

1)工况2

不同库水位上升速率条件下，溢洪道边坡安全系数随时间变化曲线如图7所示．结果表明：①当库水位上升时，3种速率对应的安全系数总体变化趋势为相对稳定→快速降低→趋近稳定；库水位上升速率大时，坡体安全系数快速下降起始时间越早，且在较短时间内趋于稳定；库水位上升速率最小时，在计算时间内无稳定段．②库水位下降时，安全系数总体呈现出快速下降→缓慢下降→趋于稳定的变化趋势；库水位下降速率越快，安全系数下降越快．

图7 不同升降速率安全系数随时间变化曲线

2)工况3

不同渗透系数条件下，库水位按1 m/d速率升降考虑，溢洪道边坡安全系数随时间变化曲线如图8所示．

图8 不同渗透系数安全系数随时间变化曲线

结果表明：①库水位上升时，3种渗透系数对应的安全系数总体趋势为相对稳定→快速降低→趋于稳定；坡体渗透系数增大时，安全系数下降的幅度增大，在计算时段内无稳定段．②库水位下降时，坡体的安全系数大致呈下降趋势，最后趋于稳定，且渗透系数大时，安全系数下降的幅度也大，曲线最陡．

4 结 论

1)在原地下水面线以上开挖边坡，不会对地下水位线分布产生影响．2)总体来说，坡体内地下水位线随着库水位升降而升降，但坡体浅层对库水位升降的变化更敏感．3)库水位上升过程中，坡体安全系数呈现保持不变→快速降低→趋于稳定的变化趋势，且上升速率越快，安全系数降低的速率越快；库水位下降过程中，坡体安全系数随水位的下降而降低最后趋于稳定，且下降速率越快，安全系数降低的速率越快．