数学之美之数形结合
2018-11-23蔡萃艺
蔡萃艺
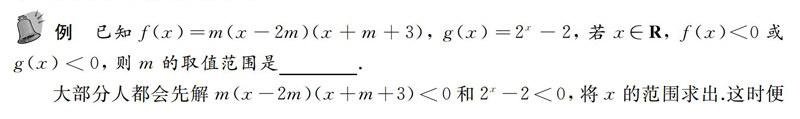
依稀记得刚走进初中大门之时,数学老师在班级公共邮箱里放了一份《数学之美》的ppt文件.点开后,是一张张精美的几何动态图,几张体现数与数之间运算规律的宏大的平面图,数与形的美妙结合给我带来了强烈的视觉冲击.曾经的我单纯地认为数学就是数字的运算,只有通过缜密的头脑风暴才能将数学运用得如鱼得水,而数字就是人们操控数学的秘密武器,在我将那份ppt从头到尾一图不落一字不漏地看完后,之前在脑海中构建出的数学概念堡垒,瞬间被一个个奇形怪状的立体图形轰炸成碎片,需要被替换、更新、重组.
虽说有被数学之美惊艳到,但内心其实还充满着对数学学习的恐惧,人们总是对未知的事物有着探索的渴望;与渴望并存的,还有对探索结果的恐惧.一想到这些“美”的背后烦琐的证明过程,复杂的计算方法,我总是踟蹰在数学之美的表面,难以感受到它背后更具有深度的美.这就仿佛给数学蒙上了一层朦胧的面纱,你深知面纱之下的真容能够触动大脑里最僵硬的那根神经,给你一种如释重负、恍然大悟的快感,但却捉摸不透揭开那层面纱的方法,
总而言之,数学不单单研究数字,它还研究结构、变化、空间以及信息等方面,从某种角度看属于形式科学的一种.
在小学数学的学习中,几何与数字的关系并不是非常紧密,稍有涉及的无非是计算图形的面积、周长,要求稍微高点则是计算最值问题等.到了初中,图形的种类变得丰富起来,函数也登上了数学的舞台,这两者之间的结合便构成高中试卷压轴题型——考查数形结合的函数题.
函数可以用图象来表示,其中必然会涉及几何问题;几何图形里大有文章可做,最为宠幸的便是函数.这两者的结合可谓是“双剑合璧”了.华罗庚曾说过:“数形结合百般好,隔离分家万事休”,“数”与“形”反映了事物两个方面的属性,而数形结合,主要指的是数与形之间的一一对应关系.
运用数形结合的思想解题可以起到事半功倍的成效,在过去接触的大部分题目里,题干中并不会给出明确的提示来揭示这道题的本质是数形结合的应用,这就要求我们做题时拥有一种敏锐的直觉.原式进行各种变形转化后还是无法找到解题的突破口,就可以换一种思路,采用数形结合的方法来解决,
例 已知f(x)=m(x-2m)(x+m +3), g(x) =2x-2,若x∈R,f(x)<0或g(x)<0,则m的取值范围是____.
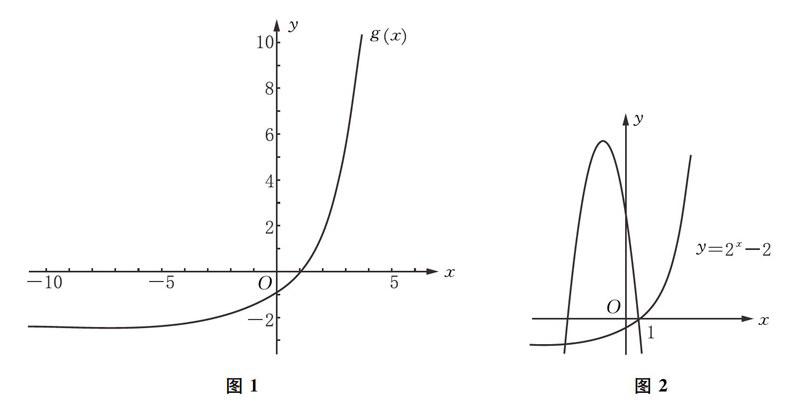
大部分人都会先解m(x-2m)(x+m+3)<0和2x-2<0,将x的范围求出,这时便需要注意条件中的“或”字,说明两者中只需有一者小于零即可,但由于m的正负未知,2m与m 3的大小也就无法确定.进行分类讨论的工作量可以说是十分大了.不妨换条路走,f(x)是二次函数形式,可以画出它大致的图象,g(x)的图象是可以确定的,于是我们可以得到图1.
由图可知,当x<1时,g(x)<0,因此此时f(x)的图象只要是抛物线即可.当x≥1时,因为g(x)>0,所以f(x)<0,这时就要求我们对x≥1时f(x)的图象进行条件限制.首先先确定m的正负,由它来决定f(x)图象的开口方向.当m>0时,图象开口向上,则x趋于正无穷时总会有f(x)>0恒成立,因此m必须为负数,所以f(x图象与x轴的交点为(2m,0)和(-m-3,0),就如图2.再通过确定交点的左右位置即可对m进行分类讨论,求解就简单多了.
由此可见,数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数助形”,即通过抽象思维与形象思维的结合,使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的,这个方法常常与以下内容有关:实数与数轴上的點的对应关系,函数与图象的对应关系,曲线与方程的对应关系,以几何元素和几何条件为背景建立起来的概念(如三角函数)等,
我们要在平常做题的过程中,不断总结积累,慢慢领悟出数形结合的思想方法,让两者相得益彰地辅助我们思考,从而达到解决问题的目的,如果说代数与几何是数学界的两大强者,强强针锋相对之时你不知所措,只会被夹在中间受到二倍技能的伤害,倘若你选择避开,同样会造成两败俱伤,而你则无利可收.因此不如试着将它们征服于股掌之间,融合出更为强大的必杀技,想必到那时,许多囤积的难题便可以迎刃而解了.
点评 数形结合是高中数学学习中一个非常有效的方法,该生能感受到其中的生动有趣,体会到数学之美,对其将来的数学学习必有助益.
