线性回归与逻辑回归的比较分析

(广东邮电职业技术学院 广东 广州 510630)

一、引言

最简单的回归可以追溯到一元一次方程式，形如y=ax+b这就是回归的最基本形式，当a，b已知的情况下，我们可以根据x的值代入方程式中得到y的值。显而易见，这是一种非常简单的数学运算，但是现实情况中，参数a，b是不知道的。例如：假设一个便利店，每天的顾客人数和该商店的营业额存在这样的线性关系，那么我们可以统计n天内，每天该商店的人数x和营业额y。通过统计的样本可以很容易得到回归方程式。这是一种理想状态下的假设，影响营业额的因素往往有很多，比如顾客的平均年龄，顾客的性别比例等。所以真实的线性回归不仅仅是一个变量x，而是多元的。这里的x称之为特征。

二、回归模型

(一)线性回归

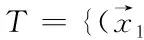
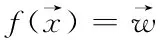
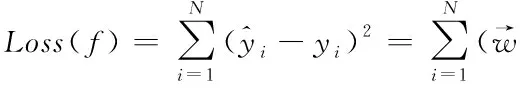
目标函数也就是损失函数最小化：

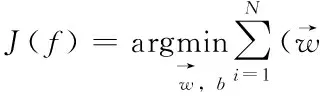
(二)逻辑回归

逻辑回归又称Logistic Gression。对线性回归主要是用来预测标签是连续的场景。然而人们发现回归也可以运用于分类场景。比如二分类、给定数据集T。

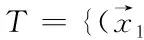
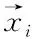
我们需要知道P(yi/xi)。显然逻辑回归的目标是预测x发生条件下。由于线性回归方程得到值是连续的，所以在对分类的处理上需要将值映射到{0,1}的状态上来。

于是引入了Logistic函数：

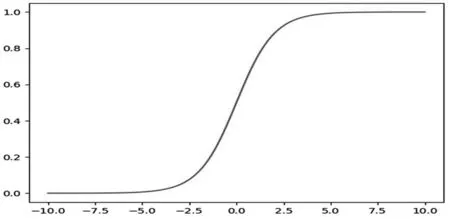
图1 逻辑回归的阶跃函数

整合以上方程，可以得到回归模型：

三、实验

(一)线性回归实验

主要选取波士顿房价数据特征是一维的，主要是房间数量，针对数据集训练得到线性回归模型预测房价。

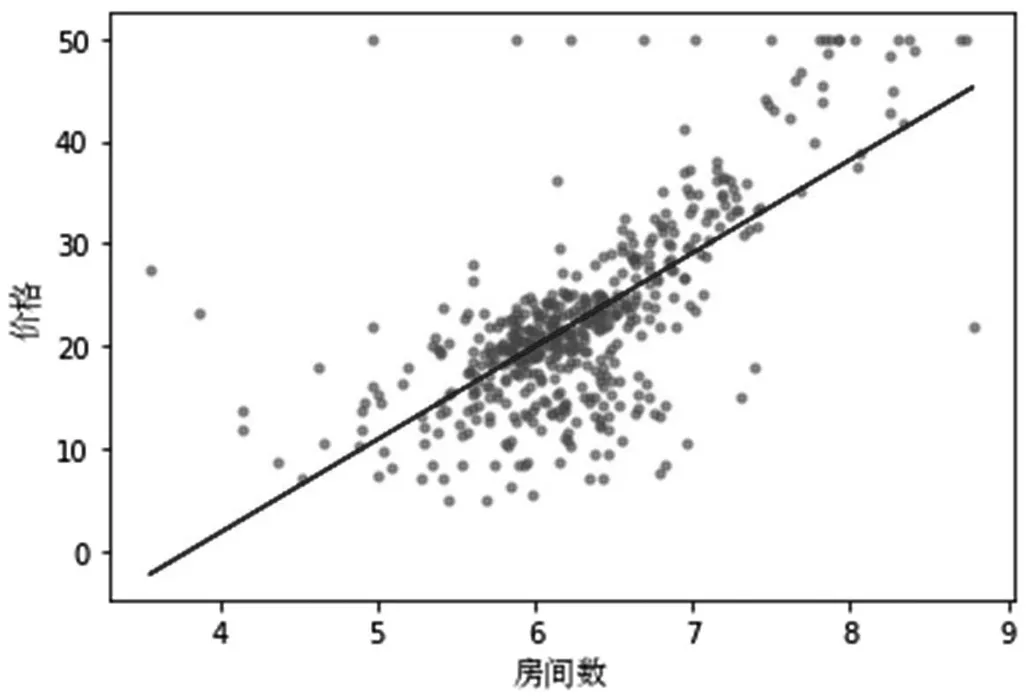
图2 线性回归分析图

(二)逻辑回归实验

逻辑回归其实是一个分类问题，在这里同样采用癌症数据，行逻辑回归分析，得到结果如下表：

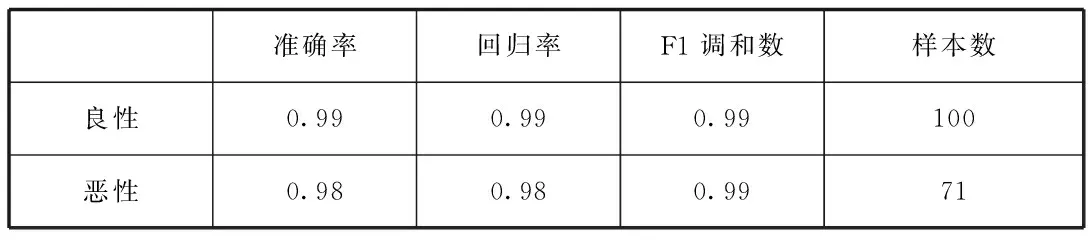
表1 癌症数据的逻辑回归

四、总结

通过两个实验，我们可以清楚的发现线性回归和逻辑回归的适用场景的区分，线性回归主要是处理回归问题，其预测结果是连续的数值，而逻辑回归实质是一个分类问题。本文主要讲述了两种回归的基础原理和实现。后序将展开逻辑回归在多分类问题的研究。