预应力锚杆复合土钉支护结构稳定可靠度研析

(郑州工业应用技术学院建筑工程学院 河南 郑州 451100)

一、引言

复合土钉支护结构作为一种新的支护方法，在城市基坑支护中得到了广泛的应用[1-2]。目前复合土钉支护结构的稳定性分析大多采用极限平衡法定值计算方法[3]，而土体力学参数的随机性使得定值计算方法的结果具有一定的不确定性，因此应考虑岩土力学参数的随机性，对其进行可靠性分析和计算。近年来，许多专家把可靠性理论引入到基坑稳定性计算中，进行了基坑与边坡稳定性的可靠性研究[4-5]。但对于黄土地区基坑预应力锚杆复合土钉支护结构稳定性可靠性分析的研究较少。因此，本文根据极限平衡理论，假定滑动面为抛物线形，通过Monte Carlo 重要抽样法对极限状态功能函数进行了可靠性分析。

二、基坑稳定性分析

(一)基本假定

对预应力锚杆复合土钉支护结构进行稳定性分析时，作基本假定为：

1.设滑移面为抛物线形；

2.C点处滑移面切线方向与水平线的夹角θC<900,且大于arctan(H/Xc)；

3.锚杆和土钉在滑面破坏时达到极限抗拉力；

4.土条之间条间力相互作用平衡合力为零。

(二)基坑内部整体稳定性分析

复合土钉支护稳定性分析计算简图如图1所示，图中坡脚O为坐标系原点；C点为滑移面与坡顶的交点；θC为过C点的滑动面切线与水平方向的夹角；B为土条底部弧长的中点；F为抛物线焦点；H为基坑深度；β为基坑坡角。根据假定条件，整体稳定性验算采用极限平衡理论的条分法。

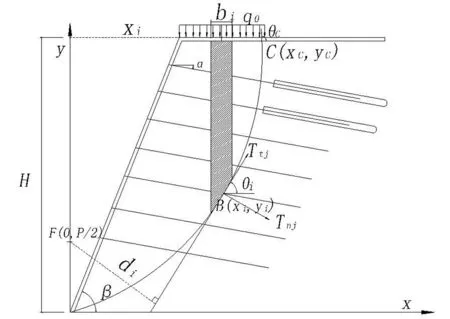
图1 复合土钉稳定性分析计算简图

(三)危险滑动面搜索

通常方法搜索出最危险滑动面可以满足工程要求的精度，但不能达到最优化的状态，有时会存在比较大的误差，遗传算法(GA)具有精度高和全局优化的优点，因此，滑动面采用遗传算法进行搜索。滑移面通过坡脚，这样决策变量的组成便成为XC和θC，安全系数Ks可以看作是XC和θC的函数，则无约束优化问题可表示为

(2)

采用MATLAB遗传算法工具箱编制程序进行搜索，通过确定决策变量XC和θC的大小来找出抛物线滑动面的焦点位置，从而确定最危险滑动面。

三、可靠性分析

(一)功能函数的导数

根据试验统计分析，重度γ的均值和变异系数对边坡的可靠性影响较小，c、φ的变异性对边坡可靠性影响较大，为简化计算选取土体的力学参数ci、φi、qsik作为复合土钉基坑支护体系可靠性分析的随机变量，在分析中各随机变量均服从正态分布。预应力锚杆复合土钉支护结构可靠性分析的功能函数对各随机变量的导数为

(3)

(二)可靠性计算方法

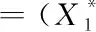
(4)

(5)

(6)

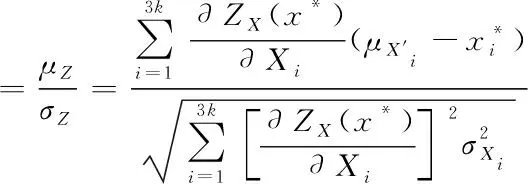
(7)

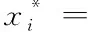
(8)

根据公式(4)～(8)计算体系的设计验算点和可靠度指标β。当X的各变量Xi之间相互独立时，求出样本vi=(vi1,vi2,…vik)T的无偏估计值，计算公式为

(9)

(10)

在体系的计算中，PVj(v)取正态分布的概率密度函数，V的均值和标准差分别取成x*,σX,根据公式(4)～(10)编制计算程序进行计算求得可靠度失效概率。

四、实例分析

甘肃省总工会办公楼及住宅楼位于兰州市城关区广场东口，场地北临农民巷，南侧为职工大厦，西临东郊巷，东侧为省民委宗教局，地貌单元划属黄河南岸Ⅱ级阶地。基坑开挖深度约9.5m，由于基坑四周支护方式的不同，选取基坑南侧的预应力锚杆复合土钉支护结构作为分析对象，锚杆孔径150mm，花钢管土钉孔径100mm，土钉墙钢筋网采用双向Φ6.5mm，间距为250mm×250mm，喷射混凝土厚度80mm，喷射混凝土强度等级C20。结构剖面图见图2，土层力学参数的数学统计特征值见表1,μc、μφ、μqsik分别为c、φ、qsik的均值，δc、δφ、δqsik分别为c、φ、qsik的变异系数。

表1 土层力学参数的数学统计特征值

图2基坑南侧支护剖面图

经计算，基坑稳定性可靠性分析结果见表1，计算结果为土体个力学参数在服从正态分布的情况下得到，蒙特卡罗重要抽样法可靠性计算结果与JC法、蒙特卡罗直接抽样法的结果对比分析，结果数值大小处于二者之间，在计算过程中，该方法比两者效率更高，结果表明，蒙特卡罗重要抽样法具有有效性和较高的计算效率。

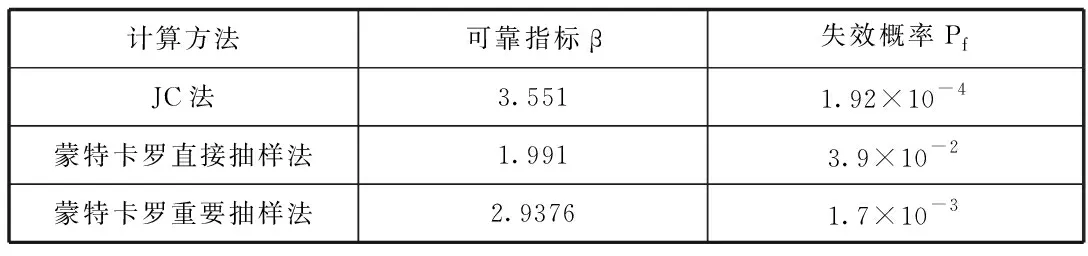
表2 可靠性分析结果

根据土体力学参数分布情况对基坑可靠性的影响，采用蒙特卡罗重要抽样法分别计算分析当一种参数服从对数分布时，另外两种参数服从正态分布，分三种模式来计算基坑可靠性的失效概率，计算结果见表3。

表3所示，模式1中的计算的可靠性失效概率与表2中的蒙特卡罗重要抽样法计算结果相比要小，可靠性程度要高，说明在基坑可靠性分析中力学参数c采用对数分布更合理。模式2和模式3的计算结果说明参数φ、qsik采用正态分布对体系的可靠度结果有利。

表3 力学参数分布类型不同的计算结果

图3 Pf与变异系数的关系

图4 β与变异系数的关系

图3所示为两层土的力学参数c、φ、qsik的变异系数对失效概率Pf的影响分析，由图中可知，失效概率随变异系数的增大而增大，φ和qsik的变异系数对失效概率的影响比较大，在变异系数小于0.3时，φ和qsik的变异系数对失效概率的影响程度后者要大于前者，在大于0.3以后，φ的变异系数对失效概率的影响明显要大于qsik的影响。c的变异系数对失效概率的影响最小。

图4所示为两层土的力学参数c、φ、qsik的变异系数对可靠度指标β的影响分析，从图中可以看出，β随变异系数的变大而减小，与赵延林等[6]针对同一土层做分析的结果一致，其中，粘聚力c的变异系数对可靠度指标β的影响最大，φ、qsik的变异系数对可靠度指标的影响较小，影响程度差不多。

对比图3和图4的分析结果，力学参数c、φ、qsik的变异系数对失效概率和可靠度指标的影响，总体遵循Pf和β的关系，力学参数变大，Pf变大而β变小的规律，其中，不同的是φ的变异系数对Pf影响最大，而c对β变化影响最大，与Pf和β两者之间的关系不一致。

五、结论

根据边坡的极限平衡理论和条分法，提出的一种基于可靠性理论的预应力锚杆复合土钉支护结构基坑稳定性的分析方法，并通过工程实例进行分析，分析表明：

(1)土体力学参数c、φ、qsik的分布类型对可靠度分析的失效概率Pf和可靠度指标β影响较大，参数c采用对数分布，φ、qsik采用正太分布计算的可靠度结果有利。

(2)土体力学参数c、φ、qsik的变异系数对基坑稳定性可靠性分析的失效概率Pf影响较大，随随变异系数的增大而变大，其中，内摩擦角φ对其影响最大。

(3)土体力学参数c、φ、qsik的变异系数对基坑稳定性可靠性分析的可靠度指标β影响较大，随随变异系数的增大而减小，其中，粘聚力c对其影响最大。