钛合金锥形压痕约束因子和代表应变的确定

2018-11-23吉喆高二庆沈承金宋庆雷徐杰郭涛

精密成形工程 2018年6期

吉喆，高二庆，沈承金，宋庆雷，徐杰，郭涛

（1.中国矿业大学，江苏徐州 221116；2.徐州巴特工程机械股份有限公司，江苏徐州 221004）

钛合金具有高比刚度、高比强度等优良的综合力学性能，在航空、航天领域得到广泛的应用[1—2]。压痕技术测量材料性能具有制样简单、操作方便、无损等优点，从而广泛应用于钛合金性能检测[3—4]。压痕测试技术是将压头压入被测材料，通过连续记录压头加载过程和卸载过程的载荷、位移数据，得到载荷-位移曲线的一种方法。通过分析载荷-位移曲线，不仅可以得到被测材料的弹性模量和硬度，而且通过量纲分析和压痕变形过程有限元分析，可以由载荷-位移曲线反求应力-应变曲线[5]。这对求解微小体积试样的应力-应变曲线，以及表征钛合金部件不同位置由于变形不均匀等原因引起的性能不均匀提供了一条可行便捷的方法。

通过载荷-位移曲线反求被测材料的应力-应变曲线时，代表应变（εr）是一个重要的参数。代表应变在材料应力-应变曲线上对应的应力称为代表应力（σr），代表应力与材料的硬度（H）存在以下关系：

式中：C是一个常数，称为约束因子。

通过使用代表应变和约束因子可以简化应力-应变曲线的求解，因而大量工作对这两个参数进行了研究。Tabor等[6]研究了不同预应变条件下低碳钢和铜的维氏硬度与拉伸应力的关系，发现以不同预应变条件下合金的硬度除以3.3为应力值，然后以对应的预应变值加上 0.08为应变值，这样处理的应力和应变点与合金的应力-应变曲线正好重合，因此指出代表应变为 0.08，约束因子为 3.3。Mata等[7]针对 Tabor提出的硬度和代表应力关系，采用弹塑性有限元分析了不同弹性模量、屈服强度和应变硬化指数条件下硬度和代表应力的关系，指出代表应变为 0.1，此时对应的约束因子为2.7。Keist等[8]通过最小二乘拟合分析，研究了Ti-6Al-4V合金维氏硬度与屈服强度（σy）和抗拉强度间（σUTS）的关系，发现维氏硬度与屈服强度和抗拉强度之间存在线性关系，即存在关系σy（或者σUTS）=H/i+j，其中i为比例常数，j为修正项。Tiryakioğlu等[9]研究发现维氏硬度与屈服强度关系之间修正项通常为负值，而维氏硬度与抗拉强度关系之间修正项通常为正值，因此会有维氏硬度与存在于屈服强度与抗拉强度之间某一应力之比修正项为0，此应力对应的应变为代表应变，采用此方法求出的代表应变为 0.024。这些研究力求确定统一的代表应变和约束因子值，然而不同研究结果得到的值不同。如果采用近似的代表应变和约束因子来求解应力-应变曲线，会导致较大的误差[10]，因此，为了确定适用于钛合金的代表应变和约束因子，还要进行深入研究。Hernot等[11]通过弹塑性有限元，分析了不同屈服强度和应变硬化指数条件下，压痕塑性区对应的代表应变，发现压痕代表应变和约束因子是随材料性能变化而变化的，并不存在一个统一的值。Branch等[12]和Prasad等[13]通过有限元模拟发现不同材料性能条件下，压痕塑性区应变分布不同，因此采用压痕塑性区应变的体积平均作为代表应变。这样定义的代表应变随材料性能变化而变化，没有统一值。这些研究指出代表应变和约束因子是随材料性能变化而改变，但是并没有给出代表应变和约束因子随材料性能变化的关系，不便于这两个参数的使用。

文中以Ti-6.5Al-3.5Mo-1.5Zr-0.3Si(TC11)合金为研究对象，通过热处理实验调控合金的性能，得到合金性能的变化范围。在此基础上，通过锥形压痕变形过程弹塑性有限元分析和压痕硬度分析，得到代表应变和约束因子与TC11合金性能参数间的定量关系，为通过压痕测试求解TC11合金的本构曲线奠定基础。

1 材料与方法

材料为TC11钛合金，合金棒材直径为100 mm。从合金棒材中线切割截取尺寸为 130 mm×26 mm×12 mm的热处理矩形试样，在其表面涂满玻璃润滑剂，然后放入箱式电阻炉中进行加热，以防止实验过程中试样表面发生氧化。热处理实验分为一步热处理和多步热处理以调控合金的性能。一步热处理是将试样分别加热到940,960,980,990,1020 ℃，保温30 min，然后空冷或者水冷。多步热处理是在一步热处理水冷后进行强韧化处理[14]。

热处理后，在每个矩形坯料中线切割截取3个拉伸试样。拉伸试样标距为35 mm，厚度为2 mm。采用 CMT-5305电子万能拉伸实验机测量试样的拉伸性能，拉伸速度为2 mm/min，采用引伸计测量试样的变形量。3个试样的平均结果作为试样的最后性能。

4种典型试样的热处理工艺和性能见表1，拉伸曲线见图1。采用幂强化模型来描述合金的应力-应变曲线[4,15]，见式(2)。

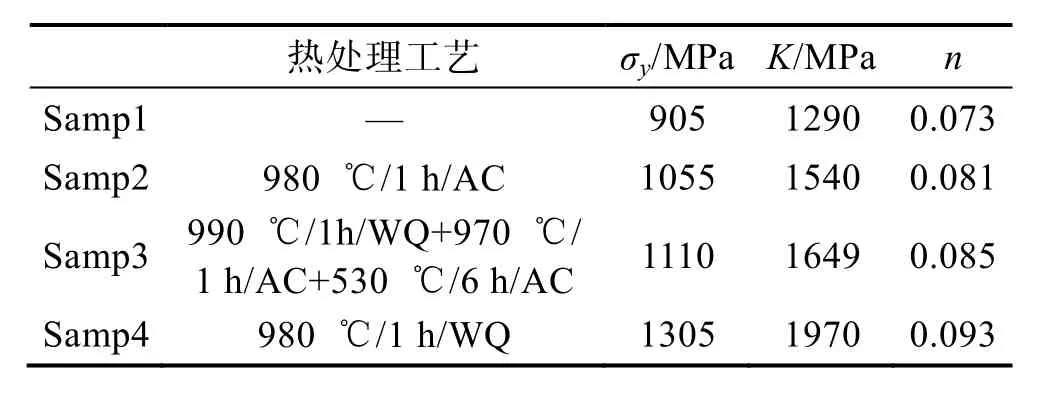
表1 TC11合金的热处理工艺参数和力学性能Tab.1 Technological parameters and mechanical properties for heat treatment of TC11 alloy

图1 TC11钛合金拉伸试样的真应力-真应变曲线Fig.1 True stress-strain curves of TC11 tensile samples

式中：E为弹性模量；K为硬化系数；σy为屈服强度；n为应变硬化指数。

由应力-应变曲线弹塑性段连续可得：

通过拉伸曲线计算得合金的弹性模量为 110 GPa，σy,K和n值见表1，其中AC为空冷，WQ为水冷，这些性能参数涵盖了实验中合金性能的范围。

在热处理后的试样中线切割截取10 mm×10 mm×6 mm的压痕试样。对压痕试样进行镶嵌，然后用金相砂纸进行打磨，最后进行抛光处理。对抛光后的试样用瑞士的 CSM 压痕仪进行实验，压头为锥形的Berkovich压头。压痕最大载荷为4.9 N，每个试样压痕试验重复5次。

2 压痕变形过程有限元模型建立

压痕变形过程采用Abaqus有限元分析软件进行模拟，采用三棱锥形Berkovich压头，已有大量文献证明，在有限元建模时可以采用半锥角为70.3°的圆锥压头代替[5,16—17]。圆锥压头压入材料过程是一个典型的轴对称问题，因此采用二维轴对称模型进行模拟。建立的 Abaqus几何模型见图2。由于模型的对称性，金刚石压头用一条线表示，被压TC11材料用一个平面表示。平面的左边施加对称边界条件，底边限制竖直方向的位移，载荷通过压头的参考点施加。由于四节点轴对称线性减缩积分单元（CAX4R）适用于大变形分析，而且具有较高的计算精度，适合压痕变形过程有限元分析，因此，采用CAX4R对被压材料进行网格划分，共划分7268个单元。此外，压痕变形过程大变形区域集中在压头附近，因此采用网格尺寸渐变方式划分网格，在压头附近采用尺寸较小的网格（0.5 μm×0.5 μm），而在远离压头的位置采用尺寸较大的网格。这样划分网格既可以获得较高的计算精度，也可以节约计算时间。

模拟结束后，通过压头参考点处的载荷和位移，求出压痕变形过程载荷-位移曲线。采用表 1所示材料性能参数进行压痕变形过程有限元模拟，得到的载荷-位移结果见图3，其中也包含了实验的载荷-位移曲线。由图3可见，模拟结果与实验结果吻合良好，表明建立的模型可以用于压痕变形过程分析。

3 结果与讨论

3.1 压痕硬度计算

在进行TC11合金压痕变形有限元模拟时，弹性模量取110 GPa，屈服强度取13个值，分别为800,850,900,950,1000,1050,1100,1150,1200,1250,1300,1350,1400 MPa，应变硬化指数取9个值，分别为0.04,0.05,0.06,0.07,0.08,0.09,0.1,0.11,0.12，共有117个组合，这些组合范围完全覆盖了表1中实验测量的TC11合金性能。采用这些性能参数，通过压痕变形过程有限元模拟可以得到TC11合金载荷-位移曲线。压痕硬度和弹性模量可以通过压痕曲线分析得到。考虑压痕载荷-位移曲线卸载部分的弹性回复，Oliver和Pharr将卸载曲线压痕表示为[18]：

式中：P为载荷；hf为卸载后的残余压痕深度；B和m为拟合参数。

由式(4)可以求得卸载曲线的接触刚度S为：

式中：hmax为最大压痕深度。

在最大压痕深度处，压头和材料接触深度hc为：

式中：γ为压头形状参数，对于Berkovich压头，其值为0.75。

通过接触深度可以得到压头与材料的接触面积A为：

压痕硬度为：

式中：Pmax为最大载荷。

图3 实验和有限元模型计算的压痕载荷-位移曲线Fig.3 Indentation load-penetration depth curves of experiment and FEM computation

通过卸载刚度S和接触面积A，可以得到等效弹性模量为：

式中：ω是非对称压头修正系数，对于Berkovich压头，其值为1.034。

由式(9)可以求得被压材料的弹性模量为：

式中：ν为被压材料泊松比；Ei和νi分别表示压头的弹性模量和泊松比，金刚石压头的值分别为1141 GPa和 0.07。

屈服强度随压痕硬度变化关系见图4，可见硬度随屈服强度的增加而增加。在模拟性能参数范围内，压痕硬度从3000 MPa变化到5000 MPa，变化范围较宽。对屈服强度和压痕硬度进行最小二乘回归拟合，可得：

式中：i和j分别为2.97和271。

图4中实线为最小二乘回归分析结果，虚线为剩余标准差，拟合优度为0.94，表明屈服强度和压痕硬度之间符合线性关系。Keist等[8]分析了Ti-6Al-4V合金屈服强度和压痕硬度，发现两者之间也存在线性关系。这个结果表明相对于应变硬化指数，屈服强度对合金硬度的影响更加显著。这是因为应变硬化指数较小，而文献[8]中应变硬化指数值更小（0.032～0.052），应变硬化指数值的变化引起的硬度变化较小。文献[8]中i和j分别为3.6和90，和文中计算结果不同，这可能是由于材料性能不同引起的。Ti-6Al-4V的屈服强度（700～1000 MPa）和硬度（3000～3800 MPa）范围都在本文性能值范围的下限，可见对于不同的材料性能范围，参数i和j需要重新计算。

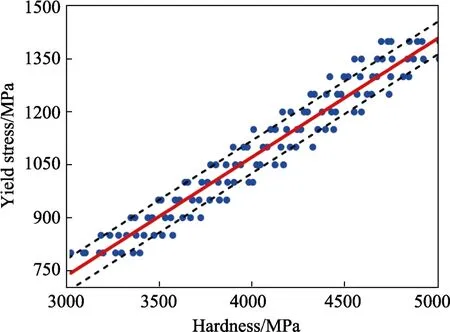
图4 屈服强度和硬度关系Fig.4 Relationship between yield stress and hardness

3.2 屈服强度对约束因子和代表应变的影响

约束因子和代表应变可由硬度与材料性能参数关系求出。由式(1)—(3)可得：

对式(12)两边同时取自然对数可得：

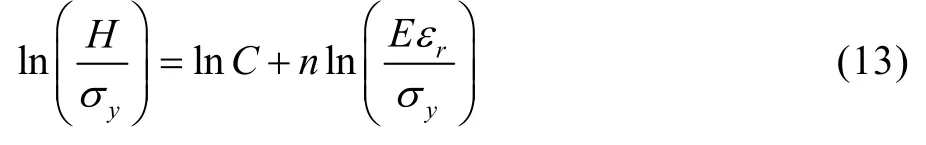
式(13)中以n为自变量，ln(H/σy)为因变量，对不同σy值进行拟合。如果C和εr为常数，则拟合结果为直线。通过直线的斜率和截距可以分别计算出εr和C。

不同屈服强度条件下，式(13)的拟合结果见图5。由图5可见，不同屈服强度条件下，ln(H/σy)与n均呈现线性关系，拟合优度均高于0.98，而且这些拟合直线大致保持平行，说明不同屈服强度条件下，代表应变变化很小。此外，拟合直线的截距随着屈服强度的增加而减小，表明约束因子也随屈服强度的增加而减小。这些结果说明约束因子和代表应变的确随材料性能参数变化而变化，并不存在固定值。而且，这两个参数对材料性能参数依赖关系是不同的。屈服强度会显著影响约束因子，但是应变硬化指数对约束因子影响较小，而屈服强度和应变硬化指数对代表应变影响都很小。

图5 ln(H/σy)和应变硬化指数(n)关系Fig.5 Relationship between ln(H/σy) and strain hardening exponent (n)

通过图5拟合结果求出的约束因子和代表应变见图6。由图6a可见，约束因子随屈服强度增加而呈线性减小。通过最小二乘拟合得到约束因子与屈服强度间的关系为：

当屈服强度为800 MPa时，约束因子为3.56；而当屈服强度为1400 MPa时，约束因子为3.19，平均值与Tabor提出的3.3非常接近。DiCarlo等[19]基于有限元分析，研究了Tabor提出的通过约束因子和代表应变求合金应力-应变曲线的方法，求解的低碳钢和铜的应力-应变曲线与实验结果比较吻合，因此Tabor提出的约束因子具有较高的精度。由图6a可见，约束因子是随材料性能变化而变化的。低碳钢和铜硬化指数均为 0.2，但是低碳钢弹性模量和屈服强度均高于铜，而屈服强度升高会导致约束因子会降低，可见低碳钢和铜约束因子相当，可能是由于两者弹性模量不同造成的。文中计算得到的约束因子最大值（3.56）和最小值（3.19）差别大于10%，对压痕硬度值下限3000 MPa计算代表应力，其结果相差将近100 MPa，误差非常大。

图6 约束因子和代表应变随屈服强度变化曲线Fig.6 Curve for constraint factor and representative strain change as a function of yield stress

图6b为代表应变与屈服强度关系，可见代表应变随屈服强度变化并不大，在平均值0.025附近波动。这个波动可能是由于ln(H/σy)与n的拟合误差引起的。代表应变 0.025与 Dao[5]提出的 0.033，Tiryakioğlu[9]提出的 0.024，Branch[12]提出的 0.035非常接近，而与Tabor[6]提出的0.08相差较大。代表应变的计算方法会影响代表应变的值[11]。文中和文献[5]中代表应变是超过屈服强度以后的塑性累积应变，文献[9]中代表应变定义为塑性应变，文献[12]中将代表应变定义为压痕塑性区塑性应变的体积平均，而Tabor代表应变是拉伸曲线上等效的应变，可见压痕代表应变会随计算方法而变化。

在求解约束因子和代表应变时，进行了数据拟合，因而存在一定的误差，需要进行误差分析。使用代表应变在应力-应变曲线上求解代表应力的准确值，然后通过式(11)和(14)用压痕硬度求解约束因子，再通过式(1)求解代表应力的计算值。代表应力计算值和准确值之间的误差见图7。由图7可见，绝大部分误差在±1.6%之间，说明计算得到的代表应力的准确度较高。

图7 代表应力误差分析Fig.7 Error of representative stress

3.3 弹性模量对代表应变的影响

图6中的约束因子和代表应变是在固定弹性模量（110 GPa）条件下求出的，然而钛合金的弹性模量也会随合金种类变化而变化[20]，因此，有必要研究弹性模量对钛合金约束因子和代表应变的影响。取弹性模量为70,90,130,150 GPa，分别对屈服强度和应变硬化指数的117个组合进行仿真模拟，采用式(13)对压痕硬度数据进行分析，求得的约束因子见图8。由图8a可见，约束因子在2.8到3.7之间，在Hernot得到的约束因子范围内[11]。此外，可见不同弹性模量条件下约束因子都随屈服强度的增加而线性减小。此外，从图8a可见，约束因子随弹性模量的增加而增加，因此在Tabor的研究中[6]，低碳钢和铜相同的约束因子，可能是低碳钢高的屈服强度引起约束因子减少，高的弹性模量引起约束因子增加，是两者的综合效果引起的。

图8中求出的约束因子是屈服强度的函数。为了方便约束因子的使用，需要求出不同弹性模量条件下屈服强度和压痕硬度的关系。通过最小二乘回归分析发现不同弹性模量条件下，屈服强度和压痕硬度都满足式(11)，只是式中常数不同，因此，综合式(11)和(14)，约束因子可以表示为：

式中：p,q,i,j为常数，其值见图8b。由图8b可见，在式(15)的4个常数中，p和i随弹性模量的增加而增加，q和j随弹性模量的增加而减小。

图8 弹性模量对约束因子的影响Fig.8 Effect of elastic modulus on constraint factor

图9 弹性模量对代表应变的影响Fig.9 Effect of elastic modulus on representative strain

不同弹性模量条件下，约束因子的计算结果见图9。由图9可见弹性模量从70 GPa增加到150 GPa，约束因子的值从 0.029降低到 0.023，而且降低的幅度越来越小。采用图7中类似的方法，对不同弹性模量条件下的约束因子和代表应变进行误差分析，误差在±3%之间，这说明文中提出的方法可以得到较为准确的约束因子和代表应变。