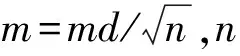基于全站仪自由设站基准线法水平位移测量精度分析

喻 兵

(上海勘察设计研究院(集团)有限公司，上海 20438)

0 引 言

水平位移测量方法一般是采用视准线法、极坐标法、小角度法、前方交会法等，而这些方法的测站点固定(对中误差影响测量精度)，测点间通视要求较高(作业效率较低)；以城市工程项目为例，施工环境非常复杂，施工围挡内空间往往非常狭窄，同时场地内机械及堆放的建筑材料等对通视造成严重影响，常规的监测方法受到很大的限制[1-2].本文介绍的这种基于全站仪自由设站的基准线法水平位移测量方法，该方法具有测站点摆放灵活、无需对中，能有效规避对中误差的影响及通视等问题的限制，并能显著提高测量的速度和精度.

1 测量方法

根据监测对象，在与所测水平位移方向大致垂直的方向布设一条水平位移测量基准线(平面直线).具体布设方法为：在监测对象两端稳定区域布设基准点(A、B)，基准点为固定标志，可设置在开阔的场地，亦可设置在稳定的建(构)筑物上[3].基准点确定的空间基准线投影到水平面即为水平位移测量基准线(见图1).

外业测量时，在基准线概略中部方便观测的位置架设测站(测站位置与基准点和尽可能多的监测点通视)，无需对中和定向，测量基准点A、B和各监测点在同一独立坐标系下的坐标(周期性观测时坐标系无需一致).通过点到直线距离公式即可计算各监测点到基准线的水平距离d(见图1)，周期性观测计算的水平距离变化(Δd)即为各监测点的水平位移变化.

当无法一次性完成所有监测点的测量时，可重新选择合适的测站位置测量剩余监测点，新测站仍需与基准点A、B通视，整平后测量基准点与待测监测点在同一独立坐标系下坐标即可(无需与其他已测测点坐标系一致).计算时根据不同的坐标系，各监测点须分开计算.

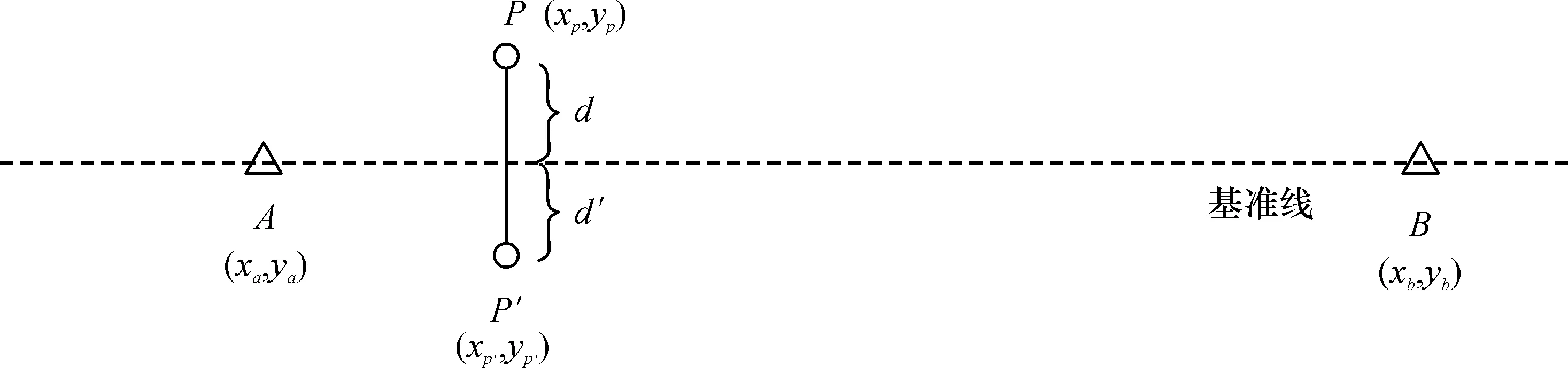
图1 全站仪自由设站基准线法水平位移测量示意图

2 计算方法

已知某次测量A、B、P点坐标分别为(xa，ya)、(xb，yb)、(xp，yp)，根据点到直线距离公式(1)，推导历次测量距离值的计算公式(2).

(1)

式(1)中：直线方程为Ax+By+C=0，点P的坐标为(xp，yp).

(2)

考虑监测点一般分布在基准线两侧，为便于水平位移量计算和变形方向的判别，式(2)相对于式(1)无绝对值符号，计算出的距离值正负代表在基准线的两侧.例如某次测量时各点的坐标值输入Excel，通过在Excel内编辑计算公式，能快速计算各测点相对于基准线的距离d，示例(见表1).

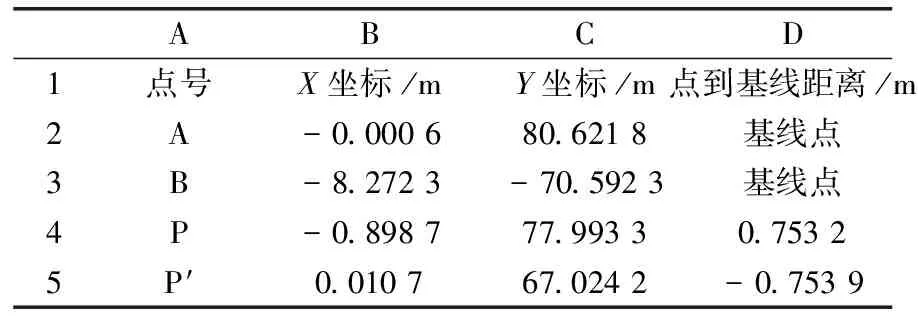
表1 点到基线距离计算表

注：Excel内编辑，1-5、A-B分别代表行列号

为便于判断变形方向，通过在Excel内编辑公式，将各点批量展绘到AutoCAD中，根据各监测点与基准线的相互关系(分布在基准线的哪一侧)，结合所测水平位移方向，即可较为方便地判断各监测点的距离值变化量正负所表示的水平位移方向.

Excel内点到基线距离计算公式：=ROUND((($C$3-$C$2)×B4+($B$2-$B$3)×C4+($C$2×$B$3-$C$3×$B$2))/(($C$3-$C$2)^2+($B$2-$B$3)^2)^0.5,4).

Excel内点坐标批量展绘到AutoCAD中公式：="POINT"&C2&","&B2&"-text"&C2+0&","&B2+1.5&"1.00"&A2.展绘步骤：先复制excel表中公式单元格(可以所有点一起复制)，然后粘贴到AutoCAD下方命令行内即可.

3 精度分析

式(2)中分母为基线长，假定两端基准点稳定，则可认为基线长为常数D.为便于误差分析，假定测量时的独立坐标系y轴与基线平行，即xa=xb，ya-yb=D，即式(2)可简化为：

d=xa-xp

(3)

假设斜距s，水平角α，垂直角β，则：

x=s×cosα×cosβ

(4)

在常规项目的水平位移监测，垂直角一般均在±10°范围内，即0.97≤cos2β≤1，

式(4)可近似改写为：

x=s×cosα

(5)

对式(5)求微分得：

dx=cosα×ds-s×sinα×dα

(6)

由误差传播定律可得：

(7)

式(7)中，ms与mα分别为全站仪的测距和测角精度，可通过全站仪的精度指标确定.

设xa、xb为同精度观测，则有：

(8)

当采用徕卡TS30全站仪，测角精度ma=±0.5″，测距精度ms=±(0.6 mm+1 ppm)，根据式(8)估算边长为50 m、100 m、150 m时，距离d的测量中误差如下：

若S=50 m，则-0.65≤mx≤0.65 mm，-0.92≤md≤0.92 mm；

若S=100 m，则-0.70≤mx≤0.70 mm，-0.99≤md≤0.99 mm；

若S=150 m，则-0.75≤mx≤0.75 mm，-1.06≤md≤1.06 mm.

当s=150 m时，合计测量范围可达300 m，且精度与《建筑变形测量规范》(JGJ8-2016)内一等水平位移监测精度相当(坐标中误差±1.0 mm)[4].

4 精度试验

4.1 概况

在某条1996年竣工的公路隧道下层(相对封闭，气象环境稳定)选择长度约150 m的区段作为试验段，试验期间该段隧道周边无施工，可认为该段隧道在水平方向无变形.[5]共布设2个基准点，基线长151.440 7 m；23个监测点，监测段长度112.547 6 m，监测点距离基线距离1.546 5～5.398 2 m之间[6]；基准点和监测点均为固定测量标志(小棱镜)，仪器采用了5台相同型号的徕卡TS15全站仪(测角精度±1″，测距精度±(1 mm+1.5 ppm)).

为尽量模拟日常测量，历次测量均在不同日期的相同时间段内进行，在测区中部位置架设仪器，利用全站仪自动照准和自动记录读数功能，测量各点坐标值.每次测量测回数为1，每次测量时长平均约为6 min，共进行了16次独立测量，持续时间约3个月.

4.2 实测精度分析

根据式(2)和表1内公式，将16次独立测量成果计算整理(见表2—3).

为提高测量精度，16次独立测量的测量人员相同、仪器型号相同、环境条件相近、观测时段相近、观测方法相同、数据处理方法相同，同时可以认为历次观测为等精度观测，根据中误差计算公式，各点测量中误差算结果(见表2—3)[7].

表2 16次独立测量成果表

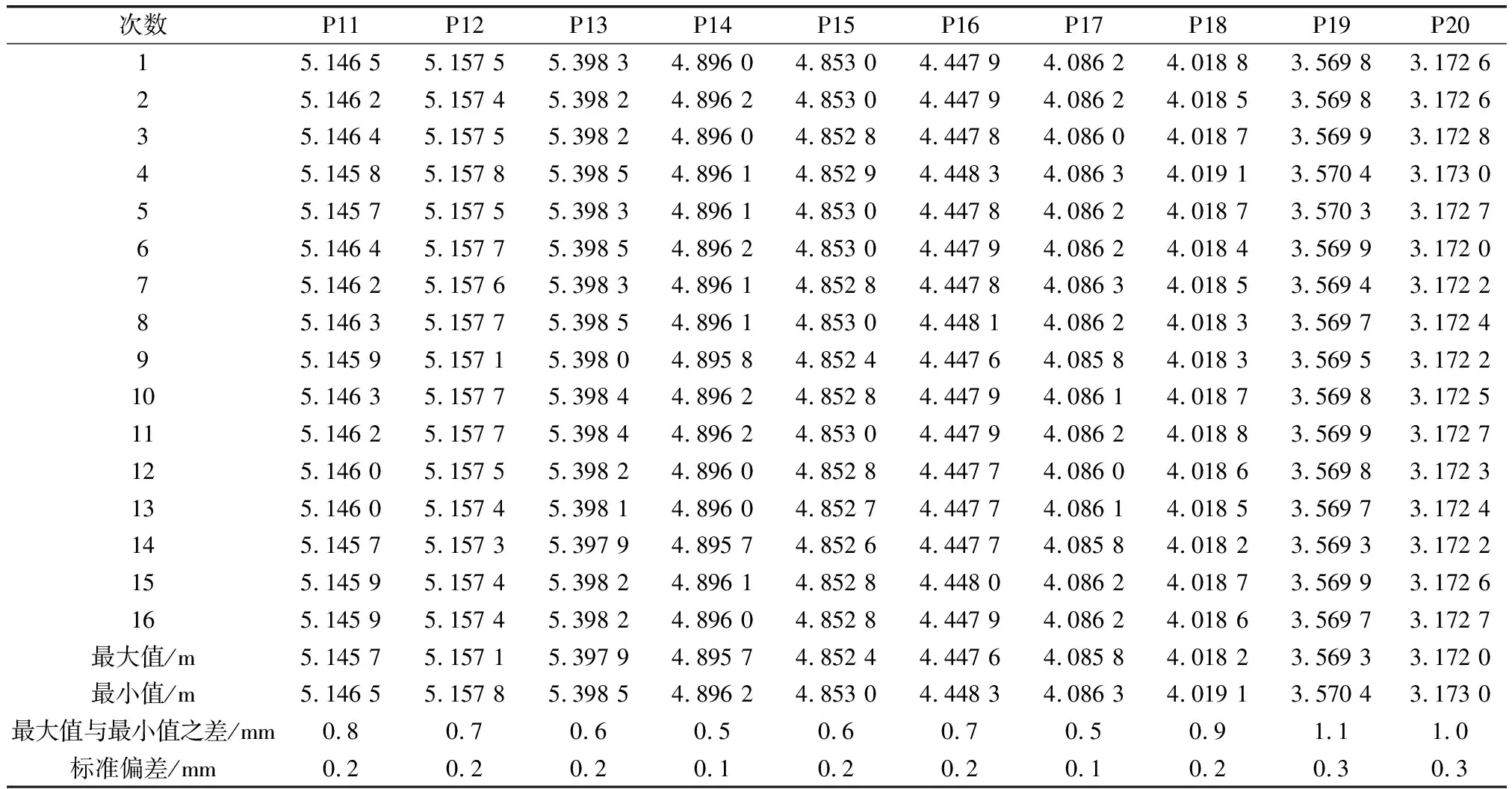
表3 16次独立测量成果表

(1)根据仪器测距精度±1.1 mm(s=75 m)和测角精度±1″，按前述式(7)、(8)计算得到距离d的测量误差md≤1.57 mm；表2中10个点的16组成果数据计算的标准偏差最大为0.3 mm，约为md的1/5，实际测量精度远远高于理论推算精度，与《建筑变形测量规范》内特等水平位移监测精度相当(坐标中误差±0.3 mm)[4].

(2)取各点前2次测量成果值平均值为初始值，根据各点14次测量成果值，计算各点历次监测次变化量Δd，根据变化量分布区间整理统计(见表4).

表4 各点历次监测次变化量Δd发布区间统计表

注：Δd总个数为280个，其中最大值为0.9 mm.

变化量|Δd|≤0.5 mm的个数占比达92%，根据《建筑变形测量规范》规定取变形允许值的1/10～1/20作为位移量的测定中误差[4]，本次试验精度达到变形控制值为5 mm的监测等级要求；如需进一步提高测量精度，可通过增加施测的测回数实现.[8]

(3)16次试验测量共采用了5台相同型号全站仪，从标准偏差的大小和次变化量Δd的分布区间可以看出，不同仪器间测量成果相差不大，说明历次监测可以利用同型号仪器替换测量.本次试验由于受条件限制，采用的5台仪器为相同型号，不同型号仪器替换测量有待验证.

5 结论与建议

根据上述分析，此方法不论其工作效率还是在精度方面均具有较好的工程实用价值，并得出以下结论和建议：

(1)此方法消除了仪器的对中误差，如果测点安装固定标志，则测点的对中误差也可消除.

(2)基准点和监测点均埋设固定测量标志，测站点无需对中和定向，历次测量只需一人即可完成(其他测量方法需2～4人)，节省人工，具有较好的经济效益.

(3)此方法测量过程便捷高效，非常适合在地铁轨行区、市政隧道、高铁等对测量时间有严格要求的场所进行快速测量.

(4)当监测对象为曲面时，采用本方法时应根据测量方向和变形方向，应将测量值根据待测水平位移方向进行矢量分解.

(5)对于在遮挡物较多的区域测量时，可灵活架站，当无法一次性完成所有监测点的测量时，可重新选择合适的测站位置测量剩余监测点.

(6)配合全站仪自动化监测，可以作为解算水平位移的一种方法.

(7)根据《建筑变形测量规范》内相关内容，二等水平位移要求采用的全站仪标称精度不低于测角±1″，测距±(1 mm+2 ppm)；本次试验采用仪器精度与上述要求精度基本一致(测距精度与边长有关，边长较短情况下对测距精度影响不明显)，但试验测量精度远远超过规范要求二等位移测量精度，精度提升明显.