由点到面整体建构
——《20以内的进位加法(第一课时)》教学设计(二)
2018-11-23钱丽
钱 丽
20以内的进位加法,是在学生已经认识20以内的数,掌握10以内加、减法的基础上教学的。这部分内容在教材中通常被分成三部分:9加几;8、7加几;6、5、4、3、2加几。这样的编排,突出了由点到面、先慢后快、逐步建构的学习原则。但是,从学习内容的主线来看,“凑十法”是计算进位加法最基本、最重要、对后续学习具有“长远影响力”的方法。所以本课教学设计,试图对教材内容进行整合重组,以“凑十法”为主线,以“9加几”为基点,然后迁移类推到“8加几”“7加几”,紧紧抓住结构关联,使知识获得和能力发展呈现一条清晰的脉络,从而达到“见树木,更见森林”的整体建构效果。
【教学过程】
一、铺垫准备,激活思维
课件出示数学王国闯关的情境。口算:10+2、10+9、10+6、7+10、3+10。
师:你们怎么算得这么快?
小结:这些算式都是10加几的算式,10加几等于十几。
【设计说明:以口算抢答的形式复习10加几,有利于学生快速运用和强化“10加几等于十几”的学习经验,为后面教学20以内的进位加法需要用到的“凑十法”做好了铺垫。】
二、自主尝试,探究算法
1.教学 9+4,感知“凑十法”。
(1)算法多样化。
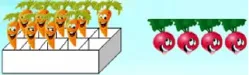
①寻找条件。
师:从上图中你看到了哪些数学信息?(板书:看)
(根据学生回答,在图形下方显示9和4)
②提出问题。
师:根据这些信息,你能提出一个数学问题吗?(板书:提)
(学生回答后用大括号表示“一共有多少个萝卜?”)
③解决问题。
列出算式“9+4=”后,让学生用圆片摆一摆,尝试计算,小组合作研究。(板书:摆)
学生完成操作后,交流汇报:
方法一:一个一个数出来。
方法二:从盒子的外面拿一个萝卜放入盒子里,就知道萝卜一共有13个。
方法三:10+4=14,10 里面少1 个,14-1=13。
方法四:9+1=10 10+3=13
……
(2)算法最优化。
师:这些方法中,你最喜欢哪一种?为什么?
师:为什么要从右边拿一个放进盒子里呢?
师:看来你们是把9凑成了10,把 9+4变成了 10+3,这样一移,就能让我们一眼看出9+4等于13了。
(3)算法图式化。
师:大家刚才想得很好,摆得也很好,那你能不能把刚才想的、摆的过程写出来呢?(板书:写)
(学生尝试书写,然后完善成以下图式)
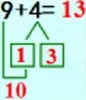
师:谁能看着算式再来说一说,怎样算9+4?(板书:说)
【设计说明:数学教学应该让学生的多种感官“动”起来,因此在解决问题的环节中,我设计了让学生用学具摆一摆、自主探索各种算法、合作交流优化算法的活动,从而经历解决问题的过程。通过“看、提、摆、写、说”这五步使学生在整体感知中形成“凑十”的表象,再把看得见的表象转化为图式,并及时内化为计算方法,最后通过语言表达出来,明白算理。】
2.尝试 9+8,揭示“凑十法”。
课件出示下图,对照刚才板书的“看—提—摆—写—说”的流程图组织教学。

师:你看到了什么数学信息?根据这些信息能提一个数学问题吗?怎么列式?
师:怎么算9+8呢?你可以摆一摆图片,也可以直接在图上圈一圈(板书:圈),然后把你的想法写出来。(学生独立完成后,交流汇报)
师:回顾刚才的学习,我们计算9+4,9+8有什么相同的地方?

小结揭题:我们都是把9凑成了10,再算“10+几”就方便了,我们把这种方法称为“凑十法”。(板书:凑十法)
3.巩固9+几,探索规律。
师:根据刚才的学习收获,完成这样一道加法题,看谁想得多,想得好,算得快。
(出示9+□=1□让学生推算,形成 9+1、9+2、9+3……9+9的算式表)
师:你发现了什么规律?得数的个位上为什么会比填的加数少了1呢?
【设计说明:从简单的摆一摆到直接的圈一圈,再到应用凑十法直接运算,学生认知的思维水平不断地提升。系统整理9加几的算式,不仅强化了凑十法的应用,更帮助学生实现了初步的认知建构,为后续更好地扩展到8加几、7加几并实现更大的建构做好了铺垫。】
三、迁移类推,丰富理解
1.小河里游来了两群鸭。它们各有多少只鸭呢?
第一群
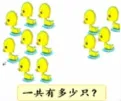
第二群
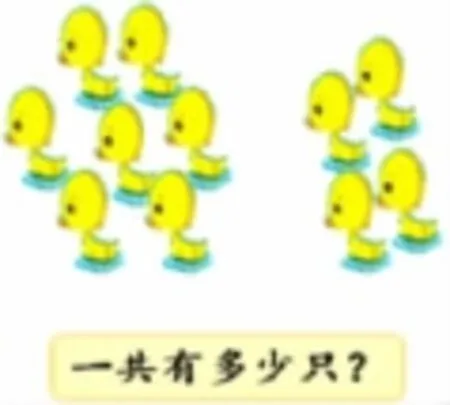
(学生自主尝试计算8+4、7+4后交流汇报,着重强调“凑十法”在“8加几”“7加几”的进位加法中的应用)
揭示课题:20以内的进位加法。
2.辨析比较 9+4、8+4、7+4。
师:同学们,为什么都是加4,都应用了“凑十法”,分法却不一样呢?
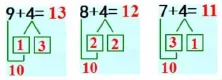
师:9加1等于10,把9凑成10,就要把4分成1和几;8加2等于10,把8凑成10,就要把4分成2和几;7加3等于10,把7凑成10,就要把4分成3和几。
【设计说明:迁移类推是重要的数学学习方法。由于学生有了“凑十”的经验基础,因而在计算8+4、7+4 时,很快就能把“凑十”计算方法进行类推,原有的认知建构在不知不觉中向前迈进了一大步。在最后的辨析比较中,学生不仅对“凑十法”有了更加深刻、丰富的认识,而且对20以内的进位加法具有了初步的、整体性的认识。】
四、系统练习,巩固新知
1.对比练习。
8+5= 7+2= 6+9= 7+7=
2.为卡车找家。
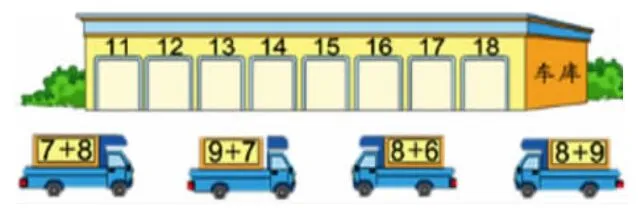
师:你们能帮这些卡车找到自己的家吗?这些卡车该停到哪些车库里呢?
(学生自主完成,然后汇报交流,让学生说说计算时的想法)
师:像8+9,我们可以把8凑成10,也可以把9凑成10。但是,“拆小凑大”更方便!
【设计说明:数学学习就是对已有认知结构的补充、调整和建构。第一道练习,意在培养思维的灵活性,比如,“9加几”也包含了“几加 9”,“8 加几”也包含了“几加8”。同时,学习了进位加法不能忘了不进位加法,能准确地加以区分也是学习目标之一。第二题“为卡车找家”重在突破难点,两个加数均为较大数的进位加法相对难度较大,而“拆小凑大”也渗透了巧算的思想。】
五、全课小结,揭示课题
师:回顾板书,今天我们学习的加法计算有什么特点?和以前学习的加法有什么不同?你还有什么疑问吗?
【设计说明:数学是“结构的科学”。数学知识的整体性、结构性、逻辑性对数学教学和儿童数学学习具有十分强大的引导性。本课学习体现出结构化学习的鲜明特征,从“整体”入手,抓“主线”突破,在“系统”中建构,让学生把“搬来的砖头都砌成了墙”,实现了对教材的超越,也体现出学习的简约化。】
