超大直径低壁浅仓圆环壳结构模型及其应用

唐寿高 王应安

(同济大学航空航天与力学学院应用力学研究所,上海 200092)

0 引 言

筒仓是贮存散体物料的理想仓型,它具有容量大,结构简单等优点,因此在现代物流、粮食、煤炭、水泥等行业中有着广泛的应用。以往设计的超大直径钢筋混凝土低壁浅仓结构主要有两种形式,即分缝式带扶壁柱的挡土墙和无缝无扶壁柱圆形挡土墙[1]。数10年来,我国水泥生产企业建造了大量的带扶壁柱的这种仓体,如图1所示为大量正在服役的内径80 m、壁高12 m～13 m的基于直线式挡土墙理论的煤炭、铁矿石等贮料筒仓。该仓上壁厚400 mm、下壁厚550 mm,仓壁外沿环向等间距分布60根变截面扶壁柱(上下端截面分别为b×h=500 mm×900 mm和500 mm×1 500 mm),每根扶壁柱底部设有桩基(钻孔灌注桩直径600 mm长不少于12 m),仓壁顶部设有环梁(截面1 000 mm×900 mm),底部设有基础梁(截面1 200 mm×1 800 mm)。

图1 带扶壁柱与桩基的基于直线式挡土墙理论的筒仓Fig.1 Silo based on the theory of linear retaining wall with pillar and pile

现有的无缝无扶壁柱圆形料仓,这种结构形式充分利用仓壁内环向钢筋承担堆料压力、温度应力等荷载,其受力要优于前者,且施工简单、外观简洁、材料利用率高,缺点是温度应力对仓壁造成较大影响,实际配筋量较大,经济效果不显著[1]。

近年来,上述超大直径浅仓力学分析与内力计算已有不少报道。笔者曾对特大型超低壁浅仓提出按圆柱壳弯曲理论的底部可滑动的力学模型[2],并曾应用于安徽铜陵海螺水泥有限公司直径80 m、高13 m的筒仓设计与建造,该结构现已安全服役十余年,效果良好。薛二伟[3]采用三维有限单元分析了仓壁厚度对大直径环筒式浅圆贮煤筒仓受力性能的影响;汪碧飞等[4]在含肋柱、环梁、承台等在内的筒仓上部结构与地基基础的相互作用的前提下,分析了季节温升与温降和堆煤引起的筒仓内外壁温差、煤压等主要荷载对筒仓结构的影响等;Yin Wang等[5]基于任意拉格朗日-欧拉公式用有限元分析了装卸料时仓壁压力问题。张振宇等[6]采用圆柱壳弯曲理论,分别对筒仓在贮料水平压力和温度作用下的仓壁内力及底部约束的边缘效应进行了分析,并与有限元计算结果进行了对比。

关于现有圆形筒仓的边缘效应,现行的《钢筋混凝土筒仓设计规范》(GB 50077—2003)(以下简称《规范》)[7]中规定“对于圆形筒仓或浅圆仓,在远离固定端或约束区的仓壁内力,可按无矩理论(薄膜理论)计算,但是在仓顶与仓壁、仓壁与仓底以及仓壁与基础等整体连接部位,尚应计算其对仓壁约束的边缘效应。”另外,关于筒仓仓壁的温度作用,《规范》第4.1.1条规定“直径21～30 m的筒仓可按其最大环拉力的6%计算,直径大于30 m的筒仓可按8%计算。”

有关大直径低壁浅仓的内力及温度应力分析等还有许多报道,另外关于仓壁内散料压力荷载分布形式实验研究和计算分析等也文献众多均不一一列举。总之,尚未见对上述超大直径低壁浅仓提出其他不同的结构模型。

1 超大直径低壁浅仓的圆环壳结构模型

关于图1所示目前国内水泥生产企业曾大量建成并正在服役的超大直径带扶壁柱与桩基的钢筋混凝土低壁浅仓,经计算分析表明,该仓体由于底部固定,其季节性温度变化引起的扶壁柱竖向弯矩达到7.092×104(kN·m)/m,剪应力达到1.749×107Pa,而仅考虑仓内散料满仓堆载工况下其竖向弯矩为3.83×104(kN·m)/m,剪应力仅2.073×106Pa,由此可见温度变化引起的荷载效应已远超散料满仓时的影响。另外,地震作用引起的水平剪力对该结构也有不可忽视的影响。由于基于挡土墙计算理论,认为贮料会在仓底部产生很大的弯矩和水平剪力,从而导致了变截面扶壁柱和桩基础以及大截面基础环梁的设置,造成了巨大的人力、物力和财力上的消耗。

本文提出的超大直径低壁浅仓圆环壳结构无矩理论模型,其理论依据是圆柱壳无矩理论(即圆柱壳体的薄膜理论),该模型无须桩基,仓壁上下边无须加强环梁和基础环梁(也可按构造要求设置),该圆环壳结构直接位于一光滑的圆形环带状高强度钢筋混凝土地基表面上(图2),壳壁底边相对于圆环带地基表面沿径向可滑动(遭遇地震时具有隔震器效应。实际存在一定的水平摩擦力,其大小取决于壳体底面和圆环带地基表面之间的摩擦系数;例如,可在上部壳体施工前先在预先打磨做光的圆环形地基表面上涂刷脱模剂或润滑剂并覆盖分隔膜片等措施来减小摩擦力),壳体内主要处于无矩内力或薄膜内力状态(即按《规范》所述对于圆形筒仓或浅圆仓,在远离固定端或约束区的仓壁内力,可按无矩理论计算),极大程度地降低了上述其他模型结构和《规范》所述的温度应力和边缘效应,并可将结构受到的地震作用降至最小,能极大程度地节省材料、降低造价和缩短施工工期。

图2 基于圆环壳无矩理论的超大直径低壁浅仓Fig.2 Silo based on annular shell structure with membrane theory

图3所示为农村大量使用的粮囤,由一定宽度的带状编织物向上围绕成图示圆柱形围囤,其下端直接位于地表面上。稻谷等装载后粮囤壁内仅承受环向拉力(这也是该粮囤壁唯一能承受的内力,稻谷对囤壁的法向压力远小于由此引起的囤壁内环向拉力),无任何纵向弯矩(该粮囤的构成方式也无法承受任何弯矩)和边缘效应。囤底部沿地面可滑动不受约束,如有地震引起地面运动,则只是地面相对粮囤作水平运动而粮囤底边因可滑动而不易损坏。

图3 农村篾席编织物围绕成的粮囤Fig.3 Rural bamboo mat woven fabric around grain stock

本文圆环壳结构形式和支撑方式是受图3所示粮囤类型受力性质的启发而提出,图2所示的建立在无矩理论基础上的圆环壳在使用功能上完全等同于图1所示按挡土墙理论计算设计的结构功能,而前者使用的材料、施工工期和建造费用等均远低于后者,因此本文提出的结构模型具有重要的理论意义和广泛的工程应用价值。

2 理论计算与数值分析

本节将对本文提出的圆环壳结构无矩理论模型筒仓在满仓堆载工况下进行无矩内力计算与设计,并利用有限元ABAQUS软件在偏载情况下进行局部弯曲内力校核。该圆环壳贮料浅仓仓壁为钢筋混凝土结构,筒仓内径为80 m,仓壁高13 m,混凝土强度等级为C40,弹性模量E=30 GPa,混凝土密度ρ=2 500 kg/m3,泊松比μ=0.2,仓壁配筋选用HRB400级钢筋。贮料容重γ=1.0×104N/m3,贮料堆载内摩擦角φ=38°,贮料压力荷载采用折算库伦公式Ph=kγs确定,k为主动土压力系数(内摩擦角φ=38°时k=0.238),γ为贮料容重,s为贮料锥体重心到计算截面高度。在进行筒仓设计时仅考虑仓体自重及贮料压力荷载对结构的作用。

2.1 圆环壳筒仓无矩理论计算与设计

圆柱壳的无矩理论平衡微分方程形式如下[8]:

(1)

式中:q1,q2,q3为柱壳所受荷载分别在纵向、环向及法向的分量,本文壳体q1=-ρgt,q2=0,q3=0.238γ(13-α),t为仓壁厚度;FT1,FT2及FT12=FT21分别为纵向拉压力、环向拉压力及平错力。在进行计算时,可先由上述平衡方程第三式求出环向拉力FT2,然后代入第二式对FT12积分(积分常数由边界条件确定,下同),求出平错力FT12,再将FT12代入第一式,对FT1积分,求出纵向拉压力FT1。对上式求解,并将各边界条件代入求解后得到各内力表达式:

FT1=ρgt(α-H)

FT2=0.238γ(H-α)R

FT12=FT21=0

(2)

式中:H为仓体高度。

1) 仓壁厚度设计

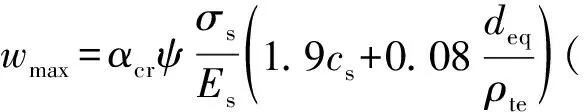
2) 环向配筋计算

将各几何物理参数代入可得环向拉力最大值为FT2max=1 238 kN/m,发生在仓底。仓壁环向受力钢筋按轴心受拉构件计算:FT2max≤fyAs,经计算仓壁内外侧分别按20@90配筋对称布置,保护层厚度30 mm。为了控制仓壁竖向裂缝,可采取在仓壁内沿高度增设适当数量的暗环梁,并沿周向布置适当数量的暗柱等措施来避免壳体严重开裂。

3) 竖向配筋计算

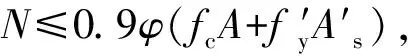
其它配筋及构造措施均可按《钢筋混凝土筒仓设计规范》(GB 50077—2003)要求配置。

2.2 圆环壳浅仓内力有限元计算

以下将利用有限元软件ABAQUS对3.1节所述圆环壳仓体在贮料满仓堆载和局部堆载压力作用下进行有限元计算,检验上述按无矩理论设计的仓体是否符合安全要求。算例中仓体内径80 m,高13 m,变截面壁厚底部厚450 mm,仓顶壁厚250 mm;其中局部堆载(偏载)形式见图4(按堆载半角β为30°、90°及150°三种工况分别进行有限元计算)。

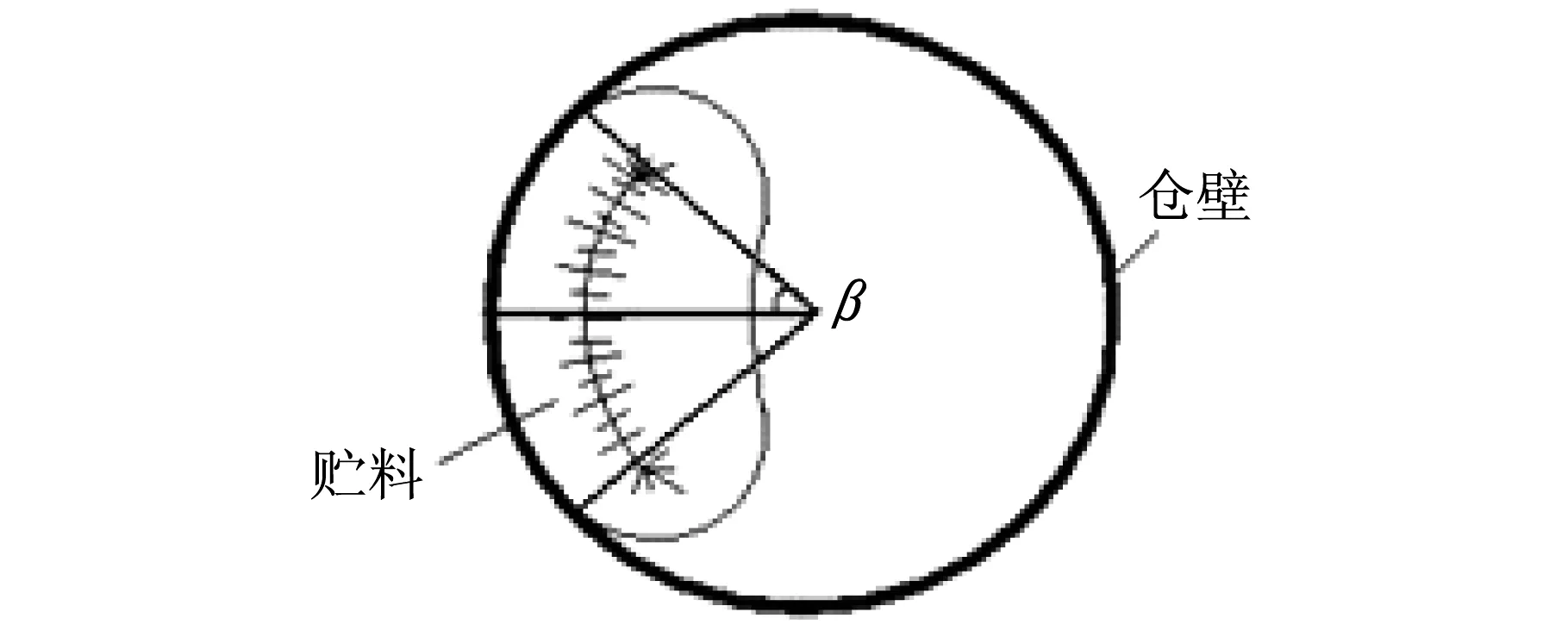
图4 贮料局部堆载形式Fig.4 Storage form at local load

满载和偏载时利用对称性分别取1/4及1/2结构建模分析,采用ABAQUS软件中S4R壳单元,单元尺寸0.2 m×0.2 m,1/4壳体共划分20 475个单元,1/2壳体共划分40 950个单元。

为便于校核对比,列出满仓堆载时的仓壁环向拉应力和竖向压应力沿仓壁分布见图5和图6。从图5应力云图可见满载时仓壁底部最大环向拉应力σ=2.687×106Pa,折算成环向单位长度截面拉力为F拉=1 209 kN/m(本文按无矩理论计算公式得到FT2max=1 238 kN/m)。局部堆载半角为30°的计算结果见图7和图8,可见底部最大环向拉应力为2.65×106Pa;局部堆载半角为90°的计算结果见图9和图10,其底部最大环向拉应力为2.822×106Pa;局部堆载半角为150°的计算结果见图11和图12,其底部最大环向拉应力为2.643×106Pa。由上述三种偏载工况下的内力比较可见,第一种和第三种工况下的最大环向拉应力均小于满载时无矩理论结果,其中第二种工况偏载半角90°较为不利,其底部最大环向拉应力为2.822×106Pa,超过按无矩理论计算最大拉应力2.751×106Pa约2.6%,在允许的5%偏差范围内。因此,可认为本文按圆柱壳无矩理论设计的圆环形浅仓可满足偏载引起的局部抗弯强度校核。壳体内竖向压应力主要是壳体自重引起,而局部堆载会对其略有影响,其计算结果见图8、图10和图12,第一种和第三种工况下的竖向压应力相对略大,为1.951×105Pa,折算成单位宽度壳体轴向压力值为87.79 kN/m,仍远小于仓壁竖向设计承载力,因此按圆环壳无矩理论设计的浅仓可满足偏载引起的竖向抗弯强度校核。

图5 满载时环向拉应力 Fig.5 Circumferential stress at full load

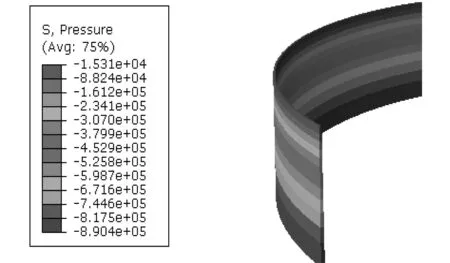
图6 满载时竖向压应力Fig.6 Compressive stress at full load

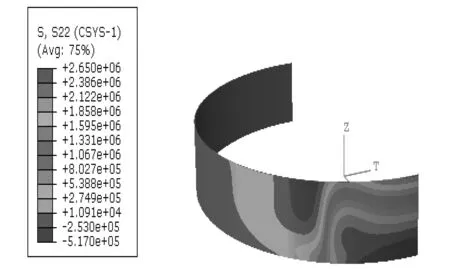
图7 堆载半角30°环向拉应力Fig.7 Circumferential stress at loading angle of 30 degrees

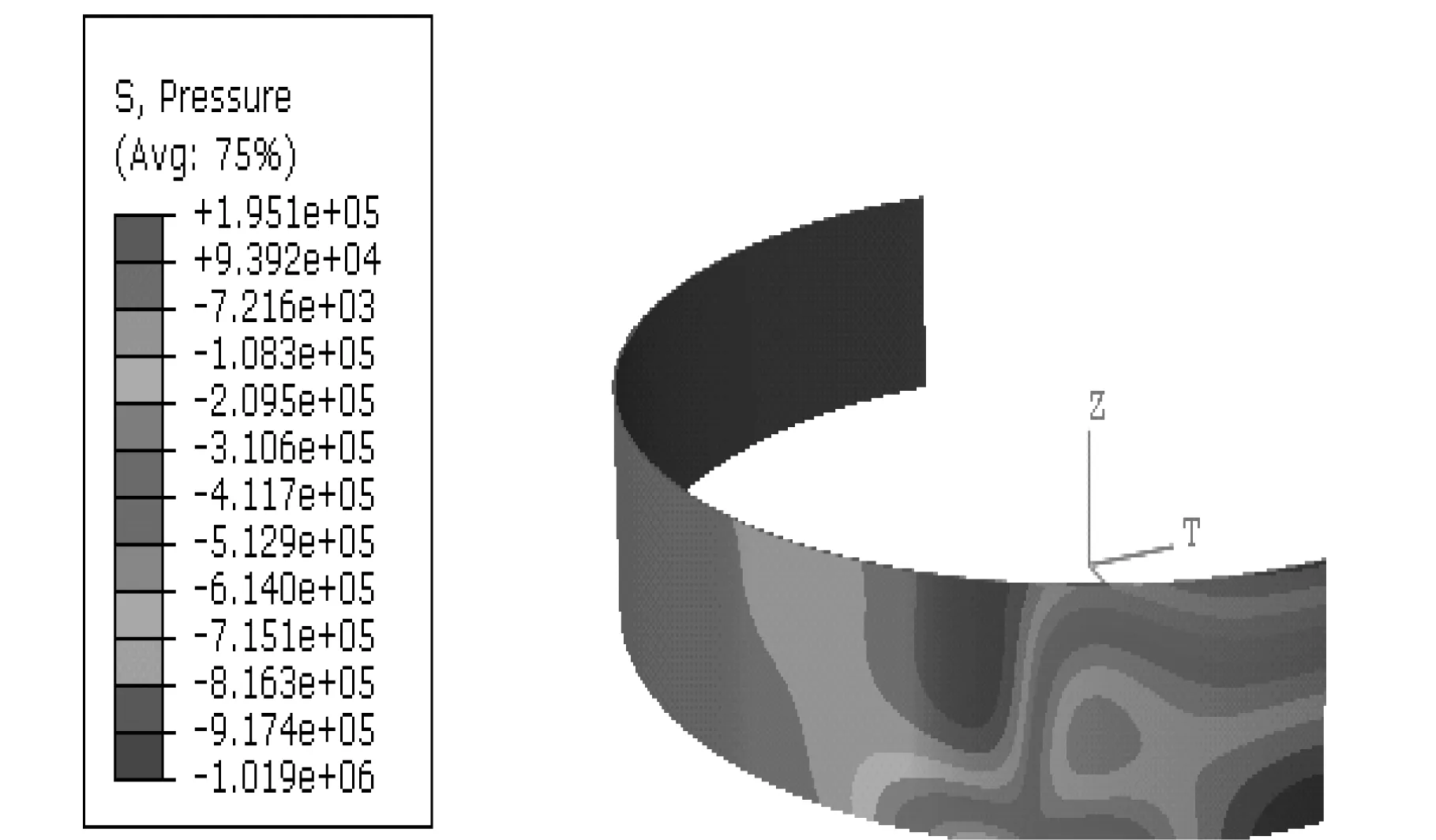
图8 堆载半角30°压应力Fig.8 Compressive stress at loading angle of 30 degrees

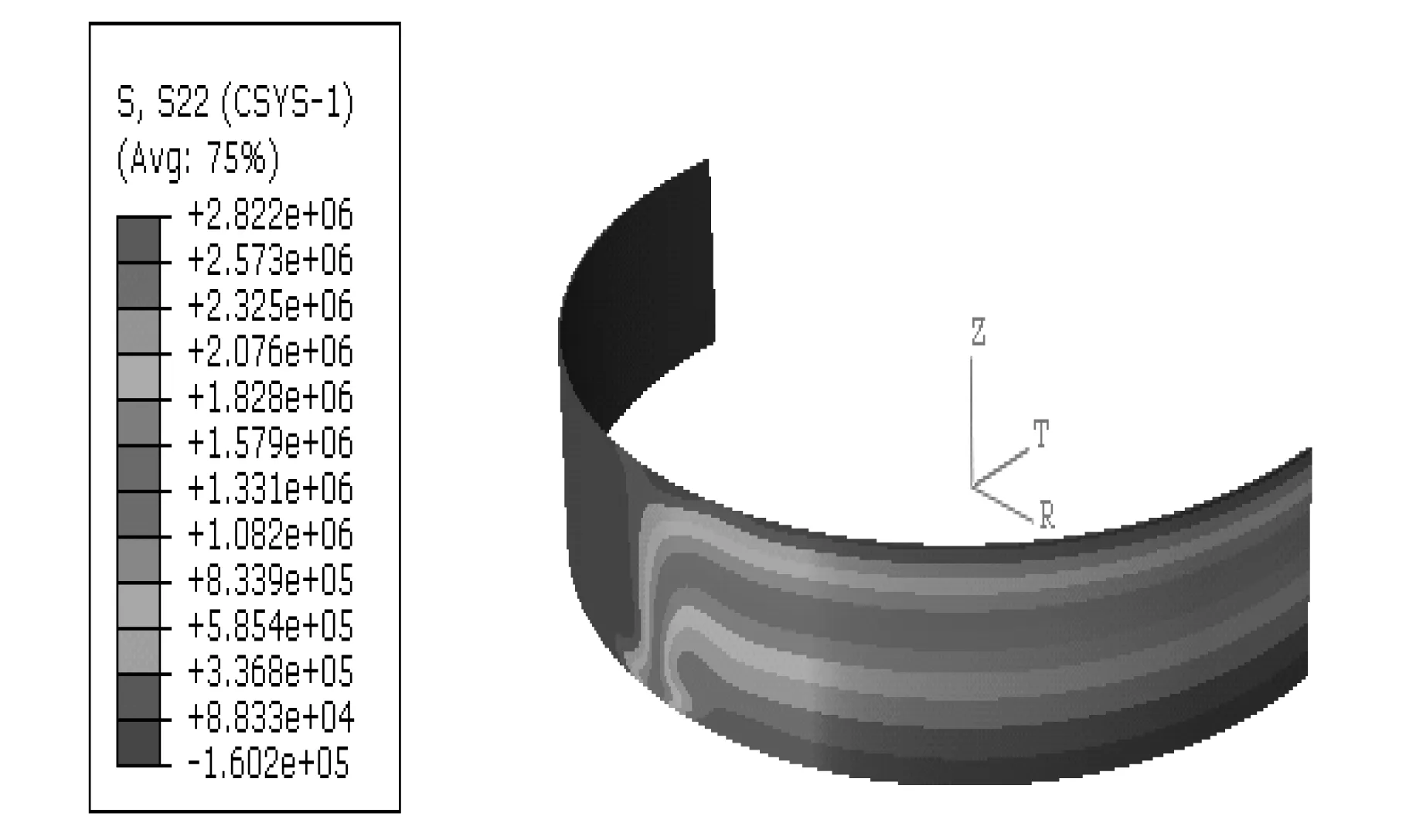
图9 堆载半角90°环向拉应力 Fig.9 Circumferential stress at loading angle of 90 degrees

图10 堆载半角90°压应力Fig.10 Compressive stress at loading angle of 90 degrees

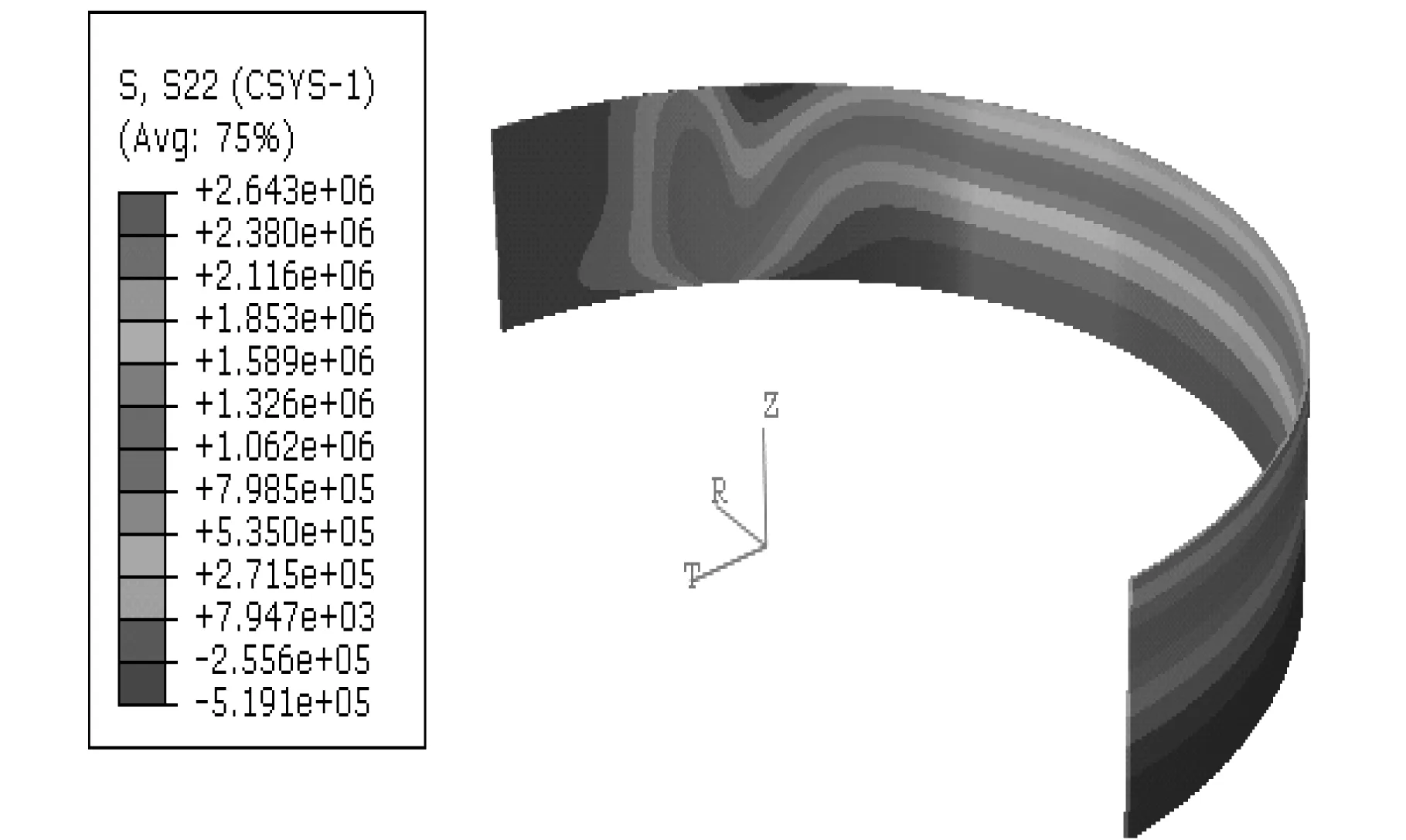
图11 堆载半角150°环向拉应力 Fig.11 Circumferential stress at loading angle of 150 degrees

图12 堆载半角150°压应力Fig.12 Compressive stress at loading angle of 150 degrees

另外,观察图7-图12结果云图可见,上述偏载工况引起的应力仅在堆载边界面附近有所变化,其他区域影响较小。

3 结 论

通过结构计算与理论分析,可得如下结论:

(1) 本文提出的超大直径低壁浅仓圆环壳结构无矩理论模型及其支撑形式理论上是可行的。该圆环壳底部直接位于圆环状平整光滑的钢筋混凝土地基上,且壳底沿径向理论上可滑动(该支撑形式遭遇地震时具有隔震器效应),因此仅需按圆柱壳无矩理论设计与配筋,可将温度应力和边缘效应降至最低,是对现行《规范》的一个重要补充,具有重要的理论意义和广泛的工程应用价值。

(2) 笔者认为,无论圆形筒仓直径是多少,即便对于直径为120 m或更大的巨型浅仓,其结构受力与抗力本质上还是壳体结构,若采用本文提出的圆环壳结构模型及其支撑方式,则只需按无矩理论计算与设计。若沿用挡土墙理论设计,势必造成巨大的人力物力和资源上的浪费,不符合当今建设绿色环保建筑要求。

(3) 建议在按本文结构模型与理论进行超大直径低壁浅圆仓或巨型浅圆仓结构计算与设计时,可按构造要求在仓壁底部、中间一定间隔和顶部等设置适当数量的圆环形暗梁,并可沿竖向布置若干暗柱,以增强仓壁的整体性与抗裂性。