基于PSO算法的CT系统标定模板的优化设计
2018-11-22林勇康艾昕晨王汝传
张 路,林勇康,艾昕晨,沙 超,王汝传
(1.南京邮电大学 计算机学院、软件学院、网络空间安全学院,江苏 南京 210003; 2.南京邮电大学 电子与光学工程学院、微电子学院,江苏 南京 210003)
0 引 言
CT系统,即电子计算机断层扫描,是一种可以利用人体不同组织对X射线吸收率的不同而对人体内部进行成像的仪器[1-2]。此外,CT也可以应用在工程上,工程CT可以对工程对象内部进行成像,完成工程结构检测等任务[3]。
然而,在CT系统安装完成后,系统往往存在误差,需要用已知参数的标定模板来进行误差参数标定,便于进行误差补偿。因此,标定模板的设计往往影响着标定误差参数的精度,进而影响到最后的成像质量。文中提出的基于PSO算法的标定模板设计方案,具有精度高、收敛快等特点,并与爬山法、遗传算法进行了对比。
1 CT系统工作原理
一种常见的CT系统如图1所示。系统工作时,样品以及托盘静止不动,512个等间距的“光源-探测器单元组”绕托盘某固定旋转中心逆时针旋转180次。由于旋转误差的存在,不一定是等间距旋转。经过处理后,计算机得到180组接收信息,每组接收信息包含512个探测器的探测数值,即可根据探测器信息结合标定的参数还原样品截面图。CT系统的参数标定是指标定安装完成后的旋转中心点的坐标,探测器单元的间距,以及CT系统旋转的180个方向角。
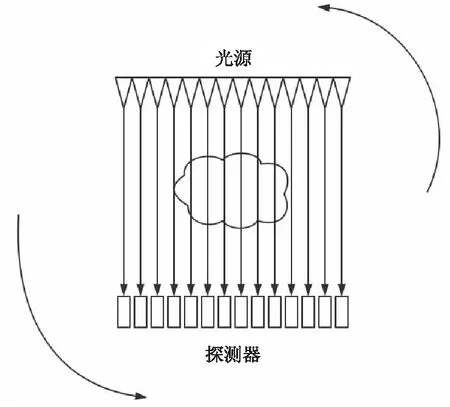
图1 CT系统工作原理
为了提高标定的精度和稳定性,需要对模板进行最优化设计。模板的设计围绕以下3个目标进行:标定精度尽量高;单个探测器的接收信息方差尽量大;探测器的利用率尽量高。
其中,“单个探测器的接收信息方差尽量大”这个目标会充分利用探测器的量程,以对不同材质起到更好的区分度。但是,此目标将导致模板呈现直杆形状,因为直杆形状下的模板能让单个探测器的接收信息从0变化到最大值。
而“探测器的利用率尽量高”这个目标,会充分利用探测器资源。但是,此目标将导致模板呈现半径较大的圆形。因为半径大的圆形在任何角度下都能被更多的探测器探测到。
综上所述,在各个目标的制约与均衡下,最终的模板主体形状会是一个介于圆与直杆之间的形状,即椭圆形。此外,为了能够更加便捷地测定探测器间距,并能够使模板产生不对称性,以增大各个方向的接收信息区别,在椭圆右侧引入一个圆。
故最终的标定模板为一个椭圆与一个圆构成的图形,假定圆位于椭圆右侧。在标定模板的设计方案中,需要求解的参数有椭圆的离心率e,长轴长度a,圆的半径r,圆心和椭圆中心的距离d。设定模板为均匀的单一材质,吸收率μ为1。
2 多目标规划模型的建立
为了求解出最优的标定模板,针对上文中的待定参数,建立多目标规划模型,分别确定目标函数和约束条件,过程如下所述。
2.1 目标函数的建立
2.1.1 目标函数一:标定精度尽量高
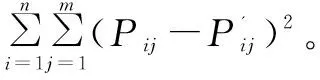
由于接收信息经过了增益等处理,结合Beer-lambert定律[4],理论值可以通过下式计算。
(1)
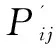
2.1.2 目标函数二:单个探测器接收信息方差尽量大
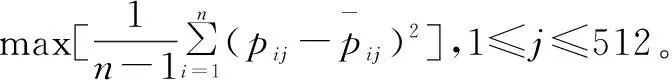
2.1.3 目标函数三:探测器的利用率尽量高
2.1.4 目标函数的转化
对于三个目标函数,求解的难度相对较大,因此,在保证目标不变的情况下,可对目标函数进行一定的改进。
目标函数一可转化为:max(d-b-r)2。目标使圆与椭圆间隔尽可能大,根据探测器间距测量方法,能提高探测器间隔的标定精度。
目标函数二可转化为:maxe。此目标使得椭圆尽可能扁平,从而使得单个探测器接收信息方差尽可能大。
目标函数三可转化为:maxa2+b2,此目标使得椭圆尽可能大,从而提高探测器利用率。其中,a为椭圆形模板的半长轴,b为椭圆的半短轴。
其示意图如图2所示。
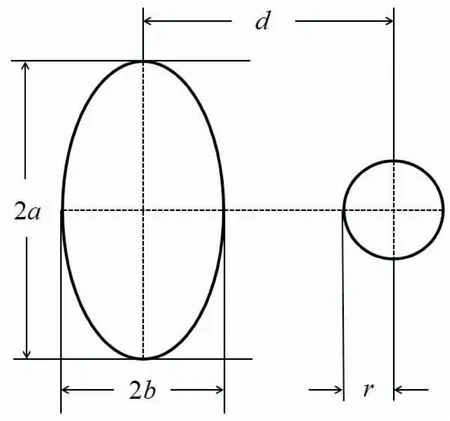
图2 待求解模板示意图
考虑到所求的目标函数都是要求最大值,因此首先考虑相加。但是因为数量级上有差异,首先要将其进行标准化[5],建立一个目标函数F。将上述三个目标函数分别记作F1,F2,F3,则最终的目标函数为:
(2)
2.2 约束条件的确定
约束条件一:椭圆长轴长度与离心率范围的约束。一方面,椭圆要限定在托盘内。文中的系统托盘宽度为100 mm。另一方面,椭圆不能与圆相交,由此得到如下两个约束关系:
(3)
约束条件二:圆的半径范围约束。圆的半径范围一方面与椭圆离心率有关;另一方面,半径和圆与椭圆中间距离也限定了圆不能超出托盘区域,关系式如下:
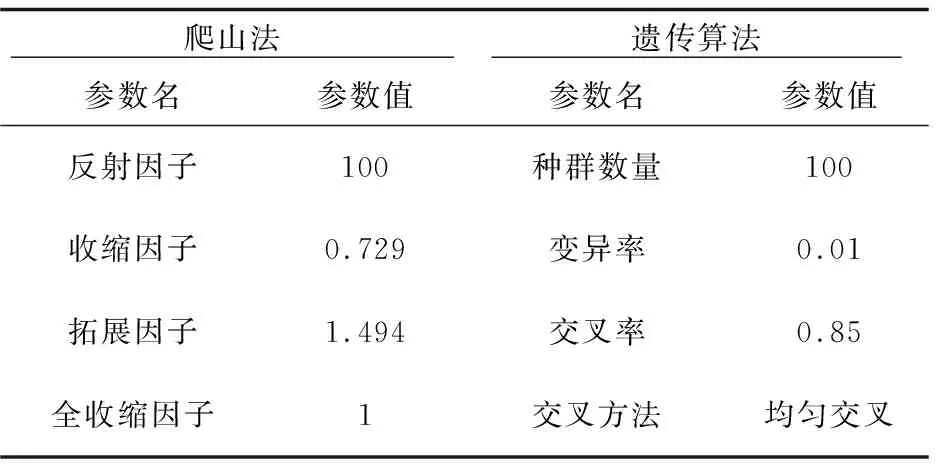
0 (4) 约束条件三:圆与椭圆相对位置关系的约束。为了能够更加方便地测定探测器间距,要保持圆和椭圆之间有一定的间距,关系式如下: (5) 根据新设计的模块信息,可采用对参数遍历的方式来达到多目标规划的最优解。然而,考虑到需要对椭圆的离心率e,椭圆的长轴长度a,圆的半径r、椭圆中心和圆心的间距d,分别进行遍历,计算量繁重且结果不精确。故根据收敛速度及求解精度的需要,采用PSO算法[6-10]对模型进行求解。 PSO算法,即粒子群优化算法,是由Eberhart和Kennedy基于群鸟觅食行为提出。在粒子群算法中,每个粒子都被当成一只鸟。在群鸟觅食的过程中,每只鸟的初始位置和飞翔方向都是随机的。每只鸟都不知道食物的具体位置。但是,随着时间的推移,这些鸟通过相互学习、信息共享和不断积累觅食的经验,自发组织积聚成一个群落,并朝着食物前进。迭代终止的条件一般为目前搜索的最优位置满足目标函数的最小容许误差,或者达到了最大迭代次数。 在本例中,PSO算法的具体步骤如下: 步骤1:由于需要对椭圆的离心率e,椭圆的长轴长度a以及圆的半径r、椭圆中心和圆心的间距d进行遍历求解,因此,首先确定一个四维粒子(a,e,r,d),根据已经确定的约束条件,在范围内对四维粒子进行赋值。 (6) 步骤2:在已经确定的约束条件下,进行第一次选取。为了能够得到全局最优解,需要先设置100个粒子,粒子按照粒子运动规律在全局范围内演变。在满足最优化目标的条件下,从粒子群中选取较小的(a,e,r,d)作为下一次选取的上限:amax,emax,rmax,dmax。 步骤3:同理,在满足最优化目标的条件下,从粒子群中选取较大的(a,e,r,d)作为下一次选取的下限:amin,emin,rmin,dmin。 步骤4:在已经确定的上下限范围内进行下一次选取。 (7) 步骤5:设定迭代次数。经过测试,本例中的PSO算法大部分在31~73次迭代之后达到收敛条件。为了兼备结果的精确性和速度,选定最大迭代次数为100次。 在托盘尺寸为100 mm×100 mm,探测器为512组,旋转180个角度的情况下,对表1中PSO算法的求解参数进行求解。 表1 PSO算法参数值 借助MATLAB的粒子群工具箱,求得标定模板的各项参数值,如表2所示,此时的目标函数值为2.086 2。 表2 标定模板的各项参数 为了检测PSO算法与其他优化算法在求解本问题上的优劣,分别采用爬山法[11-12]和遗传算法[13-15]进行求解。 爬山法是一种求解局部最优解效果较好的算法。通过不断与邻居节点的函数值进行比较,如果邻居节点函数值较大,则用邻居节点代替当前节点,从而寻求到最优解。若初值选取的不恰当,爬山法往往找到的是局部最优解。 遗传算法是基于达尔文进化论产生的一种随机搜索算法,通过模拟自然界生物进化过程寻找最优解。包含复制、交叉、变异三种算子。对非线性问题有良好效果。 爬山算法和遗传算法的参数如表3所示。 表3 爬山算法与遗传算法求解参数 爬山法 遗传算法 参数名参数值参数名参数值反射因子100种群数量100收缩因子0.729变异率0.01拓展因子1.494交叉率0.85全收缩因子1交叉方法均匀交叉 在MATLAB R2017b下,经过求解,得到的迭代搜索对比如图3所示。 图3 不同算法迭代搜索图 由图可以看出,在本例中,爬山法容易陷入局部最优解的状况,在多次测试中,只有少数几例由于随机初值选取在全局最优解附近,使得爬山法取得了全局最优解,其他大部分情况均陷入了局部最优解。而本例中存在4个维度的搜索,遗传算法在高维问题的收敛速度较慢甚至很难收敛。 提出了一种基于PSO算法的标定模板的设计方案。首先根据设计目标确定标定模板大致形状,然后根据相关目标与约束条件建立多目标规划模型,最后采用PSO算法求解出模板的参数,得到了在指定情况下的最优化模板设计方案。与爬山法、遗传算法的对比结果证明了PSO算法在本例中的优越性。 但是,在运行过程中,PSO算法同样存在一些问题,例如求解参数的设置对最终结果影响很大,局部搜索能力较差,结果不稳定等。因此,如何降低对参数的依赖性,提高结果的稳定性和局部搜索能力,是下一步的研究方向。3 基于PSO算法的优化求解
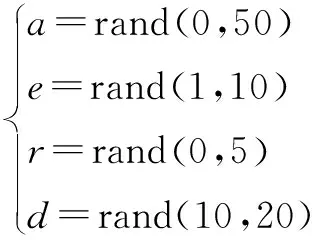


4 不同算法对比

5 结束语
