基于重心点转移的St-DBSCAN改进算法
2018-11-22姚绍文
刘 勇,何 婧,姚绍文,向 毅,张 浩
(云南大学 国家示范性软件学院,云南 昆明 650500)
0 引 言
聚类(clustering)是数据统计分析的重要组成部分。对实际数据的聚类需要聚类算法根据不同的方法进行聚类分析。迄今为止,已经提出了大量的聚类算法,包括OPTICS[1]、DENCLUE[2]、DBSCAN[3]、GCHL[4]、BIRCH[5]、K-MEDOIDS[6]和Clara[7]等,其中DBSCAN算法是一种常用的基于密度的聚类算法。
DBSCAN在生产中的应用十分广泛。例如,利用DBSCAN算法对某段时间的居民出行数据进行聚类,能有效预测出当地可能出现的交通堵塞的地点,为公民出行提供良好的建议;利用DBSAN算法对台风出现地点进行聚类,能有效地预测出台风的走向。从DBSACN算法提出以来,众多学者对其提出了改进,如IDBSCAN[8]、VDBSCAN[9]、OVDBSCAN[10]、DP-DBSCAN[11]、SA-DBSCAN[12]、Greedy DBSCAN[13]等,这些算法概括来讲主要是从聚类方式、聚类参数、空间点区域划分等方面进行的改进。
Derya Birant[14]在DBSCAN算法的基础上,通过增加非空间距离值参数,使DBSCAN算法能够对含有非空间距离值的空间数据进行聚类。但是自St-DBSCAN算法提出以来,至今尚未有相关文献对其进行改进。但St-DBSCAN算法在空间数据分布式出现数据倾斜时,会出现聚类时间过长和聚类效果差的问题。基于上述不足,文中通过求邻近点重心转移的方法对其进行改进。改进St-DBSCAN算法对空点分布出现密度倾斜时,通过寻找邻近点的重心能更快地找到邻近点分布最多的区域,然后再以重心点为核心点进行聚类,使形成的簇更加紧密,从而提高算法的聚类效果。
1 St-DBSCAN算法概述
St-DBSCAN算法中有三个参数:Minpts、Eps、Δt。其中Minpts表示形成簇的最小点个数,Eps表示形成簇的时空点距离,Δt表示形成簇的最大时间。St-DBSCAN算法的基本思想是:通过循环判断时空核心对象c以Eps为半径,Δt时间差内点的个数是否大于等于Minpts,如果大于则形成簇,反之则对下一个时空对象进行聚类,直到所有的时空对象都归在某个簇中,或被标记为时空孤立点,则聚类结束。
但是,如果选取的核心点偏离空间点分布的密度集中区域,St-DBSCAN算法不能很好地解决密度倾斜问题,同时由于St-DBSCAN算法需要对所有的空间点进行遍历,导致运行时间较长。
2 改进的St-DBSCAN算法设计
改进的St-DBSCAN算法通过对空间点分布出现的三种密度倾斜情形,采用求取空间点密度重心的方法获得周围空间点密度分布的重心,然后根据不同的密度倾斜,给出不同的改进方案,对空间点进行聚类。
2.1 相关概念
定义1(邻近重心点):在以核心点为圆心,半径为Eps的圆域内所有邻近点的重心点。
邻近重心点P(x,y)的坐标与所有邻近点的分布有关,具体的坐标计算如下:
(1)
(2)
其中,k表示邻近点个数;pix表示任一邻近点的x轴坐标;piy表示任一邻近点的y轴坐标。

算法中采用的是欧氏距离,因此重心点O1与核心点L1的距离表示为:
(3)
其中,px表示邻近点的x轴坐标;py表示邻近点的y轴坐标。
通过式4可以计算重心点偏离∂。
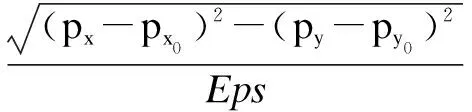
(4)
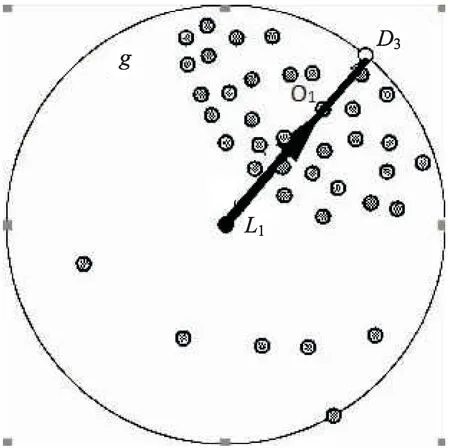
图1 重心点偏离
定义3(密度距离差,ΔDensity_distance):在任意的簇中,任意一点p的簇内最小距离desity_distance_min(p)与该点的簇内最大距离desity_distance_max(p)的差值,称为该点的密度距离差,即ΔDensity_distance(p),其数学定义为:desity_distance_max(p)=MAX{dist(p,q)|q∈D∧dist(p,q)≤Eps},desity_distance_min(p)=MIN{dist (p,q)|q∈D∧dist(p,q)≤Eps}。
对于任意点p的ΔDensity_distance计算如下:
ΔDensity_distance=density_distance_max(p)-
density_distance_min(p)
(5)
定义4(簇聚合度):对于簇C密度因子的计算公式如下:
(6)
簇聚合度反映了簇的稠密程度。由其定义可知,任意簇C的簇聚合度在(0,+∞)的区间内,当簇C的簇聚合度越接近0时,簇C越松散,反之当簇C的簇聚合度越大,则簇C越紧密。
2.2 算法改进
2.2.1 重心点转移的理论推导
引理1:邻近重心点与核心点的距离一定在以核心点为圆心,Eps为半径的圆域内。
假设核心点为P(x0,y0),核心点p有n个邻近点,邻近点{p1,p2,…,pn}坐标分别为(x0,y0),(x1,y1),…,(xn,yn),点h为点p的邻近重心点,设点h的坐标为(px,py)。
证明:
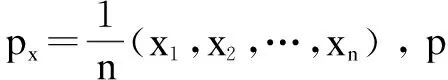
p1,p2,…,pn是核心点p的邻近点,有:
对上式求和可得:
邻近重心点与核心点p的距离为:

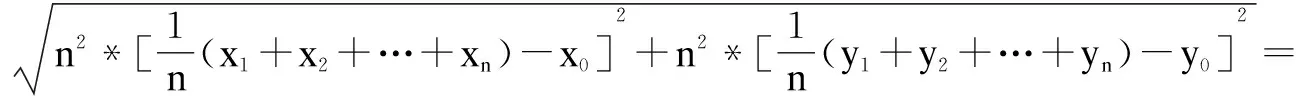
因为
令:
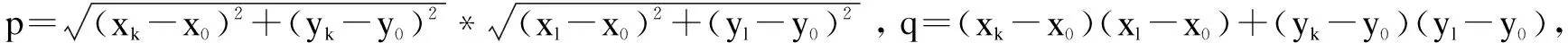
故:
由此得证。
引理2:当邻近点出现密度倾斜时,邻近重心点一定会偏离聚类点。
证明:由式1和式2可得,重心点G(px,py)的坐标点的表达式为:
(7)
(8)
当邻近点某个区域的点比较集中时,设该区域的点为{p1,p2,…,pk},区域点的个数为k,则该区域的重心点表达式为:
(9)
(10)
由此可得:
(11)
(12)
对于重心点坐标公式,可以整理成:
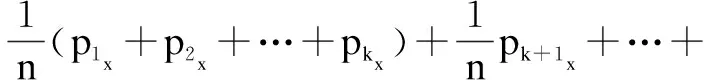
pk}∉P)
(13)

pk}∉P)
(14)
将式11、式12带入式13、式14可得:
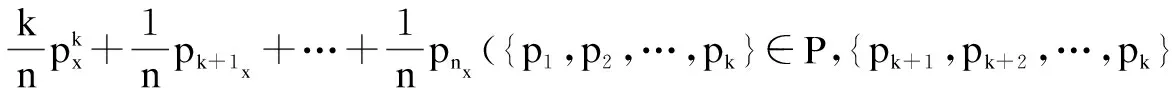
(15)
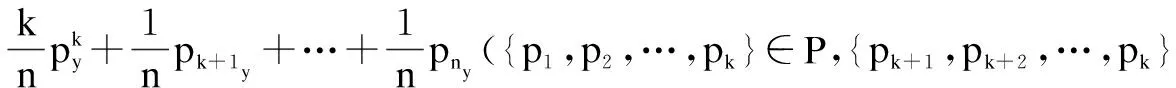
(16)
由式15和式16可知,如果k无限接近于n,重心点坐标将接近于该区内重心点的坐标,如果该区域内的点都偏离于聚类点时,则邻近点偏离聚类点。因此在密度倾斜时,邻近点的重心将偏离聚类点。
2.2.2 核心点重心密度转移
当空间对象在某一个区域比较集中时,会出现密度倾斜的问题。通过对大量的空间对象分布的分析和总结,得出空间对象出现数据倾斜有核心点密度倾斜、边界点密度倾斜和噪声点密度倾斜三种情形。
1.密度倾斜出现的情形。
(1)某个空间数据点符合核心点条件,但是该核心点的邻近点普遍集中于偏离核心点的某一个区域(是否普遍集中可以通过邻近点的重心点偏移核心点的程度决定),称这样的密度倾斜为核心点密度倾斜。
(2)某个空间数据点与邻近点符合时间属性条件,但是邻近点的个数小于Eps,称这样的密度倾斜为边界点密度倾斜。
核心点密度倾斜和边界点密度倾斜统称为同类密度倾斜,因为核心点密度倾斜和边界点密度倾斜中的核心点在时间属性上符合聚类条件,只是在邻近点个数上有所不同。
(3)某个空间数据点与邻近点不符合时间属性条件,称这样的密度倾斜为噪声点密度倾斜。
2.密度倾斜的解决方案。
(1)密度倾斜的判定。
根据式4可知,重心点偏离能反映邻近重心点偏离核心点的程度。如果重心点偏离∂在区间[0,0.5]内,表示重心点靠拢于核心点。反之如果重心点离心率∂p在[0.5,1]内,则表示重心点偏离于核心点,出现了密度倾斜的问题。根据引理1和引理2可知,邻近点重心转移是解决密度倾斜的有效方法。
(2)解决方案。
·核心点密度倾斜解决方案。
图2是核心点密度倾斜情形。图中原本的核心点是A4,但是核心点A4的邻近点明显向图中的右上角倾斜。对于该问题,可以求邻近点的重心点(图2中的G3点),然后再以重心点为聚类点,对空间数据进行聚类。
·边界点密度倾斜解决方案。
图3是边界点密度倾斜情形。图中原本的聚类点是A5,但是A5的邻近点明显向图中的右下角倾斜。对于该问题,可以求邻近点的重心点(图3中的E4点),然后再以重心点E4为聚类点,如果重心点E4的邻近点小于参数minpt,则将所有的点标记为噪声点。反之,则按照核心点密度倾斜方案对空间数据进行聚类。
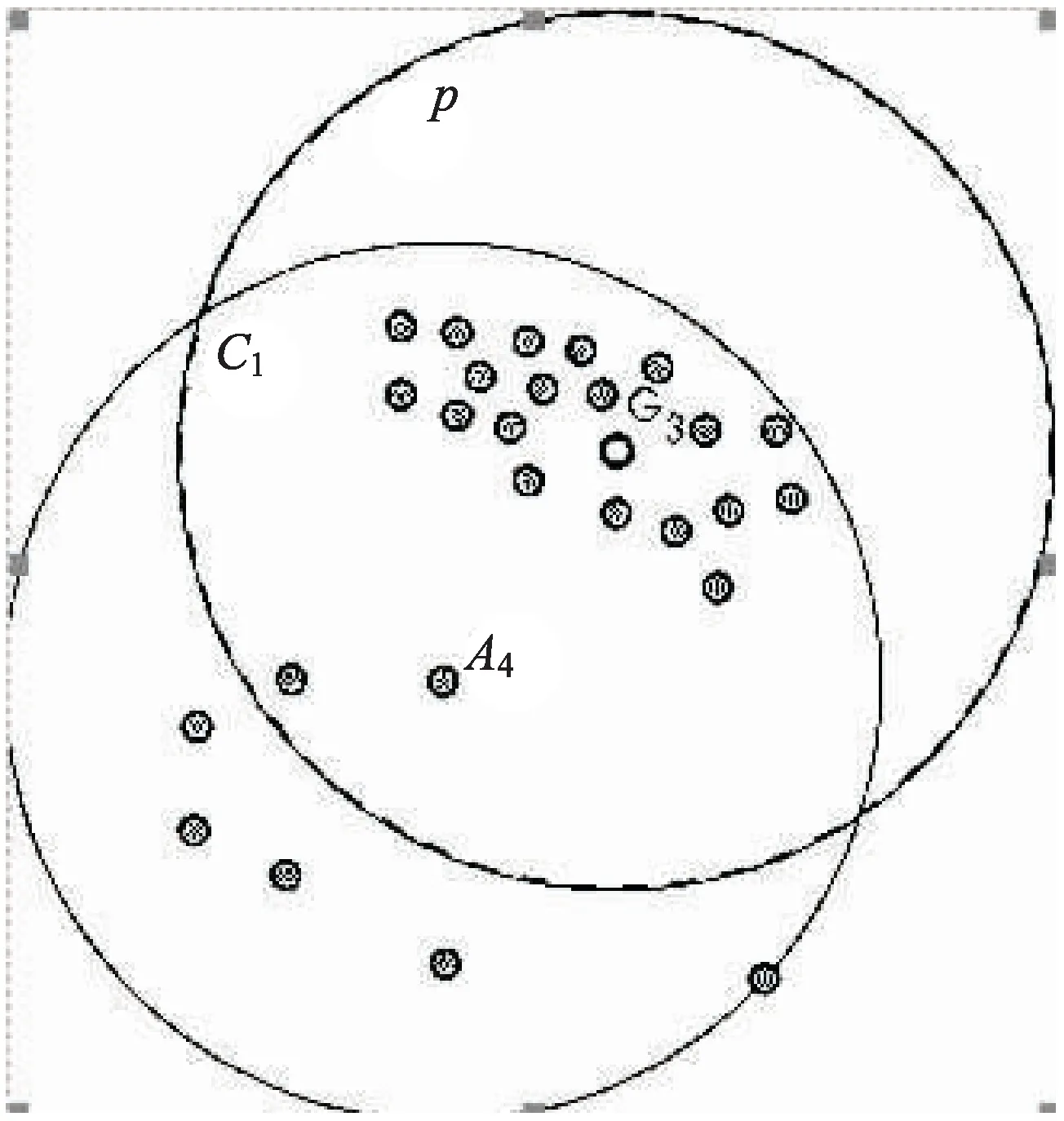
图2 核心点密度倾斜解决方案
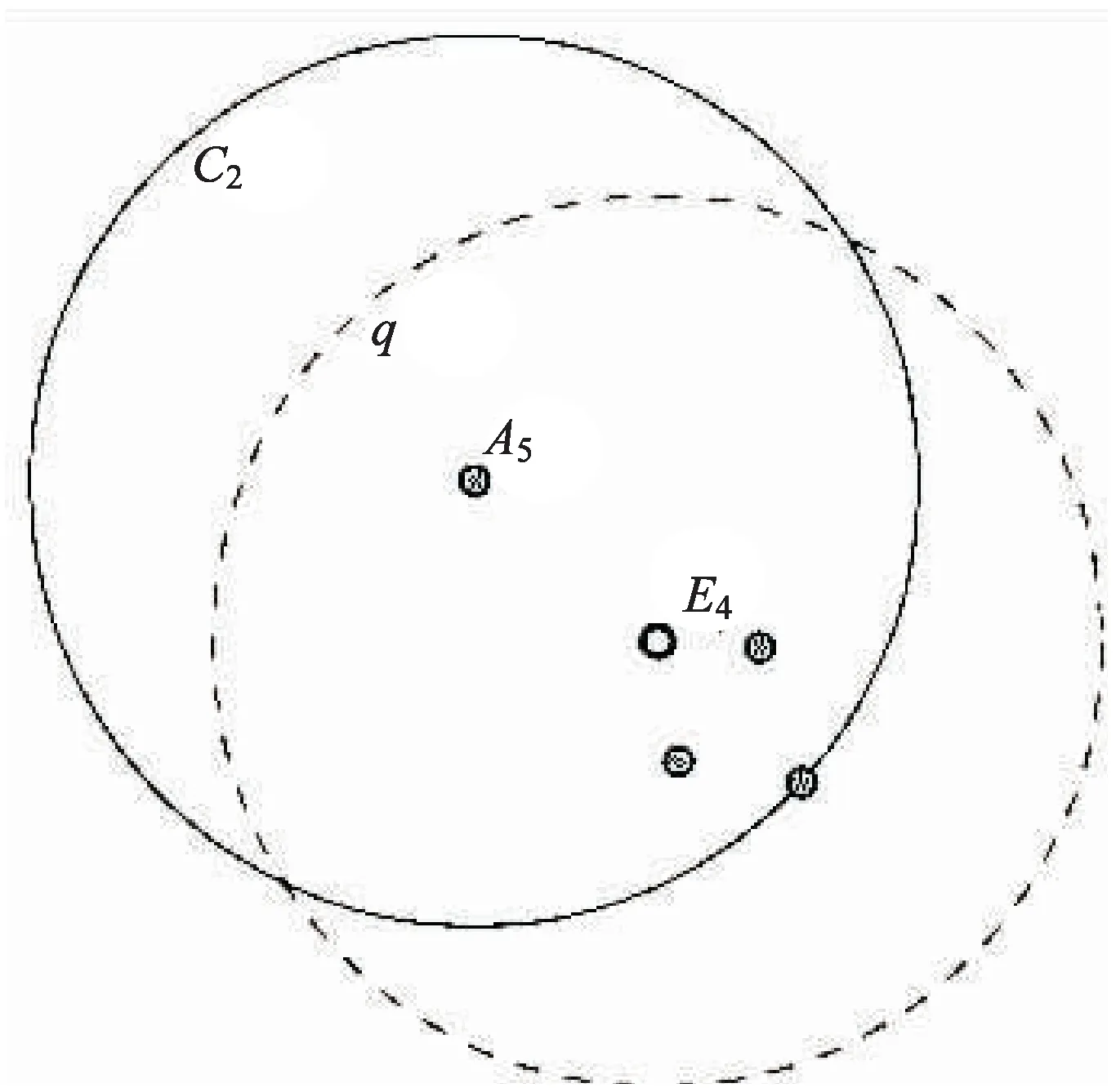
图3 边界点密度倾斜解决方案
·噪声点密度倾斜解决方案。
图4是噪声点倾斜情形。图中原本的核心点是A4,但是A4与邻近点明显不属于同一时间维度,不是同一类。对于该问题,将点A4标记为噪声点。
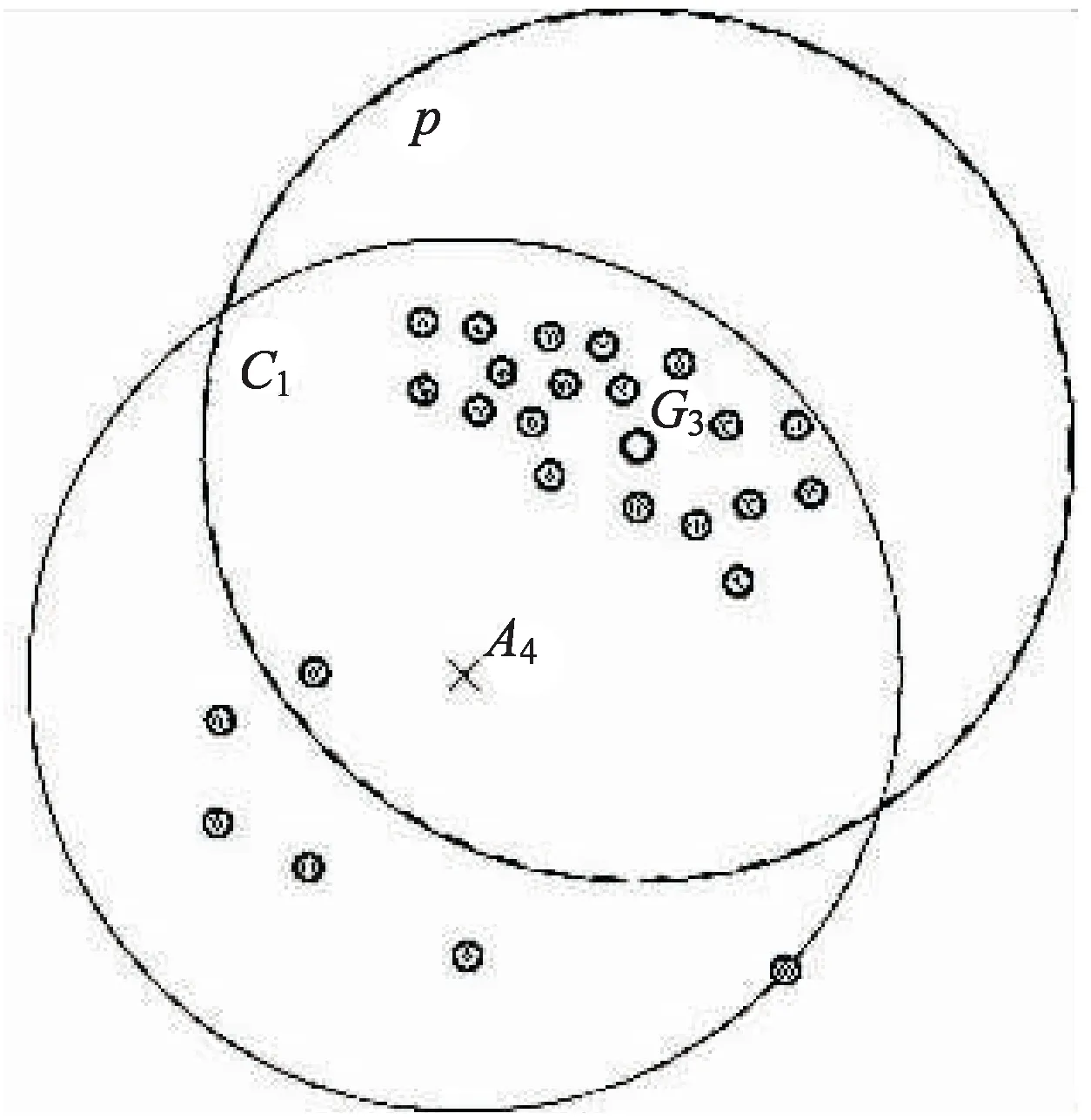
图4 噪声点密度倾斜解决方案
2.2.3 重心点密度转移的St-DBSCAN算法描述
基于上述理论推导和改进方案,改进St-DBSCAN算法的具体执行步骤如下:
步骤1:从任意的空间对象集合D={p1,p2,…,pn}取出一点p,把时空对象当作一个核心对象o。
步骤2:在空间数据集中搜寻满足式17的空间对象,并计算邻近点的个数num是否大于阈值Minpts。如果大于,执行步骤4;反之执行步骤3。
timeCondition(pi,pi+1)≤Δt,∀pi,∀pi+1∈Lm
(17)
步骤3:通过式3和式4计算出重心点位置和重心点偏离空间对象p的偏离程度l,计算出空间对象p的邻近点个数num,根据num与Minpts和l的大小来判断空间对象分布是否出现密度倾斜和出现的是什么类型的密度倾斜,根据不同的数据类型采用不同的密度倾斜解决方案。
步骤4:如果没有出现密度倾斜且邻近点的个数大于等于Minpts,则在邻近点中搜寻每个没有被访问的点的邻近点,如果邻近点的邻近点个数小于Minpts则标记该点为border点。如果该点的邻近点的邻近点个数大于等于Minpts,则标记该点为核心点,并把邻近点的邻近点以及邻近点本身添加到核心点所在簇中。
步骤5:如果没有出现密度倾斜且邻近点的个数小于Minpts,则将该点标记为噪声点。
步骤6:循环执行步骤2~6,直到对于∀Lm,Ln⊂STD,m≠n满足式18和式19,则聚类结束。
Lm∩Ln=∅
(18)
(19)
基于重心点转移的St-DBSCAN算法伪代码如下:
改进后ST_DBSCAN(D,Eps1,Eps2,Minpts,Δt)
输入:数据对象集D={o1,o2,…,on};最大的地理空间距离值Eps1;最大的非空间距离值Eps2;Eps1和Eps2距离内的空间点个数Minpts;形成非空间阈值的阈值Δt,这里是指时间维度
输出:空间点对象聚类簇C={C1,C2,…,Ck}
(1)for each pointpin datasetD
(2)ifpis visited
(3)continue next point
(4)markpas visited
(5)NeighborPts=regionQuerybyTime(p,Δt,Eps2)
(6)/*如果邻近点的个数小于Minpts,将p和p点的邻近标记为噪声点*/
(7)if size of(NeighborPts) (8)markpas NOISE (9)mark NeighborPts as Noise (10)/*求得p点的重心点*/ (11)gravityPoint=getgravity(p,NeighborPts) (12)/*如果重心点偏离聚类点,则以重心点为聚类点对空间数据进行聚类*/ (13)else if distRate(p,gravityPoint)≥0.5 (14)C=next cluster (15)NeighborPts=regionQuery(gravityPoint,Eps1) (16)If size of(NeighborPts) (17)Add NeighborPts toC (18)Make NeighborPts as border (19)Continue next cycle (20)else (21)gravityPoint=getgravity(p,NeighborPts) (22)Continue next cycle (23)expandCluster(gravityPoint,NeighborPts,C,Eps1,Minpts) (24)/*如果重心点不偏离聚类点,则以点p为聚类点,对空间数据进行聚类*/ (25)else if distRate(p,gravityPoint)<0.5 (26)C=next cluster (27)expandCluster(p,NeighborPts,C,Eps1,Minpts) (28)End for End Algorithm 以昆明市出租车GPS数据为实验数据,在Intel Core Duo T9900 3.06 GHz,4核心8线程CPU,内存8 GB的HP台式电脑上运行了改进St-DBSCAN算法与St-DBSCAN算法,并统计了两种算法的运行时间和聚类簇的密度因子。具体的实验数据例样及字段说明如表1所示。 表1 交通信息字段及字段样例 在参数Minpt=50,Maxtime=500 000 ms,Eps=70 m下,选取的数据集条数从500到50 000的运行耗时情况如图5所示。 从图5中可以看出,随着数据集的增大,改进后算法的运行时间与改进前算法的运行时间不断增大,但是改进后算法的运行时间总是少于改进前的算法,其主要原因是改进后算法首先通过时间维度,将不同时间的空间点划分成不同的区域,通过外层循环减少了对空间对象的聚类操作,从而减少了算法的运行时间,提高了算法的时间性能。 图5 算法执行时间对比 为了验证改进后St-DBSCAN与改进前St-DBSCAN的聚类效果,在参数为Minpt=100,Maxtime=50 000 000 ms,Eps=1 000 m下,分别计算空间对象数量在10 000和20 000条件下,6个不同数据集下簇的平均聚合度。具体的实验结果如图6和7所示。 图6 数据集为20 000时算法的簇的聚拢因子 图7 数据集为10 000时算法的聚合度 如图6和图7所示,在数据集数据条数为10 000和20 000时,改进后算法的聚合度大于改进前算法的聚合度,说明改进后算法提高了簇的聚类效果,其原因是改进后算法能通过重心点转移的方式解决空间点分布密度倾斜的问题。 综上,改进后St-DBSCAN算法在算法执行时间和聚类效果上都优于改进前St-DBSCAN算法,因此通过重心转移的方式改进St-DBSCAN算法切实可行。 采用核心点密度转移的方法解决了空间点分布密度倾斜的问题。实验结果表明,改进的St-DBSCAN算法在时间性能和聚类结果中的簇的密度因子都比St-DBSCAN算法有一定程度的提高。但是,对St-DBSAN算法的改进空间依然很大,例如如何通过选取更好的参数进一步提高St-DBSCAN算法的聚类结果,非空间属性与空间属性如何采取合适的聚类策略以提高St-DBSCAN的聚类效果,等等,这些都有待进一步研究。3 实验结果与分析
3.1 实验数据
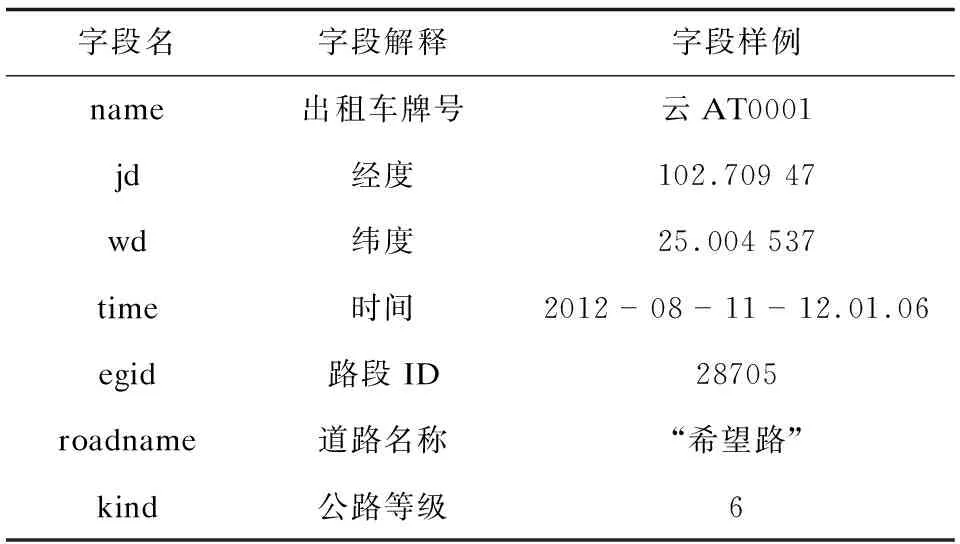
3.2 算法时间性能的对比
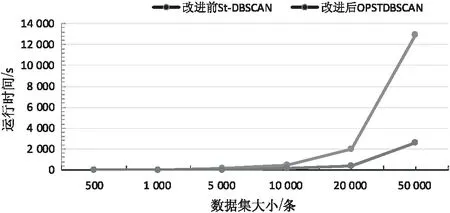
3.3 算法聚类效果的对比
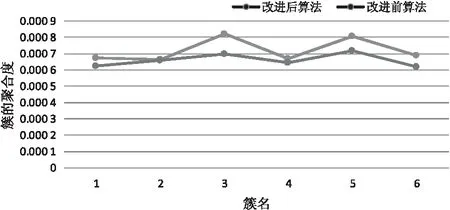
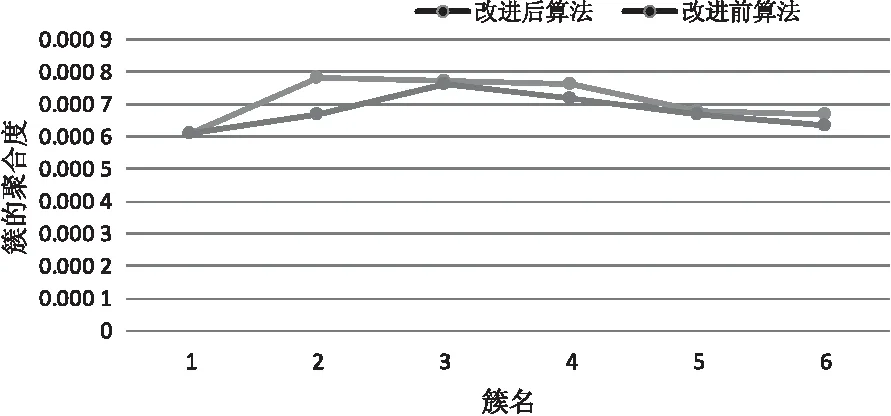
4 结束语
