各向异性球颗粒的古斯-汉森位移

2018-11-21陈久恺朱雯琦高东梁

苏州科技大学学报(自然科学版) 2018年4期

陈久恺，朱雯琦，高东梁，高雷

（苏州大学物理科学与技术学院，江苏苏州 215006）

在几何光学中，当一束光从光密介质n1入射到光疏介质n2，且入射角大于全反射临界角θc=n2/n1时，反射光线在两种介质的界面会发生全反射现象，即入射光全部反射到光密介质中。人们通常认为反射光线和入射光线在界面上是同一点，只是反射光产生了相移。然而实际上发生全反射时光与界面相互作用，会使反射光相对几何光学中的反射光有一段位移，这个位移就是古斯-汉森（GH）位移[1]。古斯-汉森（GH）效应[2-3]自发现以来就引起了人们广泛的兴趣。到目前为止，人们已经研究了各种特殊材料和结构中的GH位移，这些特殊材料和结构包括左手材料[4-5]、光学薄膜[6]、伴有表面等离子激发的金属[7]和一些吸收媒质[8-9]等。GH位移在集成光学系统中应用极为广泛，如光波导、近场扫描光学显微镜等结构[10]。古斯-汉森效应还延伸到了其他物理领域：如声学、量子力学、非线性光学等[11-12]。近年来，各向异性特异材料中的GH位移也引起了人们很大的研究兴趣[13-15]，各向异性材料是指材料的物理、化学等性质依赖于方向，在不同的方向上有所变化。各向异性材料可有负的介电常数和负的磁导率，具有一些与正折射材料不同的电磁性质。在各向异性特异材料里面，可以在部分方向实现负的介电常数或负的磁导率，这比用各向同性特异材料实现这一性质容易得多，而且更有现实意义。近零材料也属于特异材料中的一种，它是指材料的介电常数或磁导率非常小，甚至可以忽略，因此，材料的光学特性都会相应发生变化，普通近零材料中的GH位移已经有学者做了深入分析[16]。近年来，电共振现象被越来越多学者研究，因为其产生的作用效果对光散射或者GH位移的影响非常显著，其中讨论最多的是电偶极共振[17]。笔者以各向异性的球颗粒为研究对象，通过理论分析和数值模拟研究了在不同参数下的GH位移，分析了各向异性参数对GH位移的影响。

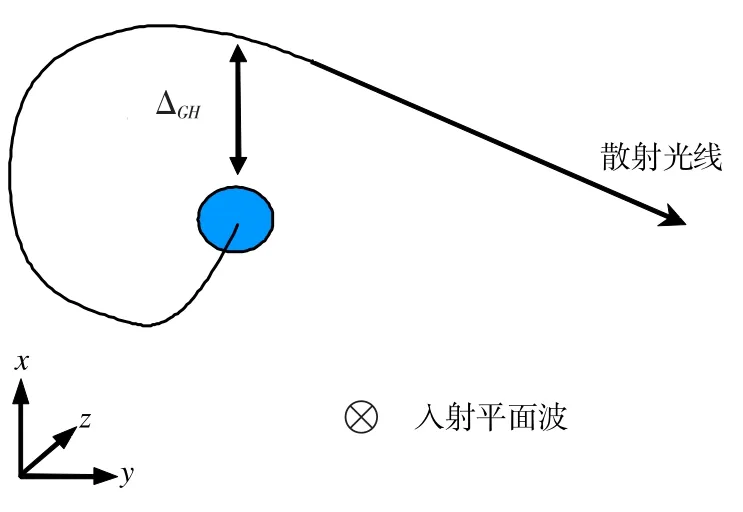
图1 研究模型示意图

1 理论计算

考虑一个半径为a的各向异性球放在介电常数ε0和磁导率μ0都为1的真空中，其相对介电常数和磁导率张量可以写成球坐标形式：，其中 εθ=εφ=εt，μθ=μφ=μt。如图1所示，一束线极化的平面波波矢为k0=，沿着z轴正方向照射过来，为简单起见，假设入射波的电场振幅为1，方向沿着x轴正方向：其中k0=2π/λ。

可以推广Lorenz-Mie散射理论，运用德拜势来严格求解各向异性球颗粒的电磁波散射。从麦克斯韦方程组出发，把球的散射波看成是横磁波（TM，特征是径向磁场值Hr=0，来自电振动的贡献）和横电波（TE，特征是径向电场值Er=0，来自磁振动的贡献）的叠加，因而矢量麦克斯韦方程组可以转化为关于德拜势的标量方程组

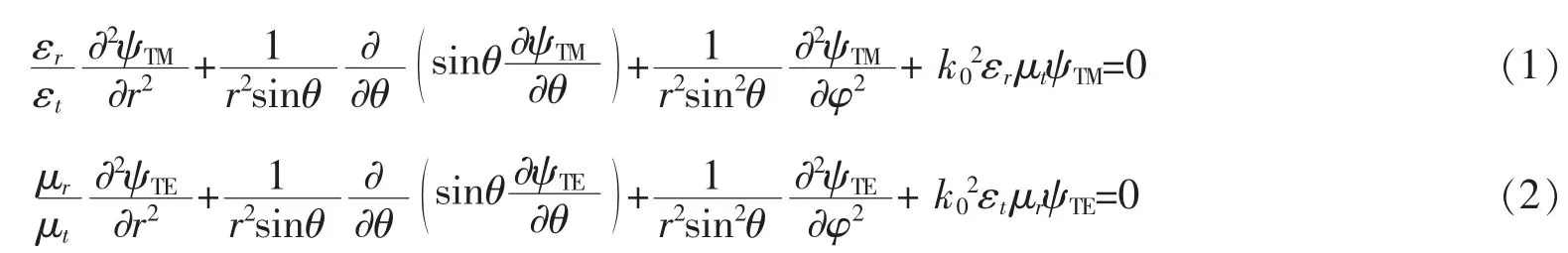
通过一些数学处理过程，可以得到各向异性球颗粒的第n阶TM和TE模式的散射系数an和bn

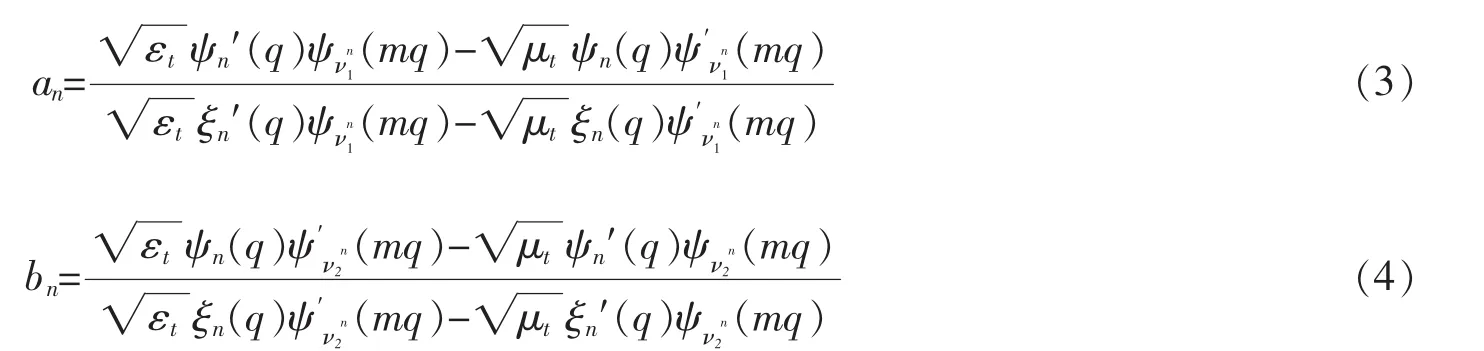
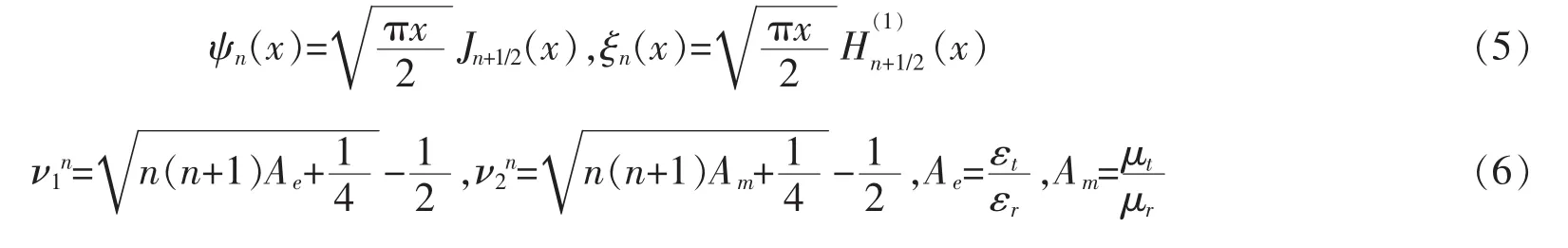
这里 Jn+1/2（x）和分别代表第（n+1/2）阶贝塞尔函数和第（n+1/2）阶第一类汉克尔函数。Ae和 Am则表示各向异性电参数和各向异性磁参数，若为各向同性，那么Ae=Am=1，表达式（3）和（4）化简之后与经典Mie理论完全吻合。

最后，GH位移可以通过以下表达式计算[18]

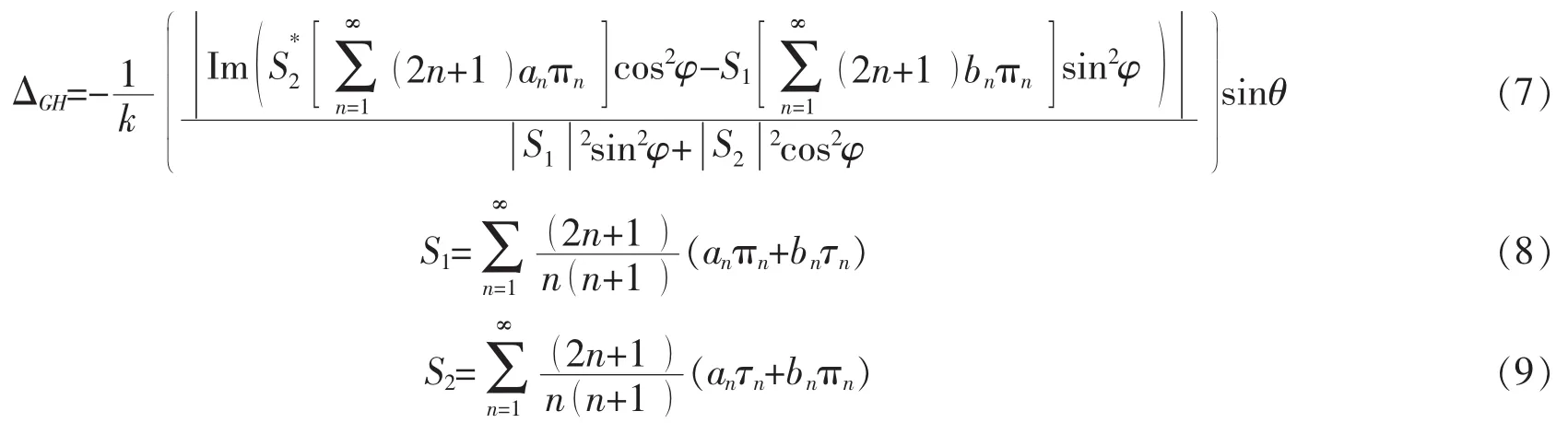
其中 πn，τn是关于 θ的表达式，其中Pn1代表勒让德函数（Legendre function）。

2 数值模拟

因为电共振对材料的光学特性一般都有所加强，近零材料由于其特殊的介电常数/磁导率可能会使得GH位移与某些参数无关，所以笔者选取电共振和近零材料两种情况研究了各向异性参数对GH位移的影响，入射波的波长都取632.8 nm。当εt=-ν11-1时，散射系数第一项的分母为0，即产生电偶极共振，不同半径的各向异性球发生电共振时GH位移与θ的关系如图2所示。当半径较小时，电共振对GH位移影响很大，主要是由于此时颗粒内部和表面会出现场增强，并且远场反射也会发生改变，通过调节电各向异性参数，可以改变GH位移的大小，由图2（a）可知：随着Ae不断变大，峰值会越来越小，并且峰值位置会渐渐向右移动。但是当各向异性颗粒半径达到340 nm或者更大时，笔者发现电共振对GH位移的影响微乎其微，并且此时各向异性参数对GH影响也不是非常显著，如图2（b）所示。

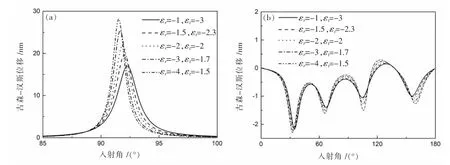
图2 μr=μt=1，半径a分别为50 nm（a）和340 nm（b）时古斯-汉森位移与入射角度的关系

随后，笔者研究了近零材料中各向异性参数对GH位移的影响。图3分别表示εr近0和εt近0时半径为50 nm的各向异性颗粒的GH位移与θ的关系。由图3可知，近零材料中的GH位移比非近零材料大得多。图3（a）表示的是εr=0.001时，改变εt对GH位移的影响。可以明显看出当εr近0时，随着εt变大，即Ae变大，GH位移的峰值会越来越小，并且峰值位置也相应向左偏移。但当εt=0.001时，εr对GH位移的没有影响，如图 3（b）所示，无论如何改变 εr，GH 位移图像均不变，主要是因为当 εt近 0时，Ae=0，散射系数与 εr的取值无关。