介观Aharonov-Bohm环的交流电导

（苏州科技大学 数理学院，江苏 苏州 215009）

对于正常的金属环，当电子的平均散射自由程大于系统的尺寸时，量子干涉效应会存在于其中。当金属环置于外磁场中，通过环中心的磁通会导致Aharonov-Bohm类型的振荡，其基本周期为Φ0=ħc/e。对于一个孤立的介观环，当它受到外磁场驱动时，其表现类似于带有Josephson结的超导环[1]，而对于开放的介观环系统，其电阻随着磁通周期性地变化[2]。Büttiker，Imry和Azbel的工作给出了这两种现象之间的一个联系[3]。同时注意到一个关于介观系统的波导理论被提出，考虑了波函数以及波函数的导数在节点处的连续性条件[4]。基于这个理论，J.Yi等人研究了对称性单环和双环结构的透射几率和持续电流[5]。

尽管关于AB环直流电导的理论研究已经十分详细，笔者认为有必要进一步探讨类似系统在交流响应下的性质。实验方面，90年代中期，Pieper和Price在介观尺度的银环中观察到了交流电导的实部和虚部在宽频尺度范围下的振荡[6]。Chen等人测量了二维电子气系统的电容系数在磁场翻转下的对称性[7]。理论方面，Büttiker已经建立了在低频范围下的线性交流输运理论[8-9]，他指出为了满足流守恒和规范不变性，载流子之间的相互作用必须考虑。电子之间的长程库仑相互作用导致系统内部存在一个随时间变化的内势，在AB环系统中，这个内势是入射粒子能量、外加磁通以及其他参数的响应函数，该内势随着端口处电化学势的变化导致了电化学交流发射率，而它随着外加磁通的变化又产生了磁通交流发射率[10]。这两种不同类型的交流发射率都可以用对应的特征函数来表示。这里的特征函数描述的是内部的静电势相对于外部参数变化的响应。而最近又有一些基于非平衡格林函数，满足流守恒和规范不变性的交流输运理论被提出[11-13]。

笔者注意到，已经有一些理论方面的计算工作，应用Büttiker的交流输运理论去处理不同介观结构中的交流响应问题[14-15]。这些工作基本上都只考虑了电化学交流发射率和它对应的特征函数。笔者主要研究的是单环和双环系统中的交流输运问题。首先，推导了这两种系统的散射矩阵，然后计算了一些重要的物理量，例如透射几率、特征函数和交流发射率。与前面所提到的那些工作[14-15]不同的是，笔者不仅考虑了电化学交流发射率，还仔细研究了磁通交流发射率。对于介观环的交流输运性质，Büttiker已经给出了一些预测。笔者的计算结果和Büttiker的预测完全一致，并且得到了许多有意义的新的物理现象。

1 物理模型及推导

Büttiker及其合作者建立了关于介观系统的交流输运理论。通常情况下对于一个介观导体，当它处在随着时间变化的外扰动（比如样品端口处所加的振荡电压和环中心所加的振荡磁通）下，会偏离它的平衡态。一个介观结构有若干端口，分别标记为k，l，… 。在端口l处加一个振荡电压δVl时，在端口k处会有一个振荡电流 δIk（ω）

电流守恒要求电导矩阵的行和列相加均为零

Büttiker对于介观系统的交流输运有着深入的理解。他指出如果不考虑电子间的相互作用，系统各个端口上的电流响应不会存在关联，同时电流守恒不会被满足。要建立一个满足电流守恒的交流输运理论，电子之间的长程库仑相互作用必须考虑。这样，在系统内部会产生一个随时间变化的静电势，电荷在样品内部累积并带来位移电场和位移电流。

一般情况下，为了得到交流条件下的电流响应，需要有三个步骤：第一步，不考虑电子之间的相互作用，只是根据散射理论给出随外部电化学势变化的电流响应；第二步，考虑由电子间的库仑关联所导致的新的注入系统的粒子数；第三步，计算出由这部分粒子所产生的内势而带来的电流响应。由此可知，交流电导有两部分贡献：一部分是相对于外部微扰的外部响应；另一部分是相对于内势的内部响应。

如果改变端口k处的电化学势，在端口l处由于外部响应所导致的交流电导是

其中dnkl（r）/dE被称为是局域部分态密度。它描述的是在位置r处，从端口l进入系统并从端口k离开系统的载流子的态密度。

交流电导的内部响应是由导体内部的静电势所生成的。此处研究的是受Aharonov-Bohm磁通驱动的介观环系统。因此，静电势是样品端口处的电化学势以及所加AB磁通的函数。笔者引入了特征函数u（r），该函数描述了导体内部的静电势随着外加电化学势的变化。这个电化学特征函数u（r）可以对比于磁通导致的特征函数v（r），后者描述的是内势相对于磁通的变化。在低频极限下，静电势的扰动可以展开成电化学势和AB磁通的微扰，对于线性项得到[16]

电化学特征函数u（r）和磁通导致的特征函数v（r）都可以利用解泊松方程得到

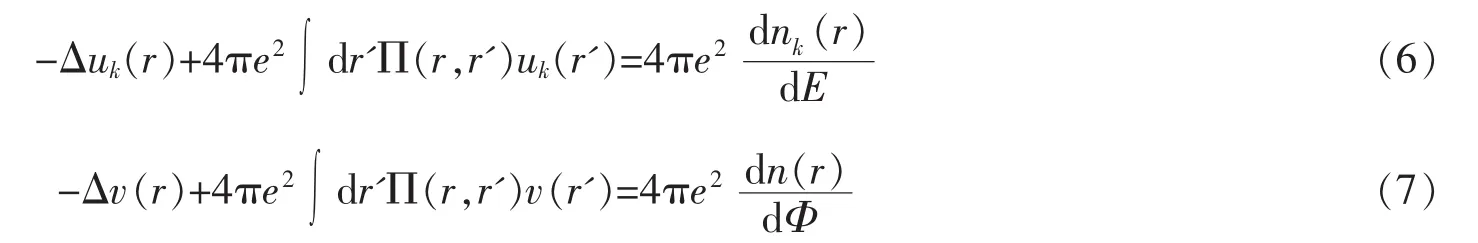
如果只考虑加在端口处的振荡电压的作用，不考虑磁通。内势U也只随dμk展开，内部响应所造成的交流电导可以表示为

这样综合公式（4）和（8），得到了在线性条件下体系总的交流电导

在公式（9）中，Gkl（0）是系统的直流电导，乘以频率ω的那一项称为交流发射率。交流发射率实际上表示了外加微扰下系统的交流响应特征，是交流输运理论中最重要的量。结合公式（4）、（8）和（9），得到了关于交流发射率的表达式

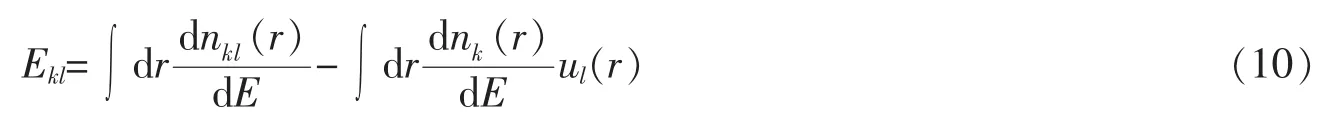
以上定义的交流发射率表示了系统内部的电荷随着外部电化学势扰动而产生的变化，称为电化学交流发射率。下面讨论磁通导致的交流发射率，它定义为导体k中积累的电荷相对于磁通Φ增量的比值。磁通交流发射率可以表示为

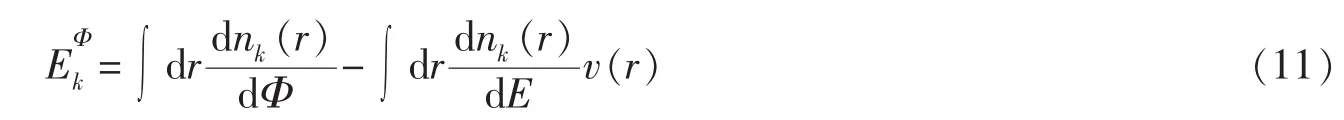
因为振荡的磁通不会产生直流的电导，所以对于上面所讨论的交流发射率，它的各个元素相加必须为零[16]

以上定义的两种类型的交流发射率都是由局域部分态密度和特征函数来表示的。为了简化计算，下面的讨论采用中性近似条件下的特征函数。这意味着特征函数u（r）和v（r）都是用部分态密度来表示

同时对局域部分态密度进行空间的积分，这样电化学交流发射率和磁通交流发射率可以简化为

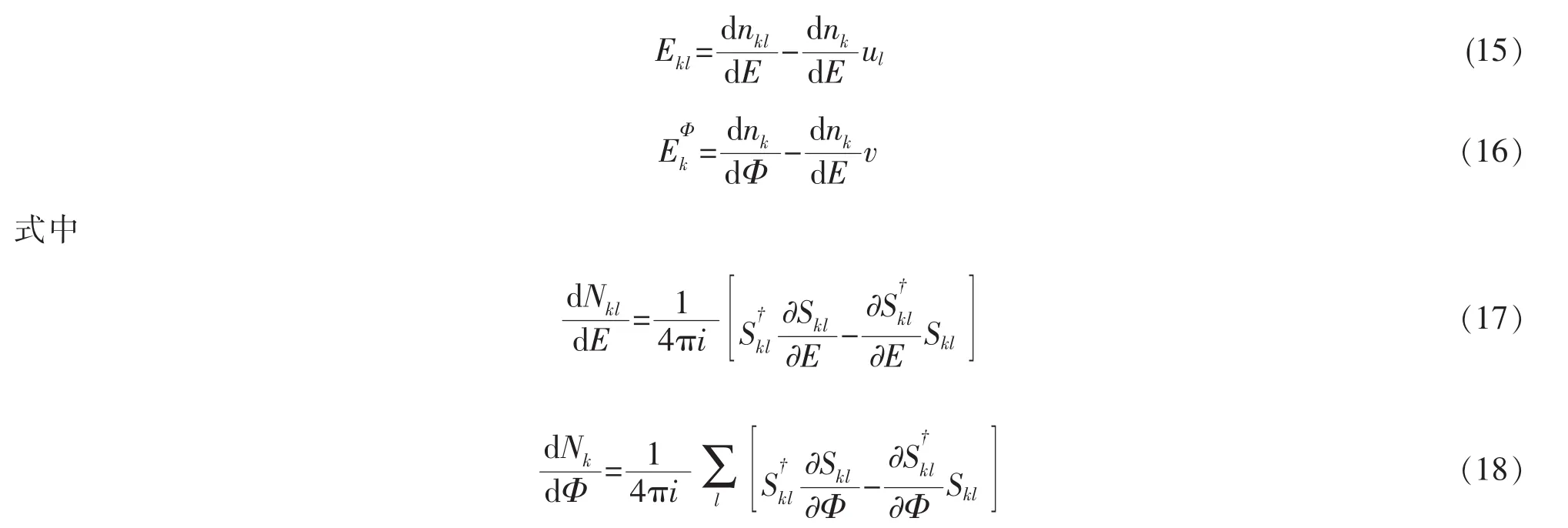
式（17）、（18）是部分态密度描述的是从端口l进入导体并从端口k离开导体的电子数。部分态密度是由系统的散射矩阵来表示的，散射矩阵元Skl定义为端口k中出射波函数的振幅相对于端口l中入射波函数振幅的比值。

笔者研究的是正常的金属环系统，图1中的（a）和（b）分别代表一维的单环和双环结构。每个环都受到外加的AB磁通Φ的驱动。整个结构通过导线连接到外部的电子库，电子从库中发射出来进入系统并最后返回到库中。在库里面，电子之间的散射是非弹性的，所以库吸收的电子和发射的电子之间没有相位方面的联系。而在环结构里面，电子只受到弹性的散射。可以将整个环和导线看作是理想的一维导线，电子的波函数可以用自由平面波来描述。

下面先推导单环结构的散射矩阵。

假设电子在导线和环的节点处受到弹性散射。这个节点可以用一个三维的散射矩阵S0来描写，该矩阵给出了三端出射波函数的振幅（α'，β'，γ'）和入射波函数的振幅（α，β，γ）之间的联系。 流守恒要求 S0是幺正的，同时时间反演不变性要求， 因此，S0也是对称的。笔者采用在参考文献[3]中给出的模型

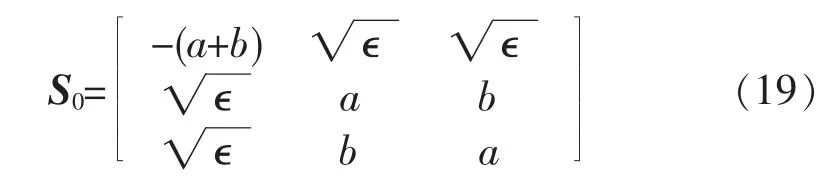
流守恒要求

这样系数a和b都可以表示为є的函数

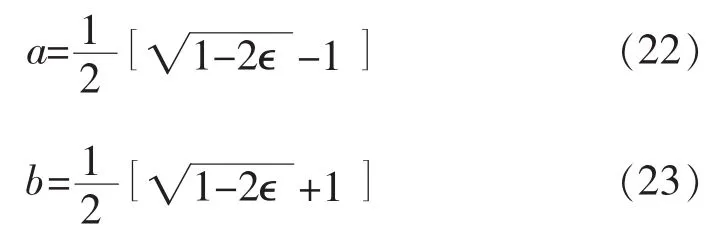
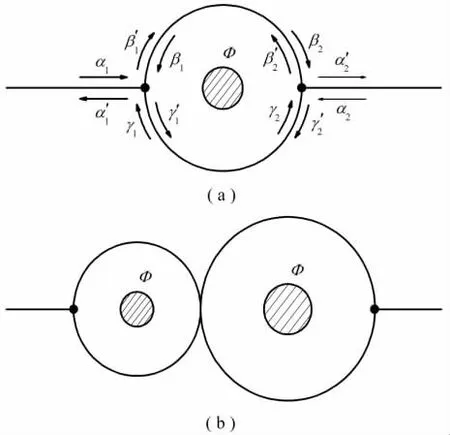
图1 一维单环（a）和双环（b）结构示意图

参数є表示环和导线之间的耦合强度，其变化范围是从0到1/2。当є处于强耦合极限1/2时，节点对于入射的粒子完全透射。另一方面，当є等于0时，入射的电子在节点处完全反射，这样环和导线实际上是没有耦合，环可以看成是孤立的系统。

先看图1（a）中单环左边的节点，散射矩阵S0给出了下面的方程组

由于环是受到磁通Φ驱动的，磁场会导致环上臂和下臂中波函数的相位分别改变φ和-φ，其中φ=πΦ/Φ0。同时由于布洛赫定理，电子波函数在环中的传播会产生另外的相位变化θ=k0L，式中k0代表的是波矢，L表示环的半周长。这样可以得到环上臂左右节点处的电子波函数之间的联系

同样类似得，对于环的下臂有

对于环右边的节点，同样用前面所定义的散射矩阵S0来描述

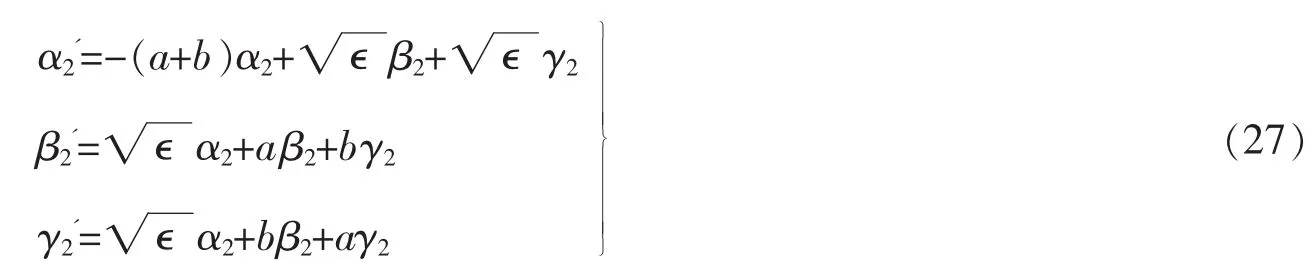
通过解方程组（24）-（27），推导出了整个单环结构的散射矩阵

矩阵中的r是反射振幅，而t是透射振幅，它们的形式是

最后还可以由透射振幅t得到单环结构的透射几率Ts

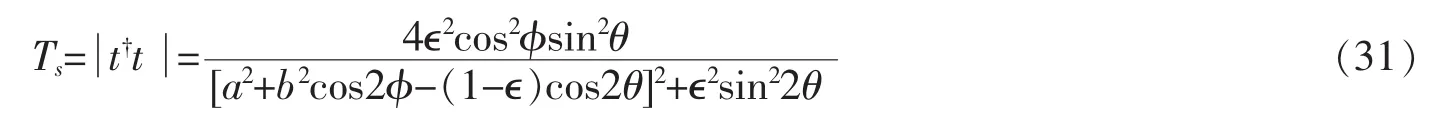
前面推导了单环结构的散射矩阵。对一个散射系统来说，当得知了它的散射矩阵时，可以很自然地求出它的转移矩阵。下面给出二维系统中散射矩阵和转移矩阵的表达形式

通过比较散射矩阵和转移矩阵各个矩阵元之间的关系，可以求得单环结构的转移矩阵

下面采用传输矩阵的方法来求解双环结构的散射矩阵。先从普遍情况出发，考虑非对称的双环结构，如图1（b）所示。左边的环和右边的环大小不等，但所加的磁通相同。定义左边环的散射矩阵为S1，转移矩阵是T1。右边环的散射矩阵和转移矩阵分别为S2和T2。这样整个双环结构的转移矩阵可以通过相乘T1和T2求得

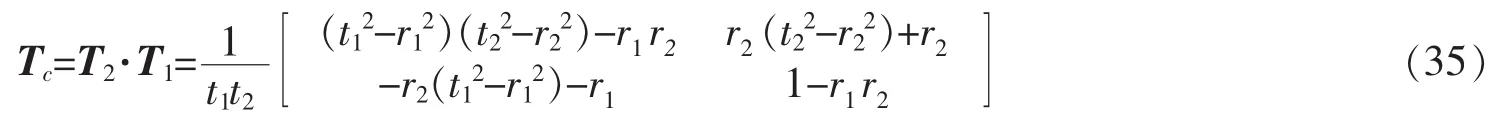
根据方程（32）和（33），可以反过来求得双环结构的散射矩阵

每个矩阵元都可以用单环的反射和透射振幅来表示

现在研究对称的双环结构，左边和右边的环大小完全相等，所加磁通也一样，这样两个环的转移矩阵完全相同。

参照前面已经推出的单环的反射和透射振幅，方程（39）现在可以写为

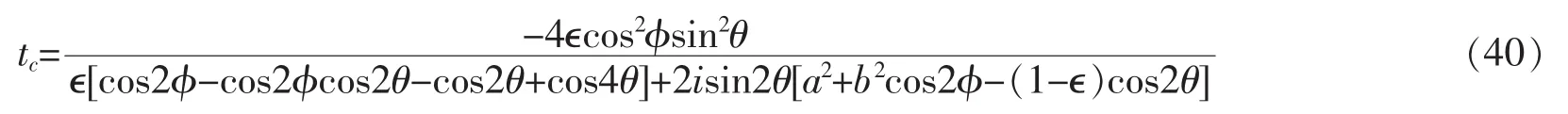
还推导出双环的透射几率

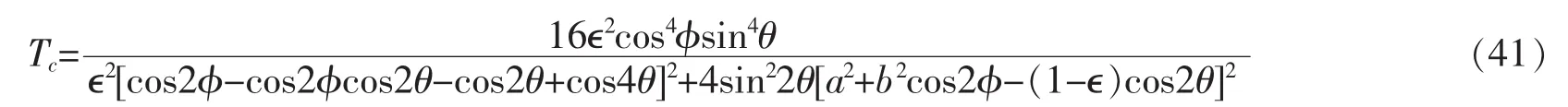
由以上表达式可以计算单环和双环系统中的直流电导和交流响应，在计算交流发射率时，用到的最重要的量是部分态密度。就像在处理平衡态物理系统时需要用到态密度一样，在处理非平衡态问题时，部分态密度会非常有用。实际上部分态密度矩阵的非对角元对于描述交流输运中电子的涨落和关联起决定作用。在下一部分，给出单环和双环系统的透射几率、特征函数以及交流发射率的数值计算结果。

2 结果和讨论

众所周知，一个介观体系的直流电导可以通过Landauer-Büttiker公式和体系的透射几率直接联系起来g（0）=2e2T/h。 图2给出了单环结构和对称双环结构的透射几率T随着入射粒子能量的变化图。

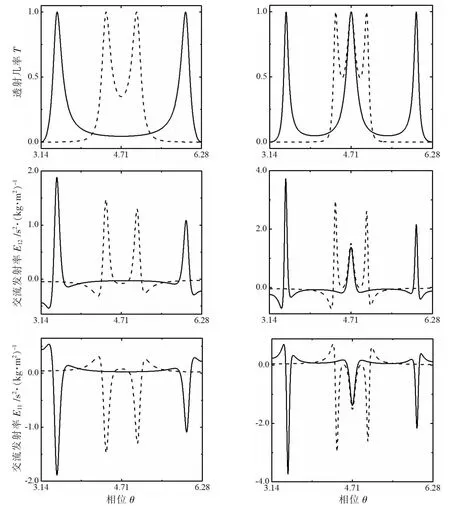
图2 单环（实线）和双环（虚线）结构的T，E12和E11相对θ的变化

入射粒子的能量可以用 θ来简化表示，θ=k0L=（2mE/ħ2）1/2L。环和导线之间的耦合强度є固定在1/6，每个环的半周长都取为100 nm。从图2中可以看出单环和双环的透射几率都是θ的周期函数，环中心所加的磁通决定了共振峰的位置。这里的物理图象可以理解为，环和导线的节点可以看成一个势垒，所以单环结构类比于双势垒系统，磁通改变了两个势垒之间的距离从而直接改变了共振峰的位置。

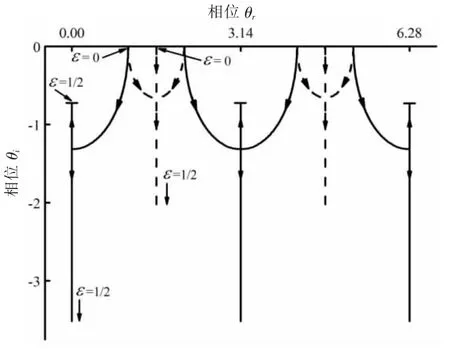
图3 单环和双环的T的极点随着є的变化

Büttiker已经在参考文献[3]中指出，单环结构中透射几率的共振峰可以表达成Breit-Wigner公式的形式，他证明了当耦合参数є变大时，透射几率共振峰的峰宽会增加，而幅度会减弱。可以从图3中更好地理解这种性质。图3给出了透射系数的极点在复能量空间中随着耦合参数є变化的曲线。图中实线代表的是单环，虚线代表的是双环，加在环中心的磁通取φ=π/3。相位θ的实部θr代表共振峰的位置，虚部θi则意味着共振峰的峰宽。在є=0时，极点是在实轴上面，所在的位置对应于系统的本征能级。笔者注意到双环结构的三个本征能级有两个和单环一样，另一个则在θr=（2n+1）π/2处，其中n为整数。此处讨论的本征能级对应于图3中共振峰的位置，另外发现双环结构的共振峰要比单环结构来得窄。Büttiker指出共振峰的峰宽正比于耦合参数є，在图3中当极点偏离实轴时，单环є的增加的比双环要快。

现在讨论电化学交流发射率的性质。从前面推导的公式可以得知，交流发射率实际上代表了交流电导的虚部。交流发射率矩阵的每个元素都是由电容效应或电感效应所主导。为了有助于理解它的含义，可以对比参照经典电路中的组件，比如电容C和电感L。与这些经典电路元件一样，交流发射率出现在介观系统交流电导g=g0+iωX的虚部，X代表电荷之间的相互作用而产生的动态阻抗。在图2中，给出了电化学交流发射率E11和E12相对于入射粒子能量的变化函数，并且给出了这两种交流发射率和系统透射几率的对比。从数值计算结果不难看出，电化学交流发射率在系统的共振能量附近有着非常剧烈的变化。计算结果表明，当入射粒子的能量非常接近系统的共振能量时，对角元交流发射率E11为负值。这是一种类似于电容的效应。而非对角元交流发射率E12为正值，这代表的是电感的效应。E11和E12曲线的形状完全相反，这是流守恒和规范不变性所要求的ΣkEkl=ΣlEkl=0。对应于透射几率的每个共振峰，交流发射率表现出一种有趣的性质。以图2中的E12为例，在系统的共振能量处，交流发射率都显示出了一个正的尖峰。但当入射粒子的能量逐渐偏离共振能量时，交流发射率的数值会迅速减小，并且由正值转变为负值。在每个共振能级的两边，E12都会达到一个负的极大值，然后渐进趋向于零。

下面讨论交流发射率电容和电感特性产生的物理机制。当入射粒子的能量等于系统的共振能量时，透射几率会最大。在直流的情况下，电子会直接穿过系统，但在交流的环境下，电子会在系统内部驻留，波函数的相位也会被延迟。实际上，非对角元交流发射率E12和E21反映了两种因素的竞争。从方程（10）和（15）可以看出交流发射率由两项组成：第一项部分态密度是正的，它反映的是电子在系统的两个端口之间直接输运所带来的电感效应；第二项明显是负的，它反映的电荷在系统内部累积所产生的电容效应。正是这两种因素之间的相互竞争导致了交流发射率在共振能量附近出现了特殊的变化。

从图2中还可以看出交流发射率每个共振峰的振幅会随着入射粒子能量的增加而减弱。这个性质是可以理解的，由于交流发射率反映了系统的交流振荡效应，当整个体系的能量增加时，外部的扰动则会相应地减弱。同时注意到，双环结构交流发射率的振幅几乎就是单环结构的两倍，这说明了当环的数目增加时，系统的交流响应会成倍地放大。

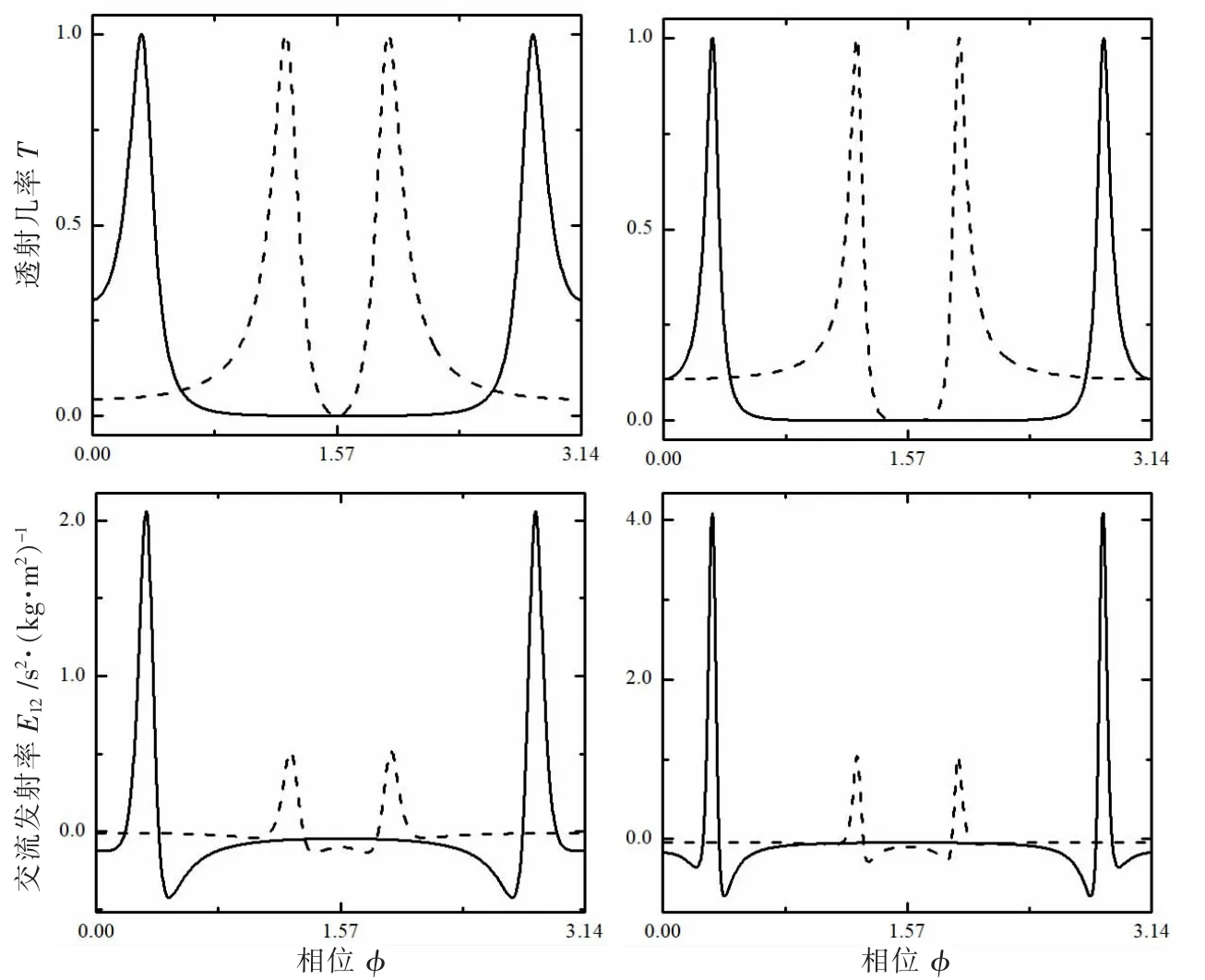
图4 T和E12作为磁通φ变化的函数

图4给出了电化学交流发射率E12和透射几率T随磁通变化的曲线。考虑了不同入射粒子能量的情况，θ=0.1π和θ=0.4π。很明显交流发射率和透射几率T一样，都是随φ变化的周期函数，基本周期为Φ0=ħc/e。这个性质Büttiker已经给出了预言，因为电子之间的长程库仑相互作用会使系统的态密度随磁通 φ周期变化。图4表明了交流发射率的大小主要由入射粒子的能量而不是外加磁通决定，因为对应于θ=0.1π的曲线的振幅远远大于对应于θ=0.4π的曲线的振幅。

最后讨论磁通导致的交流发射率。磁通交流发射率主要是由样品内部的态密度对于磁通的敏感响应引起的。Büttiker指出，这种响应只会存在于不具有空间旋转不变性的结构中[10]。在此，完全对称的单环和双环结构中不存在磁通交流发射率，它只存在于非对称的双环结构中。首先考虑一种特殊的情况，入射粒子的能量保持不变，两个环大小的不等导致了相位因子θ的不同，设θ1=0.4π并且θ2=0.41π，下标1和2代表左边和右边的环。在图5中先画出了对应于磁通的特征函数v在不同的耦合强度є下随φ变化的曲线。很明显v是φ的周期函数，这意味着系统内的静电势同样是磁通的周期函数。可以看到随着耦合参数є的变大，v的最大值减弱。这种性质也类似地出现在连接到单一库的单环的持续电流中[17]。 Büttiker也曾经指出磁通导致的电容和持续电流之间会存在某种联系[10]。

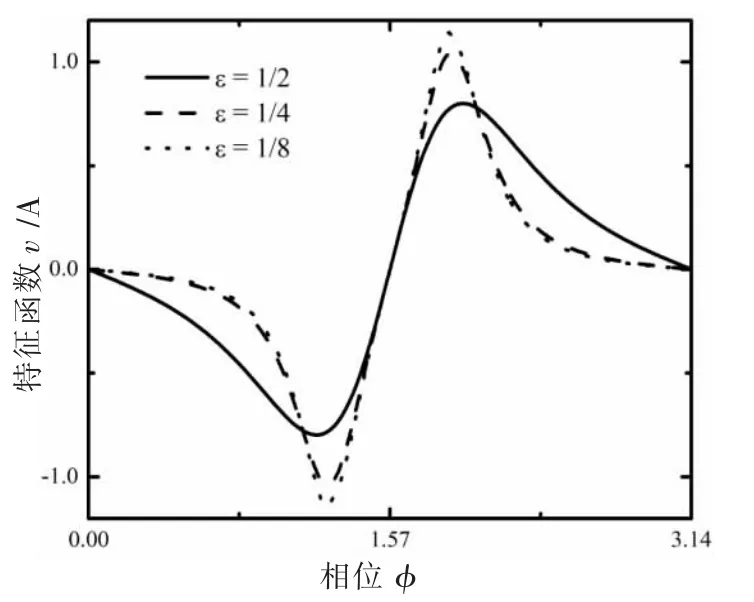
图5 特征函数v在不同的є下随φ的变化

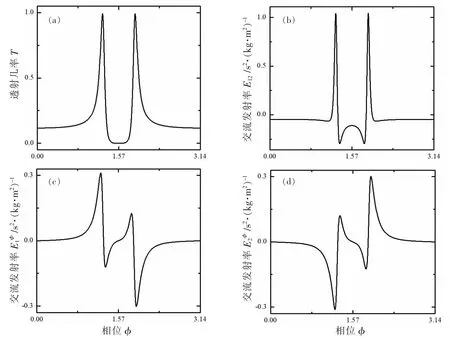
图6 T（a）、E12（b）、E1Φ（c） 和 E2Φ（d）相对于 φ 的变化

图6给出了非对称双环结构的透射几率T、电化学交流发射率E12、磁通交流发射率E1Φ和E2Φ相对于φ变化的函数。由图6可见，磁通交流发射率E1Φ和E2Φ同样在共振能量附近作剧烈的变化。与电化学交流发射率E12所不同的是，E1Φ和E2Φ都是磁通φ的周期奇函数，而前者是磁通φ的周期偶函数。这个性质的物理本质是在计算这两种不同的交流发射率时所用到的Lindhard函数相对于磁通翻转时所具有的不同对称性。E1Φ和E2Φ曲线的形状完全相反，这个性质在前面的推导中已经讨论过。

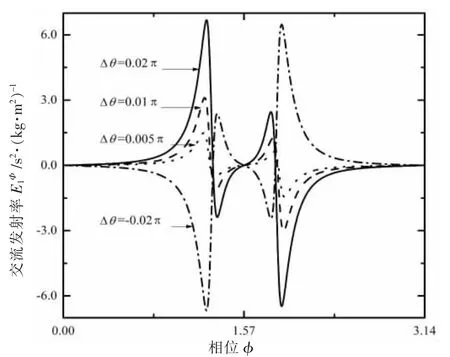
图7 E1Φ在两个环大小差异不同时的分布

最后考虑两个环大小差异的程度对交流发射率E1Φ和E2Φ的影响。图7给出了清晰的说明，在此用Δθ标志两个环的差异。由图7可见，当两个环大小的差别不是很大时，交流发射率E1Φ曲线的形状基本上一样。只是共振峰的最大值随着Δθ的增大而线性地增大。当Δθ取负值，也就是两个一大一小的环左右调换位置时，E1Φ的取值完全翻转过来，和原来的E2Φ一样。这些都是关于磁通导致的交流发射率的特殊性质。

3 结语

利用Büttiker的交流输运理论，仔细研究了介观尺度下一维单环和双环结构中的交流电导。通过数值计算，得到了系统的透射几率、电化学交流发射率和磁通交流发射率等一些物理量的计算结果和物理性质。发现交流发射率在系统的共振能量附近发生剧烈的变化，并且呈现出电感和电容的物理效应。透射几率和交流发射率矩阵的系数都是所加磁通的周期函数，并且交流发射率的大小主要由入射粒子能量决定，而不是受磁通影响。发现了电化学交流发射率和磁通交流发射率相对于磁通呈现出不同的对称性，数值计算结果表明，磁通交流发射率是随磁场变化的奇函数，而电化学交流发射率是随磁场变化的偶函数。关于这个性质Büttiker曾经在以前的工作中做出了预测，笔者的计算结果很好地验证了他的观点。