基于Spark的肿瘤基因混合特征选择方法

汪丽丽,邓 丽,余 玥,费敏锐

(1.上海大学 机电工程与自动化学院,上海 200072; 2.上海市电站自动化技术重点实验室,上海 200072)

0 概述

基因芯片技术可快速检测成千上万基因的表达水平,对了解基因功能、开展生物学研究等具有重要意义。文献[1]通过检测一组特异基因的表达水平进行肿瘤亚型的诊断。随后大量研究人员展开将基因数据用于肿瘤诊断及亚型分类的研究。肿瘤基因数据往往样本数量少而基因数量非常庞大。数据中的大量无关基因及冗余基因会对分类产生一定影响。有研究表明[2],在肿瘤基因数据处理过程中,选择特征基因子集往往比选择高效分类器更为重要。

传统特征选择分为过滤式(filter)与封装式(wrapper)。过滤式依据某一标准给特征赋予一定的权重,具有收敛快、计算复杂度低等优势,如F-score[3]、互信息等。封装式将后续学习器的性能作为特征子集的评价准则,学习器包括扩展的线性模型(回归模型[4]、线性支持向量机[5-8])、基于树的方法(随机森林[9-11])等。混合特征选择结合过滤式和封装式,比过滤式分类效果更优,比封装式计算更快[12-13]。近年来,集成特征选择算法受到研究学者们的广泛关注。集成特征选择方法通过数据扰动或功能扰动方法,独立构造不同学习器进行特征选择,集成各个结果获得最终特征子集[14]。一些学者结合混合特征选择和集成特征选择实现更优化的特征选择,如:基于FCBF及ABACO、IBGSA 2种启发式算法的集成方法[15];基于Relief、IG、FCBF集成方法及ABACO算法[16];基于信噪比和条件信息相关系数(CCC)集成方法[17]。

F-score[3]算法简单、运行速度快,有助于理解数据但主要对线性关系敏感。SVM递归特征消除(SVM-RFE)[5]算法稳定能够反映出数据的内在结果。针对多标签问题可拓展为多分类SVM-RFE(MSVM-RFE)[6-8],但往往不能全面地考虑特征与每个类别的关系。基于随机森林的特征选择准确性高,适合多分类问题,但对于关联特征的打分不稳定[9-11]。随机森林特征选择和MSVM-RFE对于挖掘非线性关系有较好的效果。集成特征算法如要得到较好的集成效果,集成学习器之间必须呈现差异性[18],所以采用功能扰动方法集成这3种差异性较大的特征选择方法可实现优缺点相互补充,提取出包含最多类别信息的特征子集,以便开展后续的生物学研究。

目前,基因数据的处理分析大多都是在单台机器上实现的。然而随着基因数据规模逐步扩大,单机处理运算能力不足的缺陷逐步显现。分布式计算框架的出现使存储及处理海量数据成为可能。Spark立足于弹性数据集,数据缓存在节点内存,适合基因数据处理过程中存在的大量迭代运算。

综上所述,本文提出一种基于Spark分布式计算框架的混合特征选择方法。该方法利用F-score去除无关基因,通过集成F-score、MSVM-RFE、基于随机森林的特征选择3种方法得到特征子集,最终实现SVM分类预测。

1 肿瘤基因数据的混合特征选择

1.1 Spark分布式框架

Hadoop框架一直是首选的大数据处理方案,但从Map任务到Reduce任务,数据被写入磁盘从而产生大量信息通信,并不适合处理迭代任务。Spark分布式框架基于弹性分布式数据集(RDD),数据被缓存在工作节点的内存中,适合进行机器学习及智能优化算法中的迭代运算。数据集操作不仅包括Map和Reduce操作,还提供很多函数转换(transform)、数据执行(action)等操作。

本文将Spark运行在现有的Hadoop集群基础上,通过读取HDFS上文件创建弹性分布式数据集RDD,在RDD分区的工作节点上分别执行肿瘤基因数据的特征选择操作,执行后结果被发送到驱动程序进行聚合,最后将结果返回到HDFS平台上。

1.2 分布式混合特征选择实现

分布式混合特征选择的主要思路是首先用过滤式特征选择,在不影响分类正确率的基础上,去除无关基因,然后分别进行3种不同的特征选择,集成不同的选择结果作为最终的特征子集,最后用支持向量机进行分类检验,混合特征实现框图如图1所示。

图1 混合特征选择实现框图

分布式混合特征选择实现步骤如下:

步骤1从HDFS上读取肿瘤数据集,创建一个弹性分布式数据集。

步骤2通过Map操作将文件每行的数据用“,”隔开,通过LabeledPoint来存储标签列和特征列。

步骤3采用F-score特征选择方法去除无关基因,并用支持向量机进行分类检验。

步骤4对上一步得到的初选特征子集分别采用F-score、MSVM-REF、基于随机森林的特征选择3种方法,每种方法输出选择的特征子集,选择出现最多次数的特征为最终特征选择子集。

步骤5利用最终的特征选择子集运行在支持向量机上,采用十折交叉验证计算子集的分类正确率。

1.3 F-score及支持向量机分类检验

肿瘤数据成千上万的基因中有90%以上的基因都是与分类无关的,所以可以通过F-score粗略地计算每个基因与类别之间的关系,在不降低分类准确率的条件下,去除这些无关基因。通常有2种方法来确定初选特征子集的基因数方法:按照经验选择或根据某些准则自动确定。本文首先依据相关的文献资料,确定基因数为100～200之间,然后逐渐减少基因数进行若干次实验并记录分类结果,直到基因数下降而特征子集的分类正确率基本保持不变则停止。确定选择基因数的初选过程如下:

1)F-score特征初选

初始数据集RDD1={(x1,y1),(x2,y2),…,(xN,yN)},其中,xi=〈xi1,xi2,…,xin〉为n维向量,n为总基因数,yi取0,1,…,m中某一值,m为标签类别数,N为样本数。通过F-score计算每个特征与标签类别之间的关系,计算公式为:

(1)

2)对上述阶段得到的初选特征子集进行SVM分类检验

本文采用的支持向量机是在基本型的基础上引入“软间隔”概念,并采用hinge损失,SVM目标函数为:

(2)

传统的SVM求解是引入拉格朗日乘子得到对偶问题,通过SMO算法求解对偶问题。在分布式计算框架下,不需要转换成对偶问题,而是直接针对目标函数利用随机梯度下降(SGD)优化技术求解,在每次迭代中计算梯度和、损失和以及更新权重,直至收敛或达到指定次数。其中,随机梯度下降更新公式为:

(3)

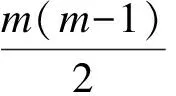
1.4 集成特征选择

对初选特征子集RDD2分别进行F-score、MSVM-REF、基于随机森林的特征选择,每个特征选择方法都将特征子集作为输出,得到RDD3、RDD4、RDD5。结合3个特征子集计算出现次数最多的特征,将放入最终特征子集RDD6中。

1.4.1 F-score特征选择

F-score在Map阶段根据式(1)逐个计算RDD2中每个特征与标签类别之间的相关性,在Reduce阶段依据得分按降序排列,选择q个相关性最大的特征,保存为弹性数据集RDD3。

1.4.2 MSVM-REF特征选择

SVM-REF特征选择过程是基于SVM最大间隔原理的迭代选择方法。从原始特征集开始,每一次迭代通过训练模型生成权向量,得到每个特征的得分,去掉得分最低的特征,当剩余特征数达到预先设定值时,则停止迭代。由于肿瘤亚型诊断中常出现多分类问题,因此采用多分类支持向量机递归消除(MSVM-RFE)。最早的MSVM-RFE(OVA-RFE)采用OvR策略将多分类问题拆分成多个二分类任务,分别计算特征重要性,将多个得分相加后得到排序总分以此作为特征剔除的依据。OVA-RFE并不能保证最后的特征子集能同时最小化评价函数,所以采用对OVA-RFE扩展的MSVM-RFE。首先利用线性加权法将问题转换为以下形式:

(4)

利用OBD算法解决该最优化问题得到:

(5)

算法1多分类支持向量机递归消除

输入初选特征子集RDD2,设定的特征选择数q

输出被选择的特征子集RDD4

1.初始化

1.1.读入初选特征子集RDD2为集合S;

1.2.设置k为特征集S中特征数;

2.重复以下步骤,直到k=q:

2.1.用集合S训练多分类支持向量机模型,得到m个权重向量w1,w2,…,wm,其中wr=[wr1,wr2,…,wrk]T;

2.2.计算评价指标,得到特征i对应的得分ci=∑rwri2;

2.3.找出得分最小的特征z=argminici,将此特征z从集合S中除去;

2.4.设置k为集合S的特征数;

3.返回集合S为RDD4。

1.4.3 基于随机森林的特征选择

随机森林的特征重要性度量方法是通过计算平均值的方法,来收集底层树的特征重要性并将其整合。由于一棵决策树顶部的特征对大部分输入样本的最终预测决策有一定贡献,因此某一特征作用的部分样本可以用来作为对该特征相对重要性的估计。通过在多棵随机树中取这些相对重要性的平均值,可以减少这种估计的方差。特征的重要性被认为是该特征带来的某一标准的总减少量,在本文中此标准为Gini不纯度。

初选特征子集RDD2包含m个类别和N个样本,最初的Gini不纯度为:

(6)

其中,pj表示第j类样本出现的概率。若经过一次分割,样本集被分为k个部分R1,R2,…,Rk,样本数分别为m1,m2,…,mk,此时的Gini不纯度为:

(7)

分割前后Gini减少量为Gini特征重要性(Gini Important),即:

GiniImportant=Gini-Ginisplit

(8)

Gini特征重要性越大,代表该特征越重要,所以将其作为算法2中衡量特征重要性的一大指标。

根据不纯度减少原则来选择基因存在一个问题,即相关的多个特征选择一个特征后,其他特征的重要性就会急剧下降,不利于了解每个特征的重要性,容易造成误解。每次训练学习器选择的特征子集差异性较大,不利于下一步选择结果的集成,所以采用一种贪心算法-序列后向搜索算法来改善。每次迭代从特征集合中去掉重要性得分最低的特征,通过多次迭代最终得到特征数目少且分类效果优的最优特征子集。具体步骤如算法2所示。

算法2基于随机森林的序列后向特征算法

输入初选特征子集RDD2,设定的特征选择数q

输出被选择的特征子集RDD5

1.初始化

1.1.读入初选特征子集RDD2为集合S;

1.2.设置k为特征集S中特征数;

2.重复以下步骤,直到k=q:

2.1.对数据集S有放回地抽样分成n个子集,分配到各个计算节点;

2.2.创建多个map任务,利用n个训练子集构建n棵对应的决策树,计算每棵决策树分裂过程中的每一个特征变量的特征重要性GiniImportanti;

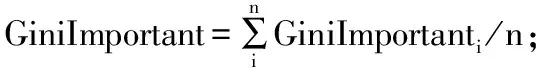
2.4.找出重要性得分最小的特征,将其从集合S中除去;

2.5.设置k为集合S的特征数;

3.返回集合S为RDD5。

1.5 支持向量机参数调整

在利用随机梯度下降求解SVM超平面参数时,有3个主要参数需要设置:迭代次数,步长以及正则化参数C。在SGD中,一开始增加迭代次数可以提高分类器性能,一旦完成特定次数迭代后,再增大迭代次数对结果的影响较小,所以希望选择一个与该特定次数相接近的值。步长是决定算法在最陡的梯度方向上前进的距离。步长越大,SGD收敛速率越快,但会导致收敛到局部最优解。正则化可通过控制模型的复杂度防止模型出现过拟合。当正则化参数选取过小,对模型性能的改变随之减少;当参数过大又会导致欠拟合降低模型性能。

为了进行这3个参数的调优,创建2个辅助函数:trainParams函数与trainMetric函数。trainParams函数给定输出参数然后训练SVM模型,trainMetric函数计算该模型对应的分类正确率。首先给定参考序列,执行Map数据转换操作,对序列元素逐一进行trainParams、trainMetric函数操作,然后再执行数据执行操作,输出不同参数及其对应分类结果,选择分类效果最优对应的参数即为最优参数。

2 实验结果与分析

2.1 运行环境的搭建与设置

本文的计算机集群包括2台计算机,其中一台计算机同时作为主节点与工作节点(Intel Core i3-6100 CPU @3.70 GHz),另外一台作为工作节点(Intel Core 2 Duo CPU E8200 @2.66 GHz)。内存分别为8 GB、4 GB。Spark分布式环境是部署在Ubuntu系统上,依次安装JDK、Hadoop、Spark以及Python,并设置SSH(Secure Shell)免密码登录,便于操作工作节点。计算机集群硬件及软件版本配置情况如表1所示。

表1 集群软硬件信息

2.2 肿瘤基因数据集及预处理

本文使用结肠癌(Colon)、乳腺癌(Breast)、儿童小型圆形蓝细胞肿瘤(SRBCT)、白血病(Leukemia)数据。数据集可从UCI、GEMS网站下载,4个数据集的基因数、样本数、标签类别如表2所示。其中,Colon、Breast数据集标签为患病样本或正常样本,SRBCT、Leukemia数据集标签为不同亚型。

表2 肿瘤数据集

2.3 结果分析

2.3.1 F-score实验分析

F-score作为初步的特征选择,要求在不降低分类正确率的前提下去除无关基因及相关性较低的基因。本文分别对3个数据集进行F-score特征选择,选择基因数为100,用支持向量机进行检验,其分类正确率与不加特征选择情况对比如表3所示。

表3 F-score特征选择前后结果比较

由于样本数量的限制,因此本文采用十折交叉验证,将10次结果平均值作为最终分类正确率。对比实验结果可知,F-score选择特征基因子集后,分类正确率不仅没有下降,反而由于去除了无关基因,分类正确率在一定程度上有所上升。实验结果表明,利用F-score选择100个特征基因能很好地保留与分类密切相关的特征基因。

2.3.2 集成特征选择算法实验分析

集成特征选择算法分析方法如下:

1)各种方法的参数选择

在求解支持向量机时,有3个参数需要设置:即迭代次数、步长和正则化参数。3个参数的参考序列分别为Seq(1,5,10,30,50,100)、Seq(0.001,0.01,0.1,1.0)、Seq(0.001,0.01,0.1,1.0,10.0)。当单独使用SVM计算特征子集的分类正确率时,通过多次训练模型,在序列中搜索最佳参数。当使用SVM用于特征选择时,SVM迭代次数、步长、正则化参数取固定值,分别为50、0.01、0.01。

在随机森林中,选择决策树个数为100,原始的序列后向算法每次迭代消除一个特征,但由于随机森林模型本身计算成本较高,训练消耗时间较大。因此,希望通过在每次迭代中消除几个特征来降低计算复杂度,但是增加迭代消除特征数可能会导致算法性能的下降。因此,在Colon、Breast、SRBCT、Leukemia数据集上分别设定特征消除数为1、2、3,训练随机森林模型进行特征选择,对不同特征子集皆采用十折交叉验证计算分类正确率,记录数据如图2所示。由图2可知,当迭代消除数为1和2时,分类准确率相差不大,当迭代消除数为3时,会下降多一些,所以选择迭代消除特征数为2。

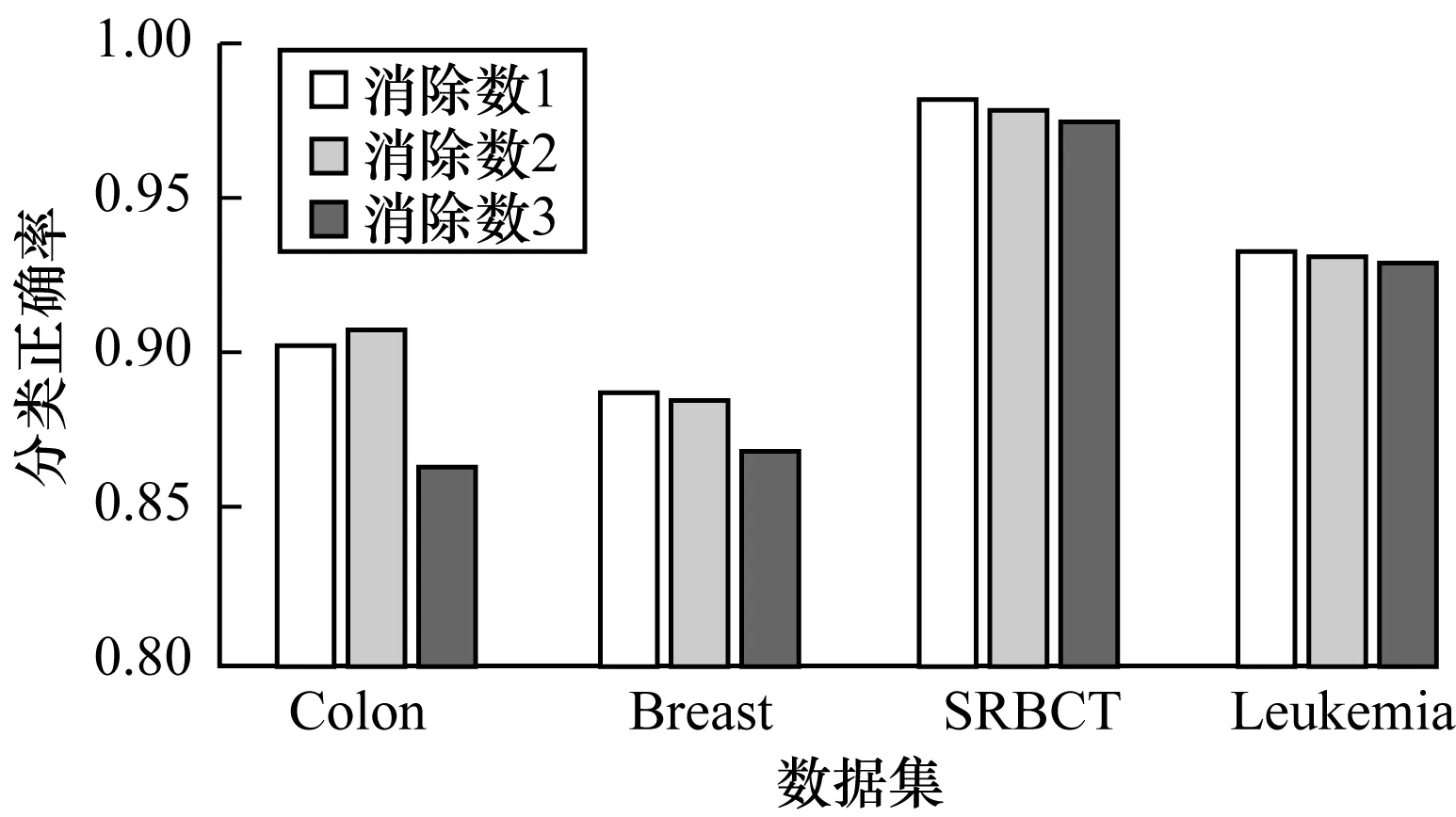
图2 随机森林参数选择

2)集成特征选择与子特征选择对比

在初选特征子集基础上,分别进行F-score、MSVM-RFE、基于随机森林的特征选择以及集成特征选择算法4种特征选择方法,记录选择不同特征数时对应的分类正确率,绘制折线图如图3所示。折线图横轴为选择的特征数,纵轴为支持向量机分类正确率。预期的特征选择效果是随着选择的特征数增加,分类正确率随之上升,达到一定值后保持不变,或者一定程度下降。实验结果与预期大致相符,在达到某一最大值之后,特征数的增加不能带来正确率的上升,正确率会在一定值上下浮动。

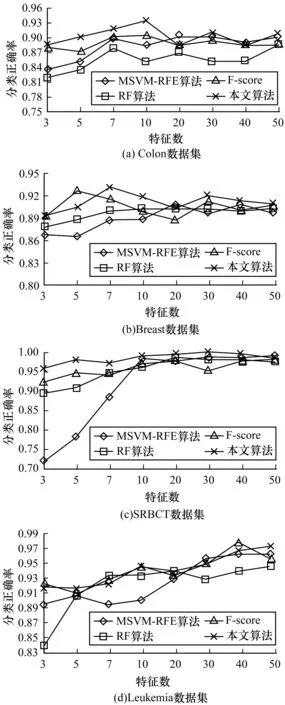
图3 特征选择对比折线图

从图3可以看出,在Colon、Breast、SRBCT数据上,集成特征选择效果相比F-score、MSVM-RFE、基于随机森林的特征选择效果有一定程度提升,尤其是在基因个数较少的时候有较好的分类正确率。在Leukemia数据上,集成特征选择算法与基于随机森林的特征选择方法效果相差不大,但仍优于F-score、MSVM-RFE运算效果。出现这样的原因主要是因为在微阵列技术中会对微阵列数据进行归一化,矩阵文件每个值为2个信号的差值,可能为负值或极小值。Colon、Breast、SRBCT数据皆为正值,而Leukemia数据存在一些负值,这些负值不仅不具有生物学意义,还在一定程度上会影响实验的结果。由于引入随机性随机森林的抗噪能力较好,因此在Leukemia数据上基于随机森林的特征选择效果较好,另外2种特征选择效果并不佳,那么集成3种特征选择方法并不能产生更好的效果,只能维持与相较最好的特征选择方法相似的效果。对于这些数据点,应该在特征选择前置为缺失或赋予统一的数值。大体上,集成特征选择方法能充分考虑特征与标签之间线性与非线性关系,特征子集的分类效果在整体上优于子特征选择方法,实验表明,集成特征选择能提取出一组数量更少、更具有结果分类能力的特征基因子集。

3 结束语

为解决肿瘤数据急剧增长导致的单机运算能力不足的问题,本文基于Spark分布式计算框架提出一种混合特征选择方法。首先利用F-score特征选择方法去除无关基因,保留与分类密切相关的基因。然后集成F-score、MSVM-REF、基于随机决策树的特征选择3种方法,得到最优的特征子集。最后采用支持向量机分类器对特征子集进行分类预测。实验结果表明,本文算法能提取特征数量少、分类效果好的特征子集。由于最优的特征选择和分类要建立在有效的数据预处理的基础上,因此下一步将从以下2个方面进行改进:融合多个相关数据集生成一个信息量更大的数据集,得到更为可靠的分析结果;增加集群节点数减少算法运行时间。