基于不同概率密度估计方法的朴素贝叶斯分类器

王乐慈，高世臣，林孟雄，李宗贤

(1.中国地质大学(北京)数理学院，北京 100083；2.中国石油长庆油田公司第五采气厂，陕西 西安 710000)

0 引 言

分类技术是一种通过学习而获得的基本技术，在模式识别、数据挖掘以及机器学习等领域作为主要研究内容。通过构建分类器进行分类识别，是一个归纳学习的过程。在实际应用中，我们需要根据训练数据的特征及规律学习并归纳出属性和类变量之间的函数关系或规则，然后对测试数据中的相关的属性配置信息，通过归纳出的函数关系或规则推理并确定相应的类变量值。分类器的质量与分类器构造方法、待分类数据的特性以及训练样本数量等诸多因素有关[1]。而在分类器中一个重要分支是概率分类器，在概率分类器中，首先确定变量间的关系结构，便会得到分类器的参数布局，然后再用训练集中的数据信息依据一定的方法来进行参数估计。贝叶斯分类器便是常见的概率分类器。

贝叶斯方法是模式识别中的一个相对基本的方法，一般在模式识别的应用中会以贝叶斯方法作为起点，当该方法不足以处理问题时，我们便会选择更为复杂的方法，如神经网络、支持向量机等。贝叶斯决策论将分类问题转化为概率问题，故所有的概率都应是从数据中计算或是估计得到的[2]。朴素贝叶斯(Naive Bayes)分类器是贝叶斯方法中的一个代表方法。

经过相似的地质条件和相似的成岩改造得到的沉积物称为储集岩的单元，而岩性识别则是将其分类的过程。在诸多地质研究工作中，岩性识别具有重要的地位。在油气勘探中，岩性识别是一项基础而重要的环节。识别油藏岩石的各种岩性是石油储层特征的主要任务，是储层特征研究、储量计算和地质建模的基础。将贝叶斯方法应用于岩性识别，可以进行计算简单、性能高效的岩性分类。

1 朴素贝叶斯

1.1 贝叶斯方法

贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。我们通过贝叶斯法则的公式(式(1))来介绍这一方法。

(1)

式中：P(c)为类“先验”概率；P(x|c)为样本x相对于类变量c的类条件概率，也称为“似然”；P(x)为用于归一化的“证据”因子。对给定样本x，证据因子P(x)与类变量无关，对所有类别来说都是相同的。因此估计P(c|x)的问题就转化为如何基于训练数据D提供的信息来估计先验P(c)和似然P(x|c)。

类先验概率P(c)表示在样本空间中，每个类的样本所占的比例，根据大数定律，当训练集样本充足时，P(c)的概率值可通过各类样本出现的频率来进行估计。

对类条件概率P(x|c)来说，涉及关于x的所有属性的联合概率，直接根据样本出现的频率来估计会是一个很大的难题。由于很多样本取值在训练集中根本没有出现，但没有在样本中出现并不代表概率值为零，故直接使用频率来估计P(x|c)显然不可行。

1.2 朴素贝叶斯分类器

贝叶斯方法在实际应用中有时会存在样本稀疏等问题，为了解决类似问题，也为了降低模型结构和计算的复杂度，研究者们引入了“属性条件独立性假设”：即对已知类别，假设所有属性相互独立。这就是朴素贝叶斯分类器，即假设每个属性独立地对分类结果发生影响，虽然这个假设在现实情况下过于理想化很难成立，但由于在分类中，首先我们只要将各类变量概率值的排序找出，而并不需要用完全精确的概率值计算；其次在属性之间的依赖关系有时会对所有类别的影响相同，有时这种依赖关系所带来的影响能相互抵销，故朴素贝叶斯分类器的应用往往能够得到较好较准确的结果[3]。

在条件独立性假设下，朴素贝叶斯分类器具有简单的星形结构，如图1所示。可以看出，每个属性结点只有唯一的类父结点，这意味着，当类给定时，属性之间条件独立(式(2))。

图1 朴素贝叶斯结构

(2)

式中：d为属性数目；xi为x在第i个属性上的取值。

对于所讨论的所有类别来说，P(x)都是相同的，故得到如式(3)所示的判别准则。

(3)

即，所判类别为属于赋予先验概率为权重的概率乘积的最大值。

在分类器中，对每个属性条件概率P(xi|c)的估计是首要的计算部分，只有求出条件概率才能进行贝叶斯分类的判别。在本文中，用参数和非参数两种不同的方法来进行概率密度估计，分别为核密度估计和混合高斯模型，再进行对比。

2 核密度估计

在统计学中，核密度估计(KDE)是估计随机变量的概率密度函数的非参数方法。核密度估计是基于有限数据样本进行推理的基本数据平滑问题。在诸如信号处理和计量经济学等领域，它也被称为Parzen-Rosenblatt窗口方法，其表达式见式(4)。

(4)

式中：X1，X2，…Xn为随机变量x的n个样本；h为带宽，也称平滑参数，在核密度估计中具有重要作用；K(·)为核函数，在本文中使用的核函数为高斯核函数，其表达式见式(5)。

(5)

在核密度估计中一个较为重要的影响因素为带宽h的选择，带宽h的选择差异会带来核密度估计结果上的较大差异。带宽h过小会造成核密度估计曲线光滑性差，过于粗糙，会产生一些过拟合的问题；而带宽过大会造成核密度估计曲线过为平滑，从而失去应有的特征细节[4]。

图2为不同带宽的核密度估计曲线。我们可以看出过小和过大的带宽选择都会给概率密度估计造成干扰，只有选择合适的带宽才能更好地拟合概率密度。

图2 不同带宽的核密度估计

常用的确定带宽的方法一般有经验法则，其表达式见式(6)。

(6)

在应用中还有一些确定带宽的方法，例如自适应带宽方法，也称自动带宽选择方法[5]。在本文中我们分别用两种不同的确定带宽的方法，ksdensity简称ksd为用经验法则确定固定带宽的核密度估计，kde为自适应带宽方法，通过局部数据分布确定调整带宽。不同属性的数据分布用两种不同核密度估计方法进行概率密度估计，并作出图像(图3)。

可以看出kde方法作出的图像会产生锯齿形波动的现象，这是由于在自动调节带宽的情况下，有时由于局部数据特性会使得带宽会过小。使得图像过于粗糙，对概率密度的模拟不够准确，不具有普适性。所以我们在文中选择依据经验法则确定带宽的方法进行应用。

3 混合高斯

正如前文所述，在核密度估计的方法中，如何选择带宽h决定了得到的不同的密度估计，如果我们能避免平滑参数的选择，那便会在一定程度上对模型的一些主观性决策有所帮助。在本文中提出的第二个概率密度方法便是混合高斯方法。然而，在通常情况下，当我们消除一个参数时，我们最终需要用另一个参数替换它。在混合高斯方法中，我们将对于带宽的选择转为确定对高斯混合模型个数的选择。

贝叶斯混合高斯模型是一种参数方法，假设概率密度fGMM(x)可以用K个加权的概率密度总和来建模，其中K≪n。单变量混合高斯公式见式(7)。

(7)

式中：φi为第i个项的权重或混合系数；N(x;μi，Σi)为概率密度，即高斯函数，参数由向量μi，Σi表示，即以μi为均值和Σi为协方差矩阵的正态分布。为了确保这是真正的密度，我们必须强加条件φ1+…+φK=1和φi>0为了评估fGMM(x),我们考虑我们的样本点x，找出该点处的组分密度N(x;μi，Σi)的值，并取这些值的加权和。

在参数估计过程中，一般使用EM算法估计参数φi*，μi*和Σi*。EM算法是一种常用的参数估计方法，是一种迭代式算法，相比于梯度下降等优化算法的求解，求和的项数不会随着参数变量的数目以指数级上升，计算较为简单，EM算法是一种非梯度优化方法[6]。

在混合高斯模型中，高斯模型的数量是需要考虑的一个因素，数量过少，会使得拟合不准确，在接下来的工作中造成一定程度的信息缺失；而数量过多，尤其在样本数据有限的情况下，过多的高斯模型会对样本数据造成一定的压力，在EM算法进行参数估计的迭代时，会产生在一定迭代步数内不收敛等一系列问题，虽然该问题可以在编程时通过一些技巧性操作进行解决，但也会造成过拟合等现象使得结果失去准确性[7]。

图3 两种不同的核密度估计方法对比

4 实例分析

本文研究数据来自苏东41-33区块下古气井的89口测井曲线，该区块位于鄂尔多斯盆地苏里格中区与东区的交界处，具有丰富的油气资源。该地区岩性为复杂的碳酸盐岩，主要分为7种岩性，分别是石灰岩、白云质石灰岩、泥质石灰岩、白云岩、灰质白云岩、泥质白云岩和泥岩。同时，针对该研究区块的储层特征，以测井资料中已知岩性地层的数据为基础，根据行业标准最终优选6个对岩性较为敏感的测井曲线属性，有自然伽马(GR)、中子(CNL)、密度(DEN)、声波时差(AC)、光电截面指数(PE)和电阻率(RLLD)。选取的这些测井变量从不同角度能够较好地反映地层不同岩性特点，组合起来作为复杂碳酸盐岩岩性识别综合评价的特征体系，分析其变化特征，总结其在已知确定的关键井主要岩石类型的测井响应特征[1]。

由于选用单一测井数据分析不具有普遍性，因此本次研究数据从整个工区所有测井曲线样本中等概率随机抽取，每种岩性抽取200个样本，共计抽取1 400个岩石数据用于前期数据分析。并且基于前人经验，先对RLLD数据进行了对数处理(log10)，然后对六个测井曲线分别进行去量纲化，即标准化，避免了不同量纲对分类器造成不良影响。将经过上述处理过的数据，用于我们的实例数据分析。

在本文的实例分析中，分别用不同的概率密度估计方法对训练集中数据进行概率密度估计，其中包括前文所介绍的两种方法，核密度估计方法与混合高斯方法，并用单高斯模型对概率密度进行拟合用于本文方法的对照。

由于朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在混合高斯方法中，不同属性间会存在相关性，即协方差矩阵非单位矩阵，随着属性增多，相关性的干扰往往越强，这种相关性会对混合高斯的结果产生影响，使得分类效率降低，于是对6种属性用主成分分析(PCA)进行正交化处理，增强属性的独立性，提高分类的准确率(图4)。

在图4中可以看出，不同属性对于岩性的分类情况，用核密度估计方法中的固定带宽方法作出每种属性不同岩性的概率密度曲线图。从中可以看出，不同的属性对于七种岩性的区分度也不同，在光电截面指数(PE)属性的图中，七种岩性的分布较为独立，重叠部分即相对较少，误判区小；而在自然伽马(GR)属性的图中，七种岩性区分度较低，重叠部分也较多，误判区大。为了更好地对数据的岩性分类，我们将六种不同的测井属性和岩性类别综合起来，构造出朴素贝叶斯框架，用朴素贝叶斯分类器対岩性进行理论较为严密，结果较为准确的分类(图5)。

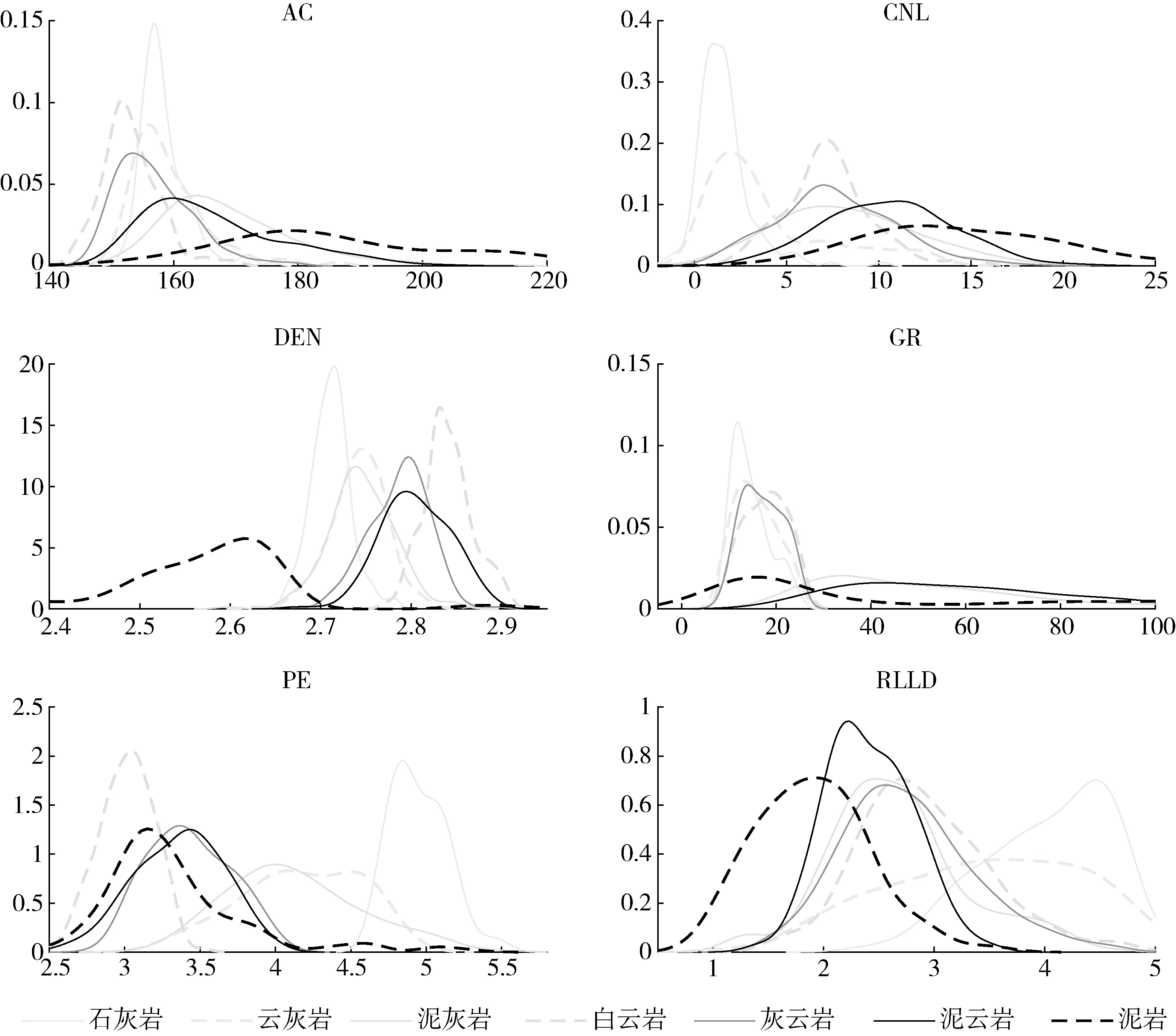
图4 用ksd方法作出的六种属性的岩性分布

图5为核密度估计方法和混合高斯方法对于不同岩性的不同属性的分类数据的概率密度估计的曲线图。其中，七行表示七种不同的岩性，六列表示六种属性。在每个小图中黑色线条表示核密度估计中ksd方法的概率密度估计，浅色实线表示三高斯混合方法(GMM3)的概率密度估记，浅色虚线表示高斯函数的三个成分(comp1-3)。可以看出核密度估计方法和三高斯混合方法的概率密度拟合较为一致，有的类别的属性概率曲线有所不同，峰值、偏度和形状等特征会有不同，但大体上是一致的，而这些概率密度拟合上的不同，造成了分类准确度上的差异，为分类器分类的效果提供了对比。

在测试集中我们选用该区块下古气井的89口完整测井曲线数据，对训练结果进行测试。由于测试的样本较多，可以避免结果的偶然性，使结果具有一定的代表性和普遍性。在实例分析中我们用朴素贝叶斯分类器对测试集中的数据进行岩性分类，并进行分类准确率对比。

将该89口井测试出的准确率结果用折线图表示，横坐标顺序由小图中黑色实线所代表模型的训练准确率由低到高排列决定，不同颜色形态的折线代表不同的概率密度估计方法，如图6所示。

可以看出，图6(a)中两种不同确定带宽的核密度估计方法kde和ksd准确率几乎持平，但由于前文中所述的自适应带宽方法拟合出的概率曲线过于粗糙的问题，选择使用ksd方法即由经验法则确定带宽；而对于单高斯和混合三高斯模型的对比，由图6(b)中可以看出，三高斯混合模型(虚线条)的准确率明显高于单高斯模型(实线条)，只有极少数准确率较低；而在图6(c)中可以看出用核密度估计方法(浅色线条)及三高斯混合模型(虚线条)的概率密度估计所得出的分类准确率大体上比单高斯模型(深色实线条)更高，仅在少数口井的测试中准确率低于单高斯模型。而在前两种方法的比较中，三高斯混合模型较核密度估计方法来说具有相对较高的测试准确率，在图中表示即为虚线条在浅色线条之上的部分较多。

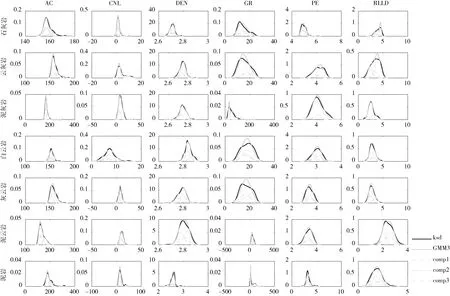
图5 不同方法概率密度估计曲线图

图6 不同方法准确率折线图

5 结 论

1) 在岩性分类的方法应用中，朴素贝叶斯方法在分类技术中占据一席之地，其数学理论严谨，分类效率较为稳定，相比于其他方法对参数需求较小，而且易于理解，模型架构简单易行，是一种较为常用，基础的分类方法。这种方法对测井曲线所能获得的多种属性进行综合分类，是多元统计学习在地质矿产储层特征研究中较为广泛使用并且有效的方法。

2) 对概率密度估计方法的选择在朴素贝叶斯分类器中是一个影响较大的因素。本文的朴素贝叶斯分类器应用中，用参数方法的混合高斯概率密度估计方法用于估计条件概率的分类效果最好，而注意在一般数据量足够的情况下，需要三个以上的混合模型才能达到相比核密度估计较高的准确率。在本文的训练数据的条件下通过对比选择了三高斯混合模型的结果较好，但是对于不同环境下的样本数据，也需要依据样本数据的特征进行分析并判断选择一个合适的模型数量或者建模方法。

3) 在实际应用中，混合高斯模型在系统的计算负载方面提供了一定的优势。在概率密度估计方法中，有两个需要考虑的因素：需要储存的信息量对计算造成的负担，以及在某一点上为获得概率密度估计所需的计算工作量。在核密度估计方法中，我们须保留所有数据点，计算以每个样本点为中心的多个核的加权和，需多次计算核值，在多变量的情况下计算负荷会更大[8]。随着越来越多地使用大量、高维的数据集，计算工作量和使用核密度估计必须存储的信息量也越来越大。用混合高斯方法估计概率密度函数，相较于其他的密度估计方法尤其是核密度估计法，需要相对较少的计算机存储空间及计算量，所以混合高斯方法不论在准确性方面还是计算复杂度方面，均更适合于实际应用中与朴素贝叶斯分类器相结合。

4) 由于朴素贝叶斯的属性条件独立性假设较为理想化，对于实际应用的数据属性一般具有或多或少的相关性[9]，所以该方法存在一定的不准确性，故半朴素贝叶斯分类器和贝叶斯网等分类方法将成为进一步研究的目标。